
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазоманипулированных сигналовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Будем рассматривать сложные (псевдошумовые, псевдослучайные, с расширенным спектром) амплитудно-фазо-манипулированные сигналы (АФМ-сигналы), являющиеся последовательностями
Здесь
Часто вместо используют другую запись для сложного сигнала:
где
- комплексная огибающая радиосигнала Для другого сложного АФМ-сигнала с номером
Наиболее простыми для практического использования являются сигналы, для которых Комплексная огибающая (1.3) ФМ-сигнала является вещественной
и полностью определяется кодовой последовательностью
Автокорреляционная функция (АКФ) радиосигнала
где Аналогичным образом определяется взаимная корреляционная функция двух сложных сигналов
Известно также, что функции и могут быть вычислены по комплексным огибающим этих сигналов:
где
есть комплексная огибающая ВКФ. Здесь В частности для исследуемых в данной работе ФМ-сигналов
Для любых допустимых значений
где
треугольная функция, отличная от нуля только на интервале
и является вещественной функцией. Введя обозначение
В соответствии с комплексная огибающая ВКФ двух ФМ-сигналов
которые могут принимать положительные и отрицательные значения. На основании и для взаимной корреляционной функции двух радиосигналов
В частном случае при В формуле каждое слагаемое имеет форму треугольного импульса. Слагаемое с номером 2 .Напишите определение взаимокорреляционной функции сигналов s (n) и x (n) Взаимная корреляционная функция определяет временную связь двух сигналов во времени. Если сигналы не зависимы друг от друга, их корреляционная функция равна нулю. Чем шире корреляционная функция, тем большая степень связи двух сигналов друг с другом. Взаимная корреляционная функция определяется соотношением
Пример получения взаимной корреляционной функции показан на рис.1. Значение корреляционной функции в любой момент x определяется площадью пересечения функций
Рис. 1 Взаимная корреляционная функция не обязательно симметрична и её максимум может оказаться не в точке x=0.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 элементарных радиоимпульсов с прямоугольной огибающей, длительностью
элементарных радиоимпульсов с прямоугольной огибающей, длительностью  , одинаковой частотой несущего колебания
, одинаковой частотой несущего колебания  и разными амплитудами и начальными фазами:
и разными амплитудами и начальными фазами:
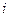 - номер сложного сигнала,
- номер сложного сигнала, 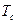 длительность этого сигнала,
длительность этого сигнала,  и
и  - амплитуда и начальная фаза
- амплитуда и начальная фаза  -го элементарного символа
-го элементарного символа 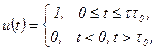 определяет форму огибающей элементарного символа.
определяет форму огибающей элементарного символа. ,
,
 .
. комплексную огибающую также можно записать в форме, аналогичной:
комплексную огибающую также можно записать в форме, аналогичной: ,
,  .
.
 ,
, 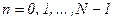 , т.е. амплитуды элементарных символов одинаковы, а фазы принимают лишь два возможных значения 0 и
, т.е. амплитуды элементарных символов одинаковы, а фазы принимают лишь два возможных значения 0 и 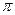 . В этом случае комплексные амплитуды элементарных символов
. В этом случае комплексные амплитуды элементарных символов  оказывается вещественными, поскольку
оказывается вещественными, поскольку  и
и  . Здесь
. Здесь 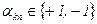 . Такие сигналы называют сложными фазоманипулированными (ФМ-сигналами).
. Такие сигналы называют сложными фазоманипулированными (ФМ-сигналами). ,
, 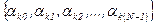 .
. ,
,  ,.
,.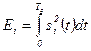 - энергия сигнала.
- энергия сигнала. :
: ,
,  ,
, ,
,  ,
,  .
.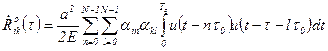 ,
,  .
. и
и 

 и имеющая максимальное значение 1 при
и имеющая максимальное значение 1 при  . В результате комплексная огибающая ВКФ двух ФМ-сигналов с расширенным спектром принимает вид:
. В результате комплексная огибающая ВКФ двух ФМ-сигналов с расширенным спектром принимает вид:
 , меняя порядок суммирования и учитывая, окончательно получаем:
, меняя порядок суммирования и учитывая, окончательно получаем: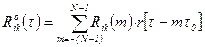 .
.
 .
. из, и получаем автокорреляционную функцию радиосигнала.
из, и получаем автокорреляционную функцию радиосигнала. называется основным (главным) пиком. Он имеет максимальное значение, равное 1. Импульсы АКФ с номерами
называется основным (главным) пиком. Он имеет максимальное значение, равное 1. Импульсы АКФ с номерами  , называются боковыми пиками.
, называются боковыми пиками.
 и сдвинутой копии
и сдвинутой копии  .
.



