
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напишите определение автокорреляционной функции сигнала s(t ).Содержание книги
Поиск на нашем сайте Напишите определение автокорреляционной функции сигнала s(t). Автокорреляционная функция — зависимость взаимосвязи между функцией (сигналом) и ее сдвинутой копией от величины временного сдвига. Для детерминированных сигналов автокорреляционная функция (АКФ) сигнала {\displaystyle f(t)} {\displaystyle \Psi (\tau)=\int _{-\infty }^{\infty }f(t)f^{*}(t-\tau)\mathrm {d} t} и показывает связь сигнала (функции Свойства автокорреляционной функции. 1. Если
Данное выражение легко доказать, сделав следующую замену вида Тогда. 3.При любом
Данное выражение вытекает из неравенства Коши.
Это свойство еще раз показывает, что с увеличением времени 4.Данное свойство вытекает из предыдущих. Если проанализировать АКФ относительно энергии сигнала Пределы изменения АКФ от –1, до1 и с возрастанием Геометрический смысл автокорреляционной функции заключается в определении площади пересечения функции
Рис. 2 Изменяя время сдвига x до тех пор, пока сигнал и его копия перестанут пересекаться (в данном случае
а в свою очередь полная энергия сигнала равна
Таким образом, максимум автокорреляционной функции определяет полную энергию сигнала. При увеличении сдвига x АКФ убывает до нуля. Автокорреляционные и взаимно-корреляционные функции Приведите выражение для начального момента порядка n случайной величины X с характеристической функцией Q(v).
4.Какое устройство осуществляет отображение информационной последовательности { }n a во множество элементарных сигналов { ()} m s t? Каково должно быть число элементарных сигналов M для передачи k бит одним элементарным сигналом? Демультиплексор M=2^k или k=log2(M) Нарисуйте фазовое созвездие сигнала ФМн-8 (PSK-8). Напишите около каждой точки фазового созвездия значения информационных битов, передаваемые соответствующим элементарным сигналом (отображение битов в элементарные сигналы осуществите по Грею)
Пусть сигнал S(t) со скоростью передачи информационных символов R и модуляцией PSK-8 подвергается расширению типа DSSS с использованием ПСП X(t) длиной L. Чему будет равна чиповая скорость сигнала S(t), расширенного последовательностью X(t)? Чему будет равна скорость передачи информации?
Бинарная фазовая модуляция В общем случае формирование фазоманипулированного сигнала, или как его еще называют BPSK-сигнала (binary phase shift keying), происходит с помощью фазового модулятора, представленном на рисунке 3.
Рисунок 3 – Формирование ФМ-сигнала на основе фазового модулятора
На вход модулятора поступает ШПС, т.е. произведение информационной последовательности и ПСП, далее этот сигнал умножается на значение π, после чего поступает на вычислитель синфазной I(t) и квадратурной Q(t) составляющих сигнала. Синфазная и квадратурная составляющая сигнала переносятся на несущую частоту, и результаты модулирования этих составляющих поступают на сумматор, на выходе которого мы получим BPSK-сигнал. Поскольку S(t) принимает только значения равные 0 и 1, то синфазная I(t) и квадратурная Q(t) компоненты комплексной огибающей
Тогда BPSK-сигнал можно записать:
а структурную схему модулятора можно упростить, как это показано на рисунке 4.
Рисунок 4 – Упрощенная структурная схема BPSK модулятора
Поясняющие графики формирователя BPSK-сигнала показаны на рисунке 5.
Рисунок 5 – Поясняющие графики BPSK модулятора
Представим некий ШПС S(t) (рисунок 5а), который умножается на несущее колебание M-последовательности Выше было упомянуто, что оптимальными для расширения спектра сигнала являются последовательности максимальной длины или М-последовательностями. Такие последовательности формируются с помощью цифровых автоматов, основным элементом которых является сдвигающий регистр с ячейками памяти Т1, Т2, …, Тk (рисунок 2).
Тактовые импульсы поступают на все ячейки одновременно с периодом
В соответствии с значение символа Если принять содержание ячеек регистра сдвига за исходное состояние, то через Структурную схему автомата, формирующего М-последовательности, принято задавать характеристическим многочленом:
в котором всегда – если – если Например, при
Цифровой автомат, формирующий М-последовательность с характеристическим полиномом В сотовых системах второго поколения с технологией кодового разделения каналов (стандарт IS-95) используются М-последовательности с длиной регистров сдвига Преимущества · Гибкое распределение ресурсов. При кодовом разделении нет строгого ограничения на число каналов. С увеличением числа абонентов постепенно возрастает вероятность ошибок декодирования, что ведёт к снижению качества канала, но не к отказу обслуживания. · Более высокая защищённость каналов. Выделить нужный канал без знания его кода весьма трудно. Вся полоса частот равномерно заполнена шумоподобным сигналом. · Телефоны CDMA имеют меньшую пиковую мощность излучения и потому позволяют более экономно расходовать батарею. Замирания сигнала Сигнал на радио интерфейсе системы сотовой связи редко когда распространяется по прямой. На пути распространения обычно попадаются различные препятствия, которые ведут к отражениям сигнала и изменению его траектории. В результате может сложиться ситуация когда к приемнику будут поступать не одна а сразу несколько сдвинутых по времени копий исходного сигнала с разными амплитудами. Причем энергия исходного сигнала будет распределена между копиями неравномерно. Это так называемое явление многолучевого распространения сигнала. Само по себе это явление не ведет к большим проблемам, т.к. существуют достаточно эффективные методы борьбы, например, Rake-приемник. Однако может сложиться ситуация когда две копии сигнала придут в противофазе. Это означает, что копия сигнала может задержаться на промежуток времени кратный периоду сигнала. В таком случае два луча сигнала могут сложиться в приемнике и нейтрализовать друг друга. Если окажется, что эти два луча в сумме несли весомую энергию сигнала, то это может привести к увеличению числа ошибок и снижению качества канала связи. Это явление получило название "замирания" сигнала, т.е. сигнал вроде как перестает на время поступать между источником и приемником.
Замирания сигналов Выделяют две основные разновидности замираний в зависимости от эффекта оказываемого ими и их причины: быстрые и медленные замирания. Медленные замирания вызваны, как правило, плохими метеоусловиями и существуют достаточно эффективные методы борьбы с ними. Быстрые замирания вызваны преимущественно движением приемника (источника) или препятствиями близкорасположенными с получателем сигнала. Этот вид замираний частотно селективен, т.е. изменение частоты, на которой ведется передача, может или снизить этот эффект, или полностью его убрать. Таким образом, замирания сигнала – это одна из самых важных проблем в сотовой связи. Однако многолетний опыт и большой объем наработок в области сотовой связи позволяют в настоящее время достаточно эффективно бороться с замираниями.
Системы DS-CDMA Один из наиболее широко применяемых сегодня на практике способов формирования ШПС, который называется методом прямого расширения спектра путем фазовой модуляции несущей определенной кодовой последовательности (DS-SS - Direct Sequence Spread Spectrum), был изобретен американскими специалистами Дж. Г. Грином и М. Г. Никольсоном в 1957 г. Ими был предложен метод построения бинарной кодовой последовательности с хорошими корреляционными свойствами. Позже было выполнено значительное число работ, посвященных синтезу подобных псевдослучайных последовательностей с помощью регистров сдвига. К первым теоретическим разработкам в этом направлении относятся исследования С. Голомба (1955 г.) и Н. Цирлера (1959 г.) Метод прямой последовательности (DS) - это модуляция несущей информационным сигналом с последующей модуляцией широкополосным расширяющим сигналом. В качестве широкополосного сигнала, как правило, используются случайные или псевдослучайные последовательности (ПСП). Разница между ними заключается в следующем: случайная последовательность непредсказуема и может быть описана только в статистическом смысле. А ПСП на самом деле не является случайной - это детерминированная периодическая последовательность, воспринимаемая передатчиком и приемником. Тому, кто не знаком с данным видом ПСП, она покажется абсолютно случайной. Такие системы нашли свое применение в системах подвижной сотовой связи (например, стандарт IS-95), в фиксированном абонентском радиодоступе (FBWA) и других системах связи. Системы FH-CDMA Идея реализации скачкообразной перестройки частоты, или многочастотной модуляции с кодовым управлением синтезатором частот, впервые возникла при построении систем военной связи. Системы FH-CDMA обеспечивают высокую помехозащищенность и низкую вероятность перехвата.
Системы TH-CDMA Метод расширения спектра с временной перестройкой TH-CDMA состоит в следующем. Информационный сигнал сжимается во времени и передается в виде коротких пакетов в случайные моменты времени, определяемые специальной кодовой последовательностью ПСП. Временная ось при использовании TH-CDMA сегментируется на кадры длительностью Т, каждый из которых состоит из М временных интервалов длительностью Т/М. В течение одного кадра информация передается только в одном из временных интервалов (и этим TH-CDMA напоминает способ импульсной временной модуляции). Очевидно, что ширина полосы частот, необходимая для реализации TH-CDMA, должна быть гораздо больше, чем при DS-CDMA, а конкретно - в М раз. Снижение взаимных помех в системах TH-CDMA достигается за счет выделения абонентам различных временных интервалов. Корректирующие коды, конечно, повышают помехоустойчивость, но не гарантируют правильного восстановления полезного сигнала. Защита систем TH-CDMA от внешних помех обеспечивается самой основой метода. Поскольку сигнал TH-CDMA сжат во времени, т.е. излучается лишь в интервале, равном 1/В (В -база сигнала), при приеме он обрабатывается в течение такого же короткого промежутка времени, поэтому мешающий сигнал будет уменьшен также в В раз. Что же касается защиты от перехвата, то, хотя частота, на которой передаются данные, и является фиксированной, сам момент начала передачи неизвестен, а потому приемнику перехвата трудно определить начало и конец этой передачи, а самое главное - выяснить, какому абоненту принадлежит излучаемый сигнал. Данный метод наиболее предпочтителен в тех системах, где ограничена средняя, а не пиковая мощность передатчика. Метод прямой последовательности для расширения спектра (DSSS - англ. d irect s equence s pread s pectrum) — широкополосная модуляция с прямым расширением спектра, является одним из трёх основных методов расширения спектра, используемых на сегодняшний день (см. методы расширения спектра). Это метод формирования широкополосного радиосигнала, при котором исходный двоичный сигнал преобразуется в псевдослучайную последовательность, используемую для модуляции несущей. Используется в сетях стандарта IEEE 802.11 и CDMA для преднамеренного расширения спектра передаваемого импульса. Метод прямой последовательности (DSSS) можно представить себе следующим образом. Вся используемая «широкая» полоса частот делится на некоторое число подканалов — по стандарту 802.11 этих подканалов 11. Каждый передаваемый бит информации превращается, по заранее зафиксированному алгоритму, в последовательность из 11 бит, и эти 11 бит передаются как бы одновременно и параллельно (физически сигналы передаются последовательно), используя все 11 подканалов. При приёме, полученная последовательность бит декодируется с использованием того же алгоритма, что и при её кодировке. Другая пара приёмник-передатчик может использовать другой алгоритм кодировки — декодировки, и таких различных алгоритмов может быть очень много. Первый очевидный результат применения этого метода — защита передаваемой информации от подслушивания («чужой» DSSS-приёмник использует другой алгоритм и не сможет декодировать информацию не от своего передатчика). При этом сильно уменьшается отношение уровня передаваемого сигнала к уровню шума, (то есть случайных или преднамеренных помех), так что передаваемый сигнал уже как бы неразличим в общем шуме. Но благодаря его 11-кратной избыточности принимающее устройство все же сумеет его распознать. Еще одно чрезвычайно полезное свойство DSSS-устройств заключается в том, что благодаря очень низкому уровню мощности своего сигнала они практически не создают помех обычным радиоустройствам (узкополосным большой мощности), так как эти последние принимают широкополосный сигнал за шум в пределах допустимого. И наоборот — обычные устройства не мешают широкополосным, так как их сигналы большой мощности «шумят» каждый только в своем узком канале и не могут целиком заглушить весь широкополосный сигнал. Использование широкополосных технологий дает возможность использовать один и тот же участок радиоспектра дважды — обычными узкополосными устройствами и «поверх них» — широкополосными. В каждый передаваемый информационный бит (логический 0 или 1) встраивается последовательность так называемых чипов. Если информационные биты — логические нули или единицы — при потенциальном кодировании информации можно представить в виде последовательности прямоугольных импульсов, то каждый отдельный чип — это тоже прямоугольный импульс, но его длительность в несколько раз меньше длительности информационного бита. Последовательность чипов представляет собой последовательность прямоугольных импульсов, то есть нулей и единиц, однако эти нули и единицы не являются информационными. Поскольку длительность одного чипа в n раз меньше длительности информационного бита, то и ширина спектра преобразованного сигнала будет в n раз больше ширины спектра первоначального сигнала. При этом и амплитуда передаваемого сигнала уменьшится в n раз. Чиповые последовательности, встраиваемые в информационные биты, называют шумоподобными кодами (PN-последовательности), что подчеркивает то обстоятельство, что результирующий сигнал становится шумоподобным и его трудно отличить от естественного шума. Используемые для уширения спектра сигнала чиповые последовательности должны удовлетворять определённым требованиям автокорреляции. Под термином автокорреляции в математике подразумевают степень подобия функции самой себе в различные моменты времени. Если подобрать такую чиповую последовательность, для которой функция автокорреляции будет иметь резко выраженный пик лишь для одного момента времени, то такой информационный сигнал возможно будет выделить на уровне шума. Для этого в приёмнике полученный сигнал умножается на ту же чиповую последовательность, то есть вычисляется автокорреляционная функция сигнала. В результате сигнал становится опять узкополосным, поэтому его фильтруют в узкой полосе частот и любая помеха, попадающая в полосу исходного широкополосного сигнала, после умножения на чиповую последовательность, наоборот, становится широкополосной и обрезается фильтрами, а в узкую информационную полосу попадает лишь часть помехи, по мощности значительно меньшая, чем помеха, действующая на входе приёмника (если не используется приёмник с алгоритмом Боцмана). Циклический префикс Наверх Одним из главных преимуществ метода OFDM является его устойчивость к эффекту многолучевого распространения. Для того чтобы избежать межсимвольных искажений, перед каждым OFDM-символом вводится защитный интервал, называемый циклическим префиксом. Циклический префикс представляет собой копию фрагмента полезного сигнала, таким образом некоторый фрагмент начала символа OFDM такой же, как и в конце символа. Это гарантирует сохранение ортогональности поднесущих (но только в том случае, если отраженный сигнал при многолучевом распространении задержан не больше, чем на длительность циклического префикса). Кроме того, циклический префикс позволяет выбрать окно для преобразования Фурье в любом месте временного интервала символа (рисунок 4).
Рисунок 4. Циклический префикс. Структура кадра OFDM. При выборе структуры кадра необходимо обеспечить, во-первых, быстрое вхождение в синхронизм демодулятора цифрового телевизора, с тем чтобы не вызвать чувства раздражения у телезрителей в моменты переключения телевизора с одной программы на другую. Во-вторых, формат кадра OFDM должен быть согласован с форматом транспортного пакета MPEG-2 (длительность пакета 204 байта), с тем чтобы взаимные преобразования этих форматов в модеме могли быть выполнены простыми техническими средствами. В результате учета этих требований в стандарте OFDM была принята двухступенчатая структура передачи данных в виде супер-кадра, состоящего из 4 кадров OFDM. При этом в одном супер-кадре содержится целое число транспортных пакетов MPEG-2, что позволяет производить взаимные преобразования форматов транспортных пакетов и супер-кадра OFDM без введения в модем OFDM стаффинг-синхронизации. В то же время наличие в супер-кадре 4 кадров повышает в 4 раза скорость передачи сигналов синхронизации, за счет чего обеспечивается приемлемое время вхождения в синхронизм демодулятора телевизора.
Рисунок 1. Система MIMO 4х4 с пространственным мультиплексированием
Итак, рассмотрим данную схему более подробно. Передаваемое сообщение представляет собой поток двоичных символов – бит. Модулятор осуществляет изменение параметров несущего сигнала в соответствии с изменениями передаваемого (информационного) сигнала. Например, один символ QPSK переносит 2 бита информации, 16QAM – 4 бита, 64 QAM – 6 бит. Далее комплексные символы демультиплексируются на Модель системы описывается уравнением:
где Модель MIMO канала – это есть канальная матрица коэффициентов передачи по каждой трассе распространения. Характеристики данной матрицы отражают условия распространения в MIMO-канале. Если бы шумы в (1) отсутствовали бы, то по вектору наблюдений Y можно было бы точно определить вектор передаваемых символов Х, если только определитель матрицы Н не был бы равен нулю в точности. При наличии шумовых возмущений, для получения близких к точным решений, факта отличия от нуля определителя матрицы Н уже не достаточно. Как это следует из теории матриц для этого необходимо еще, чтобы определенный параметр матрицы – число обусловленности – был бы не слишком большим. Этот параметр для различных матриц лежит в пределах от 1 до ∞ и отражает устойчивость системы вида
где Специально для данной лабораторной работы была написана упрощенная модель многолучевого канала связи MIMOChannel.m. Данная модель представляет собой функцию MatLab, с определенными входными параметрами. Она построена на вариации числа отражательных поверхностей, расположенных между приемной и передающей частями. На рисунке 2 приведена схема отражательной модели канала. Все лучи пришедшие на прием могут складываться по-разному в зависимости от фаз каждого из лучей. Фаза каждого пришедшего луча зависит от пройденного им расстояния. Таким образом, увеличивая число отражающих поверхностей, мы увеличиваем число лучей по каждой трассе распространения, тем самым создавая условия для более глубоких замираний сигналов на каждой трассе.
Рисунок 2. Схематичное изображение отражательной модели
Пройдя через канал, наши сигналы детектируются и демодулируются в групповом приемнике. В данной лабораторной работе используется приемник максимального правдоподобия, ищущий самую близкую комбинацию из всех возможных к принятому созвездию сигналов путем минимизации евклидовой нормы. Приемник максимального правдоподобия описывается следующей формулой:
Одним из пунктов данной лабораторной работы является получение гистограмм распределения огибающей канала по определенной трассе (между конкретной передающей и конкретной приемной антеннами). Беспроводные каналы, в отличие от проводных, показывают непостоянное поведение амплитуды сигнала из-за наличия в каналах замираний или фэйдингов (от англ. fading – замирание). Основной причиной замираний являются многочисленные переотражения переданного в эфир сигнала. Замирания являются причиной изменения мощности принимаемого сигнала во времени, делая извлечение информации из принятого сигнала затруднительным. Рисунок 2. Схема работы пространственно-временного блочного кодирования Аламаути 2x1
Обработка на приемной стороне в схеме Аламаути 2х1 производится в блоке обработки следующим образом. В первый временной интервал принятый сигнал описывается уравнением
Во второй временной слот принятый сигнал описывает уравнением
Здесь
Для определения передававшихся символов необходимо выделить сигналы | |
|
| Поделиться: |

 определяется интегралом:
определяется интегралом:
 {\displaystyle \;f(t)}) с копией самого себя, смещённого на величину {\displaystyle \tau }
{\displaystyle \;f(t)}) с копией самого себя, смещённого на величину {\displaystyle \tau }  . Звездочка означает комплексное сопряжение
. Звездочка означает комплексное сопряжение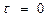 , то
, то  Автокорреляционная функция при расстройке τ =0 принимает свое максимальное и положительное значение, равное энергии самого сигнала.
Автокорреляционная функция при расстройке τ =0 принимает свое максимальное и положительное значение, равное энергии самого сигнала. 2.Автокорреляционная функция
2.Автокорреляционная функция  является четной функцией.
является четной функцией. .
. (2)
(2) модуль автокорреляционной функции не превосходит энергии сигнала.
модуль автокорреляционной функции не превосходит энергии сигнала. .
. .
. АКФ сигнала должна уменьшаться. Ее максимум находится в точке
АКФ сигнала должна уменьшаться. Ее максимум находится в точке  и равен энергии сигнала.
и равен энергии сигнала. , то максимальное значение АКФ равно ±1, а при τ > tи характеристика BU (τ) будет принимать нулевое значение.
, то максимальное значение АКФ равно ±1, а при τ > tи характеристика BU (τ) будет принимать нулевое значение.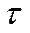 она затухает.
она затухает. и её копии, сдвинутой на время x (Рис.2)
и её копии, сдвинутой на время x (Рис.2)
 ), получим АКФ
), получим АКФ  . Очевидно, что при изменении знака сдвига при одинаковой его величине функция автокорреляции одинакова, т.е.
. Очевидно, что при изменении знака сдвига при одинаковой его величине функция автокорреляции одинакова, т.е.  , что говорит о четном её характере. Ясно, что при x=0 автокорреляционная функция имеет максимум, при этом
, что говорит о четном её характере. Ясно, что при x=0 автокорреляционная функция имеет максимум, при этом



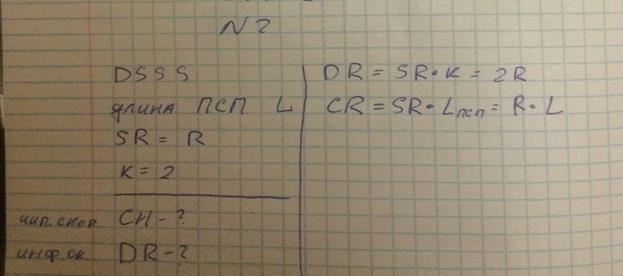

 BPSK-сигнала равны:
BPSK-сигнала равны:



 , в данном примере
, в данном примере  , (рисунок 5б) и получаем BPSK-сигнал со скачком фазы на
, (рисунок 5б) и получаем BPSK-сигнал со скачком фазы на 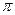 рад (рисунок 5в).
рад (рисунок 5в). Рисунок 2 – Цифровой автомат формирования М-последовательности
Рисунок 2 – Цифровой автомат формирования М-последовательности , передвигая за один такт хранящиеся в этих ячейках символы в соседние справа ячейки. Обозначим буквами
, передвигая за один такт хранящиеся в этих ячейках символы в соседние справа ячейки. Обозначим буквами  символы, хранящиеся в соответствующих ячейках на
символы, хранящиеся в соответствующих ячейках на  -ом такте.
-ом такте.  - символ на входе первой ячейки; значение этого символа формируется с помощью линейного рекуррентного соотношения
- символ на входе первой ячейки; значение этого символа формируется с помощью линейного рекуррентного соотношения
 в ячейке с номером
в ячейке с номером  умножается на коэффициент
умножается на коэффициент  и складывается с остальными аналогичными произведениями. Как символы
и складывается с остальными аналогичными произведениями. Как символы  , то символ ячейки
, то символ ячейки  в формировании значения суммы не участвует.
в формировании значения суммы не участвует. тактов это состояние вновь будет иметь место. Если при этом регистрировать последовательность символов
тактов это состояние вновь будет иметь место. Если при этом регистрировать последовательность символов  регистра сдвига зависит от числа и расположения отводов. Для каждого значения
регистра сдвига зависит от числа и расположения отводов. Для каждого значения  .
. (1.16)
(1.16) ,
, 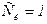 . В табл. 1 для
. В табл. 1 для  указаны наборы значений коэффициентов этого полинома, определяющих последовательности максимальной длины. Знание вектора
указаны наборы значений коэффициентов этого полинома, определяющих последовательности максимальной длины. Знание вектора  позволяет однозначно указать структуру цифрового автомата, формирующего соответствующую полиному (1.16) М-последовательность:
позволяет однозначно указать структуру цифрового автомата, формирующего соответствующую полиному (1.16) М-последовательность: , то выход ячейки с номером
, то выход ячейки с номером  , то выход ячейки с номером
, то выход ячейки с номером  векторам
векторам 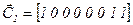 и
и  соответствуют характеристические полиномы:
соответствуют характеристические полиномы: ,
,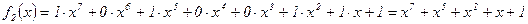 .
. , имеет отводы от ячеек регистра с номерами 6 и 7, а с характеристическим полиномом
, имеет отводы от ячеек регистра с номерами 6 и 7, а с характеристическим полиномом  - 2, 5, 6, 7. Обе последовательности имеют длину
- 2, 5, 6, 7. Обе последовательности имеют длину  .
. (для расширения спектра сигналов и идентификации базовых станций сети) и
(для расширения спектра сигналов и идентификации базовых станций сети) и  (длинный код для скремблирования и идентификации подвижных станций)
(длинный код для скремблирования и идентификации подвижных станций)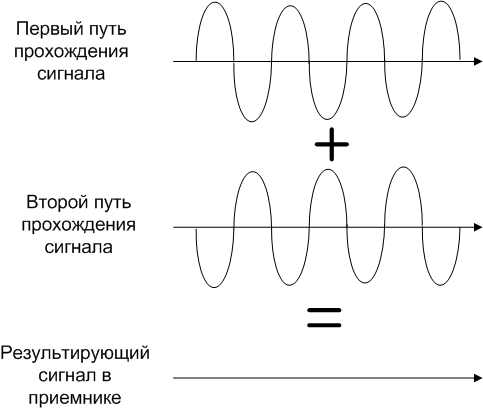

 Принцип скачкообразной перестройки частоты в CDMA-системах воплощается следующим образом. Любой бит передается в виде комбинации из N частот, где N - размерность базиса частот, причем на каждой частоте передается своя псевдослучайная последовательность (ПСП). В течение заданного временного интервала Т несущая остается неизменной, а по его истечении она скачкообразно изменяется. Алгоритм переключения частоты несущей для каждого абонента индивидуален, благодаря чему возможна одновременная работа большого числа абонентов в общей полосе частот. Полный набор используемых частот может быть достаточно велик, однако в каждый заданный алгоритмом интервал времени мобильная станция излучает только на одной частоте. По сравнению с классическим методом расширения спектра прямой последовательностью DS, в соответствии с которым сигнал передается в широкой полосе частот и имеет малый уровень мощности, при использовании FH-CDMA мощность излучения сигнала гораздо выше, а занимаемый в эфире участок спектра значительно уже. Это позволяет обеспечить лучшую, чем в системах DS-CDMA, защиту от узкополосных помех. При наличии широкого набора рабочих частот вероятность одновременной передачи информации от двух абонентов на одной и той же частоте достаточно мала. Отсюда вытекают и главные достоинства технологии FH-CDMA: более высокая помехоустойчивость и меньшая чувствительность к разбросу мощностей мобильных станций. Кроме того, системам на базе FH-CDMA не нужен сплошной участок спектра: изменяя алгоритм перестройки, можно исключить из спектра те частоты, работа на которых запрещена.
Принцип скачкообразной перестройки частоты в CDMA-системах воплощается следующим образом. Любой бит передается в виде комбинации из N частот, где N - размерность базиса частот, причем на каждой частоте передается своя псевдослучайная последовательность (ПСП). В течение заданного временного интервала Т несущая остается неизменной, а по его истечении она скачкообразно изменяется. Алгоритм переключения частоты несущей для каждого абонента индивидуален, благодаря чему возможна одновременная работа большого числа абонентов в общей полосе частот. Полный набор используемых частот может быть достаточно велик, однако в каждый заданный алгоритмом интервал времени мобильная станция излучает только на одной частоте. По сравнению с классическим методом расширения спектра прямой последовательностью DS, в соответствии с которым сигнал передается в широкой полосе частот и имеет малый уровень мощности, при использовании FH-CDMA мощность излучения сигнала гораздо выше, а занимаемый в эфире участок спектра значительно уже. Это позволяет обеспечить лучшую, чем в системах DS-CDMA, защиту от узкополосных помех. При наличии широкого набора рабочих частот вероятность одновременной передачи информации от двух абонентов на одной и той же частоте достаточно мала. Отсюда вытекают и главные достоинства технологии FH-CDMA: более высокая помехоустойчивость и меньшая чувствительность к разбросу мощностей мобильных станций. Кроме того, системам на базе FH-CDMA не нужен сплошной участок спектра: изменяя алгоритм перестройки, можно исключить из спектра те частоты, работа на которых запрещена.
 Структура кадра OFDM показана на рис. 7. Кадр состоит из 68 символов OFDM, которым присвоены номера от 0 до 67. Длительность кадра равна TF=68TS, а значения TS (длительности информационных символов) для различных режимов работы приведены в табл.1. Кадр содержит для режимов модуляций 8К и 2К, соответственно, 6817 и 1705 несущих.
Для работы приемного устройства необходимо совместно с информационными символами передавать опорные сигналы, во-первых, сигналы для фазовой автоподстройки опорных частот демодулятора, во-вторых, — сигналы тактовой синхронизации функциональных блоков демодулятора, в-третьих, — сигналы для оценки состояния эфирного радиоканала, в-четвертых, — сигналы управления демодулятором, содержащие информацию о используемых режимах модуляции. Для этих целей в каждом символе OFDM для режимов модуляции 8К и 2К выделено, соответственно, 769 и 193 опорных несущих, которые по сравнению с информационными несущими передаются с повышенной на 2,5 дБ мощностью.
Для фазовой автоподстройки опорной сетки когерентных частот демодулятора [8] используются так называемые фиксированные опорные несущие, частотные позиции которых в каждом символе OFDM постоянны.
Структура кадра OFDM показана на рис. 7. Кадр состоит из 68 символов OFDM, которым присвоены номера от 0 до 67. Длительность кадра равна TF=68TS, а значения TS (длительности информационных символов) для различных режимов работы приведены в табл.1. Кадр содержит для режимов модуляций 8К и 2К, соответственно, 6817 и 1705 несущих.
Для работы приемного устройства необходимо совместно с информационными символами передавать опорные сигналы, во-первых, сигналы для фазовой автоподстройки опорных частот демодулятора, во-вторых, — сигналы тактовой синхронизации функциональных блоков демодулятора, в-третьих, — сигналы для оценки состояния эфирного радиоканала, в-четвертых, — сигналы управления демодулятором, содержащие информацию о используемых режимах модуляции. Для этих целей в каждом символе OFDM для режимов модуляции 8К и 2К выделено, соответственно, 769 и 193 опорных несущих, которые по сравнению с информационными несущими передаются с повышенной на 2,5 дБ мощностью.
Для фазовой автоподстройки опорной сетки когерентных частот демодулятора [8] используются так называемые фиксированные опорные несущие, частотные позиции которых в каждом символе OFDM постоянны.
 Всего для этой цели в режимах 8К и 2К используется соответственно 177 и 45 фиксированных несущих. Номера выделенных для этих целей несущих заданы в виде таблицы [3], в которой первый и последний номер совпадает со значениями Кmin и Кmax (рис. 7). Фиксированные несущие модулируются опорной псевдослучайной последовательностью.
Всего для этой цели в режимах 8К и 2К используется соответственно 177 и 45 фиксированных несущих. Номера выделенных для этих целей несущих заданы в виде таблицы [3], в которой первый и последний номер совпадает со значениями Кmin и Кmax (рис. 7). Фиксированные несущие модулируются опорной псевдослучайной последовательностью.
 информационных потоков, поступают на отдельные передатчики и излучаются в эфир.
информационных потоков, поступают на отдельные передатчики и излучаются в эфир. (1),
(1), – в общем случае это
– в общем случае это  x
x  матрица (для случая с
матрица (для случая с  приемными и
приемными и  передающими антеннами – квадратная матрица), элементами которой являются комплексные числа
передающими антеннами – квадратная матрица), элементами которой являются комплексные числа 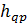 , отображающие коэффициенты передачи трасс от p-ой передающей антенны к q-ой приемной,
, отображающие коэффициенты передачи трасс от p-ой передающей антенны к q-ой приемной,  – вектор столбец, отображающий сообщения, передаваемые в эфир одновременно со всех передающих антенн (размерность
– вектор столбец, отображающий сообщения, передаваемые в эфир одновременно со всех передающих антенн (размерность  ),
),  – вектор столбец шумов (размерность
– вектор столбец шумов (размерность  ), приведенных ко входам приемников (в групповом приемнике с демодулятором), подключенных к выходам приемных антенн, и, наконец,
), приведенных ко входам приемников (в групповом приемнике с демодулятором), подключенных к выходам приемных антенн, и, наконец,  – вектор наблюдений (размерность
– вектор наблюдений (размерность 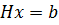 (H – линейный оператор, x – искомый вектор, b – вектор наблюдений) к дополнительным случайным воздействиям. Соответственно, если число обусловленности близко к единице, то матрицу такой системы называют хорошо обусловленной. При этом, чем больше число обусловленности Н, тем, как правило, больше будет погрешность в получаемого решения и, применительно к интересующему нас случаю, выше вероятность ошибок при передаче информации. Найти число обусловленности по второй норме можно следующим образом:
(H – линейный оператор, x – искомый вектор, b – вектор наблюдений) к дополнительным случайным воздействиям. Соответственно, если число обусловленности близко к единице, то матрицу такой системы называют хорошо обусловленной. При этом, чем больше число обусловленности Н, тем, как правило, больше будет погрешность в получаемого решения и, применительно к интересующему нас случаю, выше вероятность ошибок при передаче информации. Найти число обусловленности по второй норме можно следующим образом: (2),
(2), и
и  – это максимальное и минимальное сингулярные числа матрицы H. В системе Matlab существует специальная встроенная функция для вычисления чисел обусловленности матриц cond [4].
– это максимальное и минимальное сингулярные числа матрицы H. В системе Matlab существует специальная встроенная функция для вычисления чисел обусловленности матриц cond [4].
 (3),
(3),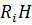 – перебор всех возможных переданных комбинации
– перебор всех возможных переданных комбинации  с учетом оцененного влияния канала
с учетом оцененного влияния канала  ,
,  – принятая комбинация сигналов. Далее биты, полученные путем соответствующей демодуляции принятых сигналов
– принятая комбинация сигналов. Далее биты, полученные путем соответствующей демодуляции принятых сигналов  , поступают на мультиплексор, где выстраиваются в порядке, соответствующем переданному потоку.
, поступают на мультиплексор, где выстраиваются в порядке, соответствующем переданному потоку. (2)
(2) (3)
(3) – принятые символы в первый и второй временной слот, соответственно;
– принятые символы в первый и второй временной слот, соответственно; – коэффициент передачи канала с первой передающей антенны (считаем его постоянным на двух временных интервалах);
– коэффициент передачи канала с первой передающей антенны (считаем его постоянным на двух временных интервалах); – коэффициент передачи канала со второй передающей антенны (считаем его постоянным на двух временных интервалах);
– коэффициент передачи канала со второй передающей антенны (считаем его постоянным на двух временных интервалах); – переданные символы;
– переданные символы; – отсчеты шума в первом и втором слоте, соответственно.
– отсчеты шума в первом и втором слоте, соответственно. и
и  из принятых
из принятых 


