
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Усовершенствованный метод Эйлера.Содержание книги
Поиск на нашем сайте Существуют различные модификации метода Эйлера, повышающие его точность. Они обычно направлены на то, чтобы более точно определить переход от точки
При использовании этого метода сначала по формуле Эйлера найдем приближенное решение в середине интервала, т.е.
Затем в середине отрезка, т.е. точке ( Следовательно, формулу (1) можно записать следующим образом
С помощью метода Эйлера-Коши можно проводить контроль точности решения путем сравнения промежуточного значения функции в i+1 узле с ее окончательным значением в этом узле, т.е. значений Метод Рунге-Кутта. Широкая категория методов, наиболее часто применяемых на практике для решения дифференциальных уравнений, известна под общим названием: методы Рунге - Кутта. Различные методы этой категории требуют большего или меньшего объема вычислений и, соответственно, обеспечивают большую или меньшую точность. Методы Рунге - Кутта обладают следующими отличительными свойствами: эти методы являются одноступенчатыми: чтобы найти значение функции в точке yi +1 нужна информация только о предыдущей точке (yi, xi); они согласуются с рядом Тейлора вплоть до членов порядка hk, где степень k определяет порядок метода; эти методы не требуют вычисления производных от f (x, y), а требуют вычисления самой функции. Именно благодаря последнему свойству методы Рунге - Кутта более удобны для практических вычислений. 32. Решение транспортной задачи методом потенциалов. 30. Транспортная задача.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 в точку
в точку  .Усовершенствованным методом Эйлера называется метод, который использует формулу следующего вида
.Усовершенствованным методом Эйлера называется метод, который использует формулу следующего вида (1)
(1) (2)
(2) ,
,  ) вычисляем значение функции
) вычисляем значение функции 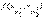 , т.е. определяем в этой точке наклон интегральной кривой
, т.е. определяем в этой точке наклон интегральной кривой  . Используя эти найденные промежуточные значения вычисляем значение сеточной функции по формуле (1).
. Используя эти найденные промежуточные значения вычисляем значение сеточной функции по формуле (1).
 и
и  . На основании этого сравнения выбирается величина шага h в каждом узле. Если модуль разности этих значений сравним с погрешностью вычислений, т.е. выполняется неравенство
. На основании этого сравнения выбирается величина шага h в каждом узле. Если модуль разности этих значений сравним с погрешностью вычислений, т.е. выполняется неравенство  , то шаг можно увеличить.
, то шаг можно увеличить.


