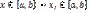Квадратурные формулы Гаусса.

Рассмотрим способ представления квадратных формул состоящих в пред-ии интеграла как линейной комбинации значения под интегральной функции и ее производных в некоторых узлах x_i по следующим определениям неизвестных коэффициентов. Строим квадратурную формулу следующего вида: I = ^bò_a f(x) dx» (a-b) [A₁f(a) + A₂f(b) + A₃f’(a)

+ A₄f’(b)] Ai(i= 1,2,3,4) весовым множества.

Определим весовые множества так, что бы формула была точной для производных многочленов нулевой первой второй и третьей степеней. Это условие будет выполняться, если оно выполняется для многочленов: 1, x², x², x³. подставляем эти многочлены вместо f(x) в формулу получим систему линейных уравнений относительно A_i. Решив систему находим A₁=A₂=1/2; A₃=A₄=(b-a)/12. Квадратурная формула Гаусса:

I = ^bò_a f(x) dx»(a-b) [(f(a)+f(b))/2 + (b-a)* (f’’(a)-f’’(b))/12]

Метод Пикара решения Д.У.

Позволяет получить приближённое знач. ДУ y’=f(x,y) в виде ф-и, представленной аналитически. Пусть в условиях теоремы существования требуется найти решение уравнения y’=f(x,y) с начальным условием y(x0)=y0. Проинтегрируем обе части уравнения y’=f(x,y) от х0 до х или

Решение ИУ будет удовлетворять ДУ и начальному условию. При х=х0 получим:

ИУ позволяет позволяет применить метод последовательных приближений. Будем рассматривать правую часть ф-лы как оператор, отображаущий всякую ф-ю в другую ф-ю того же класса

Если этот опратор является сжимающим, то можно строить последовательность приближений, сходящуюся к точному решению. В качестве начального приближения принимается y=(x)=y0, и находится первое приближение

Интеграл в правой части содержит только переменную х, после нахождения этого интеграла будет получено аналитическое выражение приближения y1(x) как ф-и переменной х. Далее заменим в правой части ур. у найденным значением y1(x) и получим второе приблидение

и т.д. В общем случае итерационная формула имеет вид

Циклическое применение формулы даёт последовательность ф-й y0 y1 yn сходящуюся к решению интегрального уравнения (6.7) (а, следовательно, и дифференциального уравнения (6.1) с начальными условиями (6.2)). Это также означает, что к-й член последовательности (6.9) является приближением к точному решению уравнения (6.1) с определенной контролируемой степенью точности. Оценка погрешности k-го приближения дается формулой

где y(x)- точное решение N определяется равенстовом, M-константа Липшица из неравентсва

Метод Эйлера решения Д.У.

1)Универсальный численный метод решения д.у. – метод конечных разностей. Сущность – замена области непрерывного измерения аргумента дискретным множеством точек (сеткой или сеточной области с постоянным или переменным шагом h).

Аппроксимация д.у.

2) Решить дифференциальное уравнение у/=f(x,y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0.

Таким образом, численные методы позволяют вместо нахождения функции

У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка

y/=f(x,y) (1)

с начальным условием

x=x0, y(x0)=y0 (2)