
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи теорії масового обслуговування. Основні поняття.⇐ ПредыдущаяСтр 21 из 21
Класифікація СМО При дослідженні складних систем доводиться зіштовхуватися із системами, призначеними для багаторазового використання при розв'язанні однотипних задач. Виникаючі при цьому процеси отримали назву процесів обслуговування, а системи - систем масового обслуговування (СМО). Прикладами таких систем є телефонні системи, ремонтні майстерні, обчислювальні комплекси, квиткові каси, магазини, перукарні і т. інше. Кожна СМО складається з певного числа обслуговуючих одиниць (приладів, пристроїв, пунктів, станцій), які будемо називати каналами обслуговування. Каналами можуть бути лінії зв'язку, робочі точки, обчислювальні машини, продавці і т. інше. По числу каналів СМО підрозділяють на одноканальні й многоканальні. Заявки надходять до СМО звичайно не регулярно, а випадково, утворюють так званий випадковий потік заявок (вимог). Обслуговування заявок також триває якийсь випадковий час. Випадковий характер потоку заявок і часу обслуговування приводить до того, що СМО виявляється завантаженою нерівномірно: в якісь періоди часу накопичується дуже велика кількість заявок (вони або стають у чергу, або залишають СМО не обслугованими), в інші ж періоди СМО працює з недовантаженням або простоює. Предметом теорії масового обслуговування є побудова математичних моделей, що зв'язують задані умови роботи СМО (число каналів, їхня продуктивність, характер потік заявок і т.п.) з показниками ефективності СМО, що описують її спроможність справлятися з потоком заявок. Як показники ефективності СМО використовуються: середнє число заявок, що обслуговуються в одиницю часу; середнє число заявок у черзі; середній час сподівання обслуговування; імовірність відмови в обслуговуванні без сподівання; імовірність того, що число заявок у черзі перевищить певне значення і т. інше. СМО ділять на два основних класи: СМО з відмовами й СМО з сподіванням (із чергою). У СМО з відмовами заявка, що надійшла в момент, коли всі канали зайняті, одержує відмову, залишає СМО й надалі процесі обслуговування не бере участь (наприклад, заявка на телефонну розмову в момент, коли всі канали зайняті, одержує відмову й залишає СМО не обслугованою). У СМО з сподіванням заявка, що прийшла в момент, коли всі канали зайняті, не іде, а стає в чергу на обслуговування.
СМО з сподіванням підрозділяються на різні види залежно від того, як організована черга: з обмеженою або необмеженою довжиною черги, з обмеженим часом сподівання і т. інше. Для класифікації СМО важливе значення має дисципліна обслуговування, яка визначає порядок вибору заявок із числа що надійшли і порядок розподілу їх між вільними каналами. За цією ознакою обслуговування заявки може бути організоване за принципом "перша прийшла - перша обслугована", "остання прийшла - перша обслугована".
Поняття марковського випадкового процесу Процес роботи СМО являє собою випадковий процес. Під випадковим процесом розуміється процес зміни в часі стану якої-небудь системи відповідно до імовірнісних закономірностей. Процес називається процесом з дискретними станами, якщо його можливі стани S1, S2,... можна заздалегідь перелічити, а перехід системи зі стану в стан відбувається миттєво (стрибком). Процес називається процесом з безперервним часом, якщо моменти можливих переходів системи зі стану в стан не фіксовані заздалегідь, а випадкові. Процес роботи СМО являє собою випадковий процес із дискретними станами й безперервним часом. Це означає, що стан СМО змінюється стрибком у випадкові моменти появи якихось подій (наприклад, приходу нової заявки, закінчення обслуговування і т. інше.). Математичний аналіз роботи СМО істотно спрощується, якщо процес цієї роботи - марковський. Випадковий процес називається марковським або випадковим процесом без післядії, якщо для будь-якого моменту часу t0 імовірнісні характеристики процесу в майбутньому залежать тільки від його стану в цей момент t0 і не залежать від того, коли і як система прийшла в цей стан. Приклад марковського процесу: система S - лічильник у таксі. Стан системи в момент t характеризується числом кілометрів, що пройшов автомобіль на даний момент. Нехай у момент t0 лічильник показує S0. Імовірність того, що в момент t > t0 лічильник покаже те чи інше число кілометрів S1, залежить від S0, але не залежить від того, в які моменти часу змінювалися дані лічильника до моменту t0.
Багато процесів можна приблизно вважати марковськими, тому що в ряді випадків передісторією розглянутих процесів можна просто зневажити й застосовувати для їхнього вивчення марковські моделі. Для математичного опису марковського випадкового процесу з дискретними станами й безперервним часом, що протікає в СМО, познайомимося з одним з важливих понять - поняттям потоку подій.
Потоки подій Під потоком подій розуміється послідовність однорідних подій, що випливають одне за іншим у якісь випадкові моменти часу (наприклад, потік викликів на телефонній станції, потік відмов ЕОМ, потік покупців і т. інше.). Потік характеризується інтенсивністю l - частотою появи подій або середнім числом подій, що надходять у СМО за одиницю часу. Потік подій називається стаціонарним, якщо його імовірнісні характеристики не залежать від часу. Зокрема, інтенсивність стаціонарного потоку є величина постійна: l(t)=l. Потік подій називається потоком без післядії, якщо для будь-яких двох непересічних ділянок часу t1 і t2 - число подій, що попадають на один з них, не залежить від числа подій, що попадають на інші. Потік подій називається ординарним, якщо ймовірність падання на малий (елементарний) відрізок часу Dt двох і більше подій мала в порівнянні з імовірністю влучення однієї події. Нагадаємо, що потік подій називається найпростішим, якщо він одночасно стаціонарний, ординарний, і не має післядії. Назва "найпростіший" пояснює тим, що СМО з найпростішими потоками має найбільш простий математичний опис. Для найпростішого потоку число m подій, що попадають на довільну дільницю часу t, розподілене за законом Пуассона Рm(t)= для якого математичне сподівання випадкової величини дорівнює її дисперсії: а = s2 = lt. Зокрема, імовірність того, що за час t не відбудеться жодної події (m=0), дорівнює: Р0 = е-lt. Інтервал часу між довільними двома сусідніми подіями найпростішого потоку Т розподілений за експонентним законом: F(t) = Р(Т < t) = 1 – е-lt. Щільність імовірності випадкової величини Т є похідна її функції розподілу, тобто: f(t)=F'(t)= lе-lt. Математичне сподівання дорівнює середньому квадратичному відхиленню випадкової величини: а = s = і зворотне за величиною інтенсивності потоку. Найважливіша властивість показового розподілу (присутня тільки показовому розподілу) полягає в наступному: якщо проміжок часу, розподілений за показовим законом, уже тривав якийсь час t, то це ніяк не впливає на закон розподілу частини, що залишилася, проміжку (Т-t): він буде таким же, як і закон розподілу всього проміжку Т. Інакше кажучи, для інтервалу часу Т між двома послідовними сусідніми подіями потоку, що має показовий розподіл, будь-які відомості про те, скільки часу протікав цей інтервал, не впливають на закон розподілу частини, що залишилася. Це властивість показового закону являє собою, по суті, інше формулювання для "відсутності післядії" - основної властивості найпростішого потоку.
СМО з відмовами. Сталий режим обслуговування Розглянемо функціонування системи з відмовами. Нехай є n-канальна система, яку можна представити як фізичну систему з кінцевою множиною станів: S0 – всі канали вільні, S1 – зайнятий рівно один канал, Sk – зайнято рівно k каналів,…, Sn–зайняті всі n каналів. Схема можливих станів системи показана на рис 12.7:
Імовірності станів системи pk(t) для будь-якого моменту часу t можна визначити в такий спосіб. Нехай потоки заявок на обслуговування й визволення є найпростішими, і інтервал між заявками розподілений за експонентним законом з параметром l: f(t) = le-lt. а час перебування заявки на обслуговуванні також розподілено за експонентним законом з параметром m: g(t) = me-mt. Тоді процес зміни станів системи буде марковським, що дозволяє скласти лінійні диференціальні рівняння відносно ймовірностей станів системи. Складемо рівняння для pk(t) (1£k£n). Зафіксуємо момент часу t і знайдемо ймовірність pk(t+Dt) того, що в момент часу t+Dt система буде в стані Sk. Ця ймовірність обчислюється як імовірність суми трьох подій А, В і С (за числом стрілок, що спрямовані у стан Sk на рис. 12.7): подія А={в момент t система перебувала в стані Sk і за час Dt заявка не надійшла й жоден канал не звільнився}; подія В={у момент t система перебувала в стані Sk-1, і за час Dt надійшла одна заявка}; подія С={у момент t система перебувала в стані Sk+1, і за час Dt канал звільнився}. За теоремою додавання ймовірностей маємо: pk(t+(t) = Р(А) + Р(В) + Р(З). (12.13) Імовірність події А, тобто того, що за час Dt не надійшла жодна заявка й жоден канал не звільнився, знайдемо відповідно до теореми множення ймовірностей:
Нехтуючи величинами малих порядків, маємо:
тоді
Аналогічно визначимо ймовірності подій В і С:
Підставивши (12.14), (12.15) і (12.16) в (12.13), дістанемо
Перенесемо pk(t) у ліву частину рівняння, розділивши на Dt і перейшовши до границі при Dt®0, дістанемо диференціальне рівняння для pk(t):
Аналогічним способом можна дістати диференціальні рівняння для ймовірностей станів системи при k=0 і k=n:
Система рівнянь (12.17) називається рівняннями Колмогорова. Інтегрування цієї системи за початкових умов р0(0) =1, р1(0) =…=рn(0) =0 (у початковий момент часу всі канали вільні) дозволяє знайти ймовірність кожного з Імовірність q(t)=1-pk(t) називається відносною пропускною спроможністю системи. Для даного t це є відношення середнього числа обслугованих за одиницю часу заявок до середнього числа поданих. Рівняння Колмогорова дають можливість знайти всі ймовірності станів як функції часу. Особливий інтерес представляють імовірності системи рk(t) у граничному стаціонарному режимі, тобто при t®¥, які називаються граничними (або фінальними) ймовірностями станів.
Теорія випадкових процесів доводить, що якщо число станів системи скінченне й з кожного з них можна (за кінцеве число кроків) перейти в будь-який інший стан, то граничні ймовірності існують. Гранична ймовірність стану Sk, має чіткий сенс: вона показує середній відносний час перебування системи в цьому стані. Наприклад, якщо гранична ймовірність стану S0, тобто р0=0,5, то це означає, що в середньому половину часу система перебуває в стані S0. Оскільки граничні ймовірності постійні, то, заміняючи в рівняннях Колмогорова їхні похідні нульовими значеннями, дістанемо систему лінійних алгебраїчних рівнянь, що описують стаціонарний режим:
Розв’язавши систему (12.20) щодо ймовірностей, отримаємо для будь-якого k:
Позначимо l/m=a і назвемо її приведеною інтенсивністю потоку заявок, що є ні що інше, як число заявок, що доводиться на середній час обслуговування однієї заявки. При цьому формула (12.21) матиме вигляд:
Звідки, урахувавши, що
Виразимо звідси р0, підставимо в формулу (12.22) та отримаємо:
Формула (12.23) називається формулою Эрланга. Вона дає граничний закон розподілу числа зайнятих каналів залежно від характеристик потоку заявок і продуктивності системи обслуговування. Помітимо, що незважаючи на те, що формули Эрланга в точності справедливі тільки для найпростішого потоку заявок, ними з відомим наближенням можна користуватися й для потоків з обмеженою післядією, а також для систем з очікуванням, коли строк очікування заявки в черзі малий у порівнянні із середнім часом обслуговування.
СМО з очікуванням. Метод статистичних випробувань Якщо заявка, що застала всі канали зайнятими, стає в чергу й чекає, поки звільниться який-небудь канал, причому час сподівання не обмежений, то така система називається чистою системою з очікуванням. Якщо час очікування обмежений, то система називається системою змішаного типу. Обмеження можуть накладатися на час очікування заявки в черзі, на число заявок у черзі. При цьому заявки, що очікують, можуть викликатися на обслуговування за чергою, у випадковому або пільговому порядку. Кожний тип системи має свої особливості й свою методику розрахунку. Наприклад, змішані системи деяких типів можуть бути описані диференціальними рівняннями, аналогічними рівнянням Эрланга. При цьому час очікування заявки в черзі, як і час її обслуговування, вважається випадковим, розподіленим за експонентним законом. Це дозволяє вважати процеси, що протікають у системі, марковськими. У тих випадках, коли випадкові процеси не можна віднести до класу марковських, аналітичне вираження для розрахунку ймовірностей станів системи одержати не вдається. У цьому випадку користуються універсальним методом статистичних випробувань або, як його часто називають, методом Монте-Карло.
У першому наближенні ідею методу можна описати так: процес функціонування складної системи імітується на ЕОМ з усіма супровідними його випадками. Таким чином, будується одна реалізація випадкового процесу з випадковим ходом і результатом. Сама по собі така реалізація не дає підстав до вибору рішення, але, одержавши множину таких реалізацій, можна їх обробити як звичайний статистичний матеріал, визначити середні характеристики по множині й одержати подання про те, які умови задачі й елементи рішення впливають на функціонування системи. Таким чином, при використанні методу Монте-Карло випадковість використовується як апарат дослідження. Для систем, у яких бере участь велика кількість різнорідних елементів, а випадкові фактори складним способом взаємодіють між собою, процеси неможливо описати аналітично як за допомогою детермінованих, так і ймовірнісних методів, а імітаційне моделювання, як правило, виявляється простіше аналітичного, а нерідко і єдино можливим методом моделювання. СПИСОК ЛІТЕРАТУРИ 1. Гмурман В. Э. Теория вероятностей и математическая статистика. -М.: Высш. школа, 1977. - 498 с. 2. Гмурман В.Э. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высш. школа, 1975. - 330с. 3. Вентцель Е. С. Теория вероятностей. - М.: Высшая школа, 1999. 4. Гнеденко Б.В. Курс теории вероятностей.- Физматгиз, 1961. 5. Вентцель Е. С., Овчаров Л.А. Сборник задач по теории вероятностей. - М.: Наука, 1969. 6. Сборник задач по теории вероятностей, математической статистике и теории случайных функций./ Под ред. А.А.Свешникова.- Наука, 1970.
ЗМІСТ
ВСТУП............................................................................................. 3 ЗМ 1. ІМОВІРНІСТЬ ВИПАДКОВОЇ ПОДІЇ.................................. 7 Тема1. Основні поняття теорії ймовірностей.................................. 7 Класичний і статистичний методи визначення ймовірності випадкової події............................................................................... 8 Тема 2. Операції над подіями. Теореми теорії ймовірностей Основні формули теорії ймовірностей............................................ 10 Теорема додавання........................................................................... 11 Теорема множення........................................................................... 13 Формула повної ймовірності........................................................... 14 Формула Бейеса (теорема гіпотез)................................................... 14 Формула Бернуллі........................................................................... 15 Локальна теорема Лапласа.............................................................. 16 Інтегральна теорема Лапласа.......................................................... 16 Формула Пуассона........................................................................... 17 ЗМ 2. ВИПАДКОВІ ВЕЛИЧИНИ І ЇХНІ ЗАКОНИ РОЗПОДІЛУ. 18 Тема 3. Поняття випадкової величини і закону розподілу. Універсальні закони розподілу....................................................... 18 Функція розподілу........................................................................... 19 Щільність розподілу........................................................................ 20 Тема 4. Числові характеристики випадкової величини.................. 22 Властивості числових характеристик.............................................. 25 Тема 5. Найбільш важливі для практики закони розподілу випадкових величин......................................................................... 26 Біноміальний закон розподілу......................................................... 26 Закон розподілу Пуассона............................................................... 28 Експонентний закон розподілу........................................................ 29 Нормальний закон розподілу ймовірностей................................... 31 Поняття про центральну граничну теорему................................... 34 Закон рівномірної щільності............................................................ 35 Тема 6. Система випадкових величин. Закони розподілу й числові характеристики системи................................................... 37 Багатомірна випадкова величина.................................................... 37 Функція розподілу системи двох випадкових величин.................. 37 Щільність розподілу системи двох випадкових величин............... 38 Числові характеристики системи випадкових величин................... 38 Функції випадкових величин........................................................... 40 Тема 7. Закон великих чисел............................................................ 43 Принцип практичної впевненості. Формулювання закону великих чисел................................................................................... 43 ЗМ 3. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ............... 49 Тема 8. Основні поняття. Суть вибіркового методу....................... 49 Визначення закону розподілу спостережуваної ознаки за статистичними даними..................................................... 54 Тема 9. Числові характеристики варіаційного ряду....................... 56 Властивості вибіркових числових характеристик.......................... 58 Довірчий інтервал і довірча імовірність......................................... 60 Тема 10. Елементи теорії кореляції................................................. 62 Метод найменших квадратів............................................................ 64 Вибірковий коефіцієнт кореляції..................................................... 66 Вибіркове кореляційне відношення................................................. 68 Елементи регресійного аналізу........................................................ 69 Тема 11. Перевірка статистичних гіпотез........................................ 71 Статистичні гіпотези......................................................................... 71 Порівняння вибіркової середньої й генеральної середньої нормальної сукупності..................................................................... 74 Порівняння двох дисперсій нормальних генеральних сукупностей 76 Критерії згоди.................................................................................. 77 Елементи дисперсійного аналізу..................................................... 79 Тема 12. Елементи теорії випадкових процесів.............................. 82 Поняття випадкового процесу......................................................... 82 Стаціонарний випадковий процес................................................... 85 Ергодична гіпотеза........................................................................... 88 Елементи теорії масового обслуговування. Основні поняття. Класифікація СМО........................................................................... 90 Поняття марковського випадкового процесу................................. 92 Потоки подій..................................................................................... 93 СМО з відмовами. Сталий режим обслуговування........................ 94 СМО з очікуванням. Метод статистичних випробувань................98 СПИСОК ЛІТЕРАТУРИ................................................................100
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.196.59 (0.082 с.) |
 ,
,

 .
. ,
, . (12.14)
. (12.14)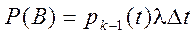 , (12.15)
, (12.15) . (12.16)
. (12.16) .
. (12.17)
(12.17) , (12.18)
, (12.18) . (12.19)
. (12.19) станів системи. Імовірність рn(t) – це імовірність того, що заявка, що прийшла в момент часу t, застане всі канали зайнятими, тобто одержить відмову.
станів системи. Імовірність рn(t) – це імовірність того, що заявка, що прийшла в момент часу t, застане всі канали зайнятими, тобто одержить відмову. . (12.20)
. (12.20) . (12.21)
. (12.21) . (12.22)
. (12.22) , одержимо:
, одержимо: .
. , де
, де 


