
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Бейеса (теорема гіпотез)
Ця формула дозволяє за відомими до проведення досліду (апріорним) ймовірностями гіпотез Р(Нi) і за результатом досліду (наступ події А) визначити обчислені після досліду (апостеріорні) імовірності гіпотез Р(Нi|А). За теоремою множення імовірність появи події А при i-й гіпотезі Р(Нi*А)= Р(Нi)*Р(А|Нi) у чинність симетрії подій справедливо Р(Нi*А)= Р(А)*Р(Нi|А), звідки дістанемо
або, якщо підставити Р(А) з формули (2.6), дістанемо
Таким чином, формула Бейеса дозволяє переоцінити імовірності гіпотез після того, як стає відомим результат досліду, в результаті якого відбулася подія А. Формула Бернуллі На практиці доводиться зіштовхуватися з такими задачами, які можна представити у вигляді багаторазово повторюваних незалежних випробувань. Якщо імовірність появи події А в одному досліді та сама, то імовірність m появ події А в n дослідах можна визначити за формулою Бернуллі
де
р - імовірність появи події А в одному досліді; q = 1 - p - імовірність не появи події А в одному досліді. Користуючись формулою Бернуллі, можна дістати найімовірніше число появ події А. Найімовірнішим числом появи події А в n незалежних дослідах називається таке число, для якого імовірність перевищує або, принаймні, не менше ймовірності кожного з інших можливих чисел появи події А. Для визначення найімовірнішого числа користуються формулою: np – q £ m0 £ np + p (2.9) причому, m0 — може бути тільки цілим числом. Якщо np - ціле число, то m0=np. Локальна теорема Лапласа Локальна теорема Лапласа дає асимптотичну формулу, що дозволяє приблизно знайти імовірність появи подій рівно m разів в n дослідах, якщо число випробувань досить велике. Якщо імовірність р появи події А в кожному випробуванні постійна й відмінна від нуля й одиниці, то імовірність Pn(m) того, що подія А з'явиться в n дослідах рівно m разів, приблизно дорівнює, і тим точніше, чим більше n, значенню функції
де
Інтегральна теорема Лапласа Якщо в повторних незалежних випробуваннях, у кожному з яких імовірність появи події А постійна й дорівнює р, необхідно обчислити ймовірність того, що подія А з'явиться в n випробуваннях не менше m1 і не більше m2 разів, це можна зробити за допомогою інтегральної теореми Лапласа.
Якщо імовірність р настання події А в кожному випробуванні постійна й відмінна від нуля й одиниці, то приблизно імовірність Pn(m1,m2), того, що подія А з'явиться у випробуваннях від m1 до m2 разів,
де При розв'язанні задач користуються спеціальними таблицями, тому що невизначений інтеграл (2.11) не виражається через елементарні функції. У довідкових таблицях приводяться значення інтеграла Таким чином, приблизно імовірність того, що подія А з'явиться в n незалежних дослідах від m1 до m2 разів. Pn(m1,m2) = Ф(х")-Ф(х'), (2.12)
Формула Пуассона Якщо імовірність р настання події в окремому випробуванні близька до нуля, то навіть при великій кількості випробувань n, але при невеликому значенні добутку np одержувані за формулою Лапласа значення ймовірностей Рn(m) виявляються недостатньо точними й виникає потреба в іншій наближеній формулі. Якщо імовірність р настання події А в кожному випробуванні постійна, але мала, число незалежних випробувань n досить велике, але значення добутку np залишається невеликим (не більше десяти), то імовірність того, що в цих випробуваннях подія А наступить m разів, можна визначити за формулою Пуассона:
Змістовий модуль 2
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.5.239 (0.027 с.) |
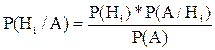 ,
, (2.7)
(2.7) (2.8)
(2.8) - імовірність того, що в n випробуваннях подія А з'явиться рівно m разів;
- імовірність того, що в n випробуваннях подія А з'явиться рівно m разів; - число сполучень із n елементів по m;
- число сполучень із n елементів по m; , (2.10)
, (2.10) , а значення функції
, а значення функції  визначаються з довідкових таблиць. Функція j (х) парна, тобто j (-х) = j (х).
визначаються з довідкових таблиць. Функція j (х) парна, тобто j (-х) = j (х). , (2.11)
, (2.11) ;
; 
 . Функція Ф(х) непарна, тобто Ф(-х) = -Ф(х). Таблиця містить значення функції Ф(х) тільки для х Î [0; 5]; для х > 5 приймають Ф(х) = 0,5.
. Функція Ф(х) непарна, тобто Ф(-х) = -Ф(х). Таблиця містить значення функції Ф(х) тільки для х Î [0; 5]; для х > 5 приймають Ф(х) = 0,5. (2.13)
(2.13)


