
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Числові характеристики випадкової величиниСодержание книги
Поиск на нашем сайте
Закон розподілу випадкової величини являє собою деяку функцію, що цілком описує випадкову величину з імовірнісної точки зору, тобто є її вичерпною характеристикою й дозволяє визначати імовірності будь-яких подій, пов'язаних з випадковою величиною. Однак у багатьох практичних задачах потрібно отримати більш компактне уявлення про випадкову величину. Для теорії ймовірностей і її застосування велику роль грають деякі постійні числа, що одержані за певними правилами із законів розподілу випадкових величин і названі числовими характеристиками випадкової величини. Найважливішою числовою характеристикою випадкової величини є математичне сподівання. Математичним сподіванням випадкової величини Х називається сума добутків всіх можливих її значень на імовірності цих значень
Математичне сподівання характеризує середнє значення випадкової величини, навколо якого групуються всі її можливі значення. На практиці використовується ряд числових характеристик, які характеризують особливості розподілу випадкової величини. Такими характеристиками є так звані моменти або математичні сподівання випадкової величини. Розрізняють початкові a і центральні m моменти. Початковим моментом s -го порядку дискретної випадкової величини називається математичне сподівання s-го ступеня цієї величини
Для безперервної випадкової величини початковий момент s -го порядку
Вираження (4.2) і (4.3) можна об'єднати в одне, користуючись знаком математичного сподівання M:
тобто початковим моментом s -го порядку випадкової величини називається математичне сподівання s -го ступеня цієї випадкової величини. При s = 1 дістаємо перший початковий момент або математичне сподівання випадкової величини
На практиці іноді застосовують другий початковий момент a2:
Центральним моментом s-го порядку випадкової величини X називається математичне сподівання s -го ступеня центрованої величини X. Під центрованою розуміється відхилення випадкової величини від її математичного сподівання:
Центральний момент s-го порядку випадкової величини Х виражається формулою
Для дискретної випадкової величини Х:
Для безперервної випадкової величини Х:
Центральний момент першого порядку дорівнює нулю:
Центральний момент другого порядку для дискретної випадкової величини Х:
Для безперервної випадкової величини:
Другий центральний момент називається дисперсією. Дисперсія випадкової величини є характеристикою розсіювання цієї величини навколо математичного сподівання. У випадку, якщо це розсіювання відсутнє, величина Dx дорівнює нулю. Дисперсія має розмірність квадрата випадкової величини, що не завжди зручно. Тому як характеристику розсіювання часто використовують середнє квадратичне відхилення Х: sх = ÖDx. (4.12) Центральні моменти більш високого порядку можуть характеризувати ступінь асиметрії розподілу випадкової величини, крутість кривої розподілу і т. інше.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.174 (0.007 с.) |

 . (4.1)
. (4.1) . (4.2)
. (4.2) . (4.3)
. (4.3)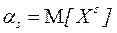 , (4.4)
, (4.4) . (4.5)
. (4.5) (4.6)
(4.6)
 (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9) .
. (4.10)
(4.10) (4.11)
(4.11)


