
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові характеристики системи випадкових величин
Початковим моментом порядку k,s системи двох випадкових величин називається математичне сподівання добутку випадкових величин X, Y у ступені k і s:
Відповідно центральним моментом порядку k,s системи випадкових величин (X, Y) називається математичне сподівання добутку центрованих величин X, Y у ступені k і s:
Для опису системи двох випадкових величин крім математичних сподівань і дисперсій X і Y використовують кореляційний момент і коефіцієнт кореляції. Кореляційним моментом є другий змішаний центральний момент:
Для дискретної випадкової величини Kxy визначається за формулою:
де pij = P{X=xi|Y=yj} – умовна ймовірність, тобто імовірність того, що X прийме значення xi за умови, що Y прийме значення yj. Для безперервної випадкової величини:
Якщо події P{X=xi} і P{Y=yj} незалежні, то імовірність їхньої спільної появи за теоремою добутку дорівнює pij = P{X=xi} * P{Y=yj} = pi * pj. Тоді для кореляційного моменту справедливе вираження:
тому що співмножники є центральними моментами першого порядку випадкових величин Х і Y. Таким чином, кореляційний момент є характеристикою зв'язку між величинами X і Y, і у випадку незалежних X і Y він дорівнює нулю. Як другий змішаний центральний момент кореляційний момент утримує також і розсіювання випадкових величин X і Yвідносно один одного. Тому він не може характеризувати тісноту зв'язку між X і Y.Для визначення тісноти зв'язку між X і Y використовують коефіцієнт кореляції rxy, який визначається за формулою:
Переконаємося в тому, що rxy характеризує ступінь тісноти лінійного зв'язку між двома випадковими величинами. Нехай випадкова величина Y функціонально (жорстко) залежить від випадкової величини Х, причому залежність ця лінійна: Y = a+b Визначимо математичне сподівання M[Y] = M[a+b] = S(axi+b)pi = aSxipi +Sbpi = a[X]+b. Знайдемо дисперсію: D[Y] = M[ =M[(a+b)2-2(amx+b)(a+b)+ (amx+b)2] = M[a2(X-mx)2]=a2Dx, а середнє квадратичне відхилення Y sy = |a|sx. Визначимо коефіцієнт кореляції для жорстко зв'язаних X і Y, для чого виразимо
а коефіцієнт кореляції
Таким чином, якщо зв'язок функціональний, то коефіцієнт кореляції дорівнює 1, причому
У загальному випадку коефіцієнт кореляції лежить у межах -1£rxy£+1 і дорівнює нулю, якщо X і Y незалежні.
Поняття корельованості й залежності двох випадкових величин різні. Дві корельовані випадкові величини обов'язково залежні. Дві залежні випадкові величини необов'язковокорельовані.
Функції випадкових величин Функції однієї або декількох випадкових величин доводиться розглядати, коли аргументом деякої функції Y є система випадкових величин (X1, X2,…, Xn), закон розподілу яких відомий. Функція Y є випадковою величиною, закон розподілу якої варто визначити. У більшості задач для визначення числових характеристик функції декількох випадкових величин досить знати тільки числові характеристики аргументів. 1. Математичне сподівання суми двох залежних або незалежних випадкових величин X і Y дорівнює сумі їхніх математичних сподівань: M[X+Y] = S(xi+yi)pi = Sxipi +Syipi = M[X] + M[Y]. (6.10) Методом математичної індукції (узагальнення) дістанемо: M[SXi] = SM[Xi], Математичне сподівання суми n випадкових величин дорівнює сумі їхніх математичних сподівань. 2. Математичне сподівання добутку двох випадкових величин X і Y дорівнює добутку їхніх математичних сподівань плюс кореляційний момент. Запишемо вираження для кореляційного моменту:
звідки дістанемо M[XY] = M[X] * M[Y] + Kxy.(6.11) Якщо випадкові величини X і Y незалежні, математичне сподівання добутку дорівнює добутку їхніх математичних сподівань. 3. Дисперсія суми двох випадкових величин X і Y дорівнює сумі дисперсій цих величин плюс подвоєний кореляційний момент: D[X+Y] = M[((X+Y)-M(X+Y))2] = =M[X2+2XY+Y2 -2(X+Y)M(X+Y)+M 2(X+Y)] = = M[X2+2XY+Y2]-2M(X+Y)M(X+Y)+M 2(X+Y) = = M[X2+2XY+Y2]-(M[X]+ M[Y])2 = =M[X2]+ M[Y2]-M 2[X]- 2M[X]*M[Y]- M 2[Y] = =D[X] + D[Y]+2M[XY] – 2M[X]M[Y] = D[X] + D[Y]+2Kxy Таким чином, дисперсія суми двох випадкових величин X і Y дорівнює сумі їхніх дисперсій плюс подвоєний кореляційний момент D[X+Y] = D[X] + D[Y] + 2Kxy,(6.12) Якщо X і Y - незалежні випадкові величини, то дисперсія їхньої суми дорівнює сумі їхніх дисперсій, тоді сума n незалежних випадкових величин: D[SXi] = SD[Xi], звідки середнє квадратичне відхилення суми:
4. Дисперсія добутку двох незалежних випадкових величин X і Y визначається за формулою D[XY] = D[X]*D[Y] + M[X]2D[Y] + M[Y]2D[X](6.13)
Тема 7. Закон великих чисел
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.51.241 (0.008 с.) |
 (6.3)
(6.3) (6.4)
(6.4)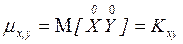 (6.5)
(6.5) , (6.6)
, (6.6) (6.7)
(6.7)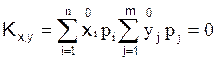 ,
, (6.8)
(6.8) ] = M[(Y-my)2] = M[Y2-2my+my2] =
] = M[(Y-my)2] = M[Y2-2my+my2] = через
через  :
:  , тоді кореляційний момент буде дорівнювати
, тоді кореляційний момент буде дорівнювати
 .
. (6.9)
(6.9)
 ,
, .
.


