
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность модели оценивать по соотношениюСодержание книги
Поиск на нашем сайте
МЕТОДИЧНІ ВКАЗІВКИ до лабораторних робіт з дисциплін "Моделювання систем" для студентів спеціальності 7.080401 – Інформаційні управляючі системи та технології та "Математичне моделювання" для студентів спеціальності 7.091401 – Системи управління та автоматики
Упорядники: В.В. Безкоровайний З.А. Імангулова Н.І. Калита
Відповідальний випусковий Е.Г. Петров
Начальник методичного відділу П.С. Ковтун
Головний редактор УВВПЦ Б.П. Косіковська
поз. ____ Харків 2005 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ
Харьков 2005
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторным работам по дисциплинам "Моделирование систем" для студентов специальности 7.080401 – Информационные управляющие системы и технологии и "Математическое моделирование" для студентов специальности 7.091401 – Системы управления и автоматики
Харьков 2005
Методичні вказівки до лабораторних робіт з дисциплін "Моделювання систем" для студентів спеціальності 7.080401 – Інформаційні управляючі системи та технології та "Математичне моделювання" для студентів спеціальності 7.091401 – Системи управління та автоматики /Упоряд. В.В. Безкоровайний, З.А. Імангулова, Н.І. Калита. – Харків: ХНУРЕ, 2005. – 48 с. – Рос. мовою.
Упорядники: БЕЗКОРОВАЙНИЙ Володимир Валентинович Імангулова Зульфия Аліївна КАЛИТА Надія Іванівна
СОДЕРЖАНИЕ
ОБЩИЕ ПОЛОЖЕНИЯ
Математическое моделирование в настоящее время является обязательной составляющей всех этапов проектирования, создания и эксплуатации технических, организационно-технических и экономических объектов. Использование моделирования позволяет существенно сократить время принятия решений, повысить их качество, спрогнозировать последствия. Наибольшее распространение при этом находит математическое и компьютерное моделирование объектов. Лабораторный практикум ориентирован на активную индивидуальную деятельность каждого студента. Выполнение лабораторных работ направлено на приобретение студентами практических навыков построения моделей и исследования процессов функционирования объектов методами математического моделирования. Каждая работа предусматривает создание, модернизацию или детализацию предложенной модели, проведение экспериментов с машинной моделью, анализ результатов моделирования. Практикум ориентирован на использование студентами современной технологии решения задач моделирования с применением компьютерных средств, пакетов и систем моделирования. Поэтому при подготовке к выполнению работ следует изучить особенности режимов работы и применения используемых программно-технических средств моделирования. С целью сокращения времени на оформление отчета его общие составляющие части рекомендуется выполнять в процессе подготовки к работе. Допуск к выполнению лабораторной работы возможен после проверки подготовленности студентов по контрольным вопросам и заданиям. Чтобы избежать ошибок в процессе выполнения работы следует проводить анализ промежуточных результатов по каждому из ее этапов. По окончании экспериментов необходимо провести детальный анализ полученных результатов, создать электронный или печатный вариант отчета и защитить его во время занятия. Отчет может представляться в электронном или в печатном виде.
Перед выполнением лабораторных работ студенты должны пройти инструктаж по технике безопасности. Ее требований, как и положений инструкций по поведению студентов в лаборатории, а также принятой в университете технологии использования вычислительной техники, необходимо строго придерживаться на протяжении всего лабораторного практикума. Методические указания созданы и оформлены на основе основных требований [1] и рекомендаций [2].
1 ПОСТРОЕНИЕ АНАЛИТИЧЕСКИХ МОДЕЛЕЙ ДИНАМИКИ ОБЪЕКТОВ
1.1 Цель работы
Изучение методики построения аналитических моделей динамики простейшей одномерной системы путем ее идентификации по методу наименьших квадратов. Приобретение навыков выбора вида и параметров модели динамики объекта, экспериментальная оценка точности модели.
1.2 Указания по организации самостоятельной работы При подготовке к выполнению лабораторной работы необходимо: ознакомиться с постановкой задачи построения математических моделей объектов методом идентификации; уяснить суть основных задач, решаемых в процессе идентификации моделей; ознакомиться с классификацией методов идентификации; изучить процедуру идентификации моделей методами наименьших квадратов, а также технологию решения перечисленных задач в среде пакета программ MathCAD. С этой целью может быть использован лекционный материал по соответствующим темам, материал, изложенный в рекомендованной литературе [3, c. 42–50; 4, с. 248–259; 5], а также материал настоящих методических указаний. Практическая часть подготовки к выполнению работы включает создание программы для построения таблиц (графиков), отражающих модельные траектории на одном из языков высокого уровня, или в среде выбранного пакета программ, а также подготовку таблиц для занесения экспериментальных данных. Объектом исследования является одномерная система типа "серый ящик". Задача идентификации формулируется следующим образом: по результатам наблюдения над входными u(t) и выходными y(t) переменными системы необходимо построить оптимальную в смысле минимума квадратов отклонений ее математическую модель. Система находится в свободном движении, т.е. предполагается отсутствие на входе объекта сигналов, т.е. u(t) = t. Выход модели связан с ее входом зависимостью
yм(t) = Fм [uм(t), q, 0], (1.1)
где Fм – оператор модели; uм(t) = t, yм(t) – соответственно входной и выходной сигналы модели; q – вектор параметров модели, q = (q0, q1,..., qm). Сигналы на выходе системы наблюдаются в условиях отсутствия помехи в дискретные моменты времени t1, t2,..., tn и имеют значения y(t1) = y1, y(t2) = y2,..., y(tn) = yn. Выбор модели осуществляется на множестве полиномов Fм = q0 tm + q1 tm-1 +...+ qm, (1.2)
где m – степень полинома модели. В качестве критерия близости использовать минимум суммы квадратов отклонений выходов модели yм(t) от выходов системы y(t)
Наилучшие значения параметров модели являются решениями системы уравнений
или
где n – количество наблюдаемых сигналов (экспериментов). Порядок выполнения работы
Ознакомиться с помощью преподавателя с особенностями и режимами работы используемых компьютерных средств и пакетов программ.
Получить у преподавателя вариант задания (табл. 1.1) и дополнительные исходные данные. Выполнить предварительный анализ данных эксперимента и выбрать вид модели Fм (начальное значение степени полинома (1.2)). Составить систему уравнений вида (1.5) для определения наилучших значений параметров модели q. Определить с помощью выбранного пакета программ наилучшие по критерию (1.3) значения параметров модели qо, построить модельную траекторию движения объекта и оценить точность модели При необходимости ( Найти решение по методу экспоненциального сглаживания (1.7). Сравнить результаты решений по методу наименьших квадратов и методу экспоненциального сглаживания. Сделать выводы, оформить и сдать отчет о выполненной работе. В выводах необходимо указать на наилучшую из рассмотренных моделей, дать оценку ее точности и проанализировать характер изменения точности приближения от степени полинома модели. Провести сравнительный анализ результатов, полученных по методу наименьших квадратов и методу экспоненциального сглаживания. Результатами экспериментов являются значения параметров модели q и выходных координат объекта y(t) и моделей yм(t) для заданного интервала времени.
Таблица 1.1 – Варианты типовых заданий
Содержание отчета
Отчет должен содержать: – цель работы; – постановку и исходные данные задачи; – математические соотношения для вычисления и вычисленные значения параметров модели q; – таблицы со значениями выходных сигналов объекта y(t) и полученных моделей yм(t); – совмещенные графики зависимостей выходных сигналов от времени для объекта y(t) и полученных моделей yм(t); – анализ полученных результатов и выводы по работе.
1.6 Контрольные вопросы и задания 1. Сформулируйте постановку задачи идентификации объекта. 2. Назовите основные задачи, решаемые в процессе идентификации. 3. Нарисуйте и опишите структурную схему процесса идентификации модели. 4. Назовите основные виды критериев идентификации. 5. Приведите классификацию методов идентификации. 6. Запишите критерии для идентификации моделей систем по методам наименьших и наименьших взвешенных квадратов. 7. Запишите систему уравнений для вычисления наилучших значений параметров q модели в виде многочлена. 8. Как определяется степень полинома модели? 9. Запишите систему уравнений для вычисления наилучших значений параметров q модели в виде Fм = q0 exp (q1 t). 10. Запишите систему уравнений для вычисления наилучших значений параметров q модели в виде Fм = q0 tq1. Цель работы
Изучение методов исследования устойчивости математических моделей. Приобретение навыков анализа устойчивости путем экспериментального исследования модели и вычисления аналитических оценок ее устойчивости.
2.2 Указания по организации самостоятельной работы
При подготовке к выполнению лабораторной работы необходимо: ознакомиться с постановкой задачи анализа устойчивости моделей; изучить способы оценки устойчивости для моделей в виде систем линейных алгебраических уравнений (СЛАУ); повторить материал по технологии работы с пакетами программ для решения вычислительных задач. С этой целью может быть использован лекционный материал по соответствующим темам, материал, изложенный в рекомендованной литературе [4, с. 12-13; 5; 6, с. 151-155; 7, с. 43-50], а также материал настоящих методических указаний. В качестве модели объекта выступает система линейных уравнений вида
где
Модель с возмущенной матрицей
где Модель с возмущенной правой частью
где В качестве первой оценки устойчивости модели
где Нормы матрицы
где Элементы обратной матрицы
где В качестве второй оценки устойчивости модели
где
где Для оценки максимальных относительных возмущений (погрешностей) решений использовать соответственно соотношения
Порядок выполнения работы
Ознакомиться с помощью преподавателя с особенностями и режимами работы используемых компьютерных средств и пакета программ. Получить у преподавателя вариант задания и дополнительные исходные данные. Варианты заданий приведены в табл. 2.1.
Таблица 2.1 – Значения коэффициентов модели (матрица
Провести анализ исходной модели путем решения СЛАУ вида (2.1). Сформировать и проанализировать модели с возмущенной матрицей (2.2) и правой частью (2.3). При этом Вычислить значение первой оценки устойчивости модели Вычислить значение второй оценки устойчивости модели Провести анализ абсолютной и относительной погрешностей решений для возмущенных моделей. Оценить максимально возможное возмущение решения с помощью отношений (2.11) – (2.12). Сравнить полученные результаты. Сделать выводы, оформить и сдать отчет о выполненной работе. Содержание отчета
Отчет должен содержать: – титульный лист; – цель работы; – математические соотношения для вычисления оценок меры устойчивости модели; – результаты анализа исходной и возмущенных моделей (решений соответствующих СЛАУ); – относительные оценки погрешностей и меры устойчивости модели; – анализ полученных результатов и конкретные выводы по работе, сделанные по результатам проведенных экспериментов.
2.6 Контрольные вопросы и задания
1. Приведите постановку задачи исследования устойчивости модели в виде СЛАУ. 2. Запишите соотношения, определяющие значение первой оценки устойчивости модели 3. Запишите соотношения, определяющие значение второй оценки устойчивости модели 4. Какие матрицы называют плохо обусловленными? 5. Какие матрицы называют хорошо обусловленными? 6. Что показывает мера обусловленности матрицы системы 7. Опишите суть процедуры решения несовместных СЛАУ. Цель работы
Изучение методов решения многокритериальных задач выбора вариантов построения систем управления, использующих выделение области компромиссов и формирование функций полезности решений. Приобретение практических навыков выбора решений с использованием различных схем оптимизации.
3.2 Указания по организации самостоятельной работы
При подготовке к выполнению лабораторной работы необходимо: изучить постановку проблемы многокритериальной оптимизации и основные этапы ее решения; обратить внимание на аргументацию целесообразности выделения области компромиссов (ОК) и приближенной области компромиссов (ПОК); изучить методы формирования ОК и ПОК, разобрать вопросы, связанные с формированием функций полезности (ФП) частных критериев; изучить суть метода выбора решений с использованием лексикографической и универсальной схем оптимизации. С этой целью может быть использован лекционный материал по соответствующим темам, материал, изложенный в рекомендованной литературе [3, c. 17-29; 8, с. 22-28, 54-59, 66-70, 84-86], а также материал настоящих методических указаний. При этом следует обратить внимание на тот факт, что решения, получаемые при использовании различных методов и схем компромисса, в общем случае будут различными.
Описание задачи
В работе рассматривается задача многокритериальной оптимизации в следующей постановке. Каждый вариант построения системы x из множества допустимых X оценивается по множеству частных критериев Необходимо найти оптимальное решение
где opt – оператор оптимизации;
При решении задачи использовать лексикографическую и универсальную схемы оптимизации.
Определение приближенной ОК
Область (множество) допустимых решений X определяется системой ограничений
где
Выделение приближенной области компромиссов
Таблица 3.1 – Результаты оптимизации по частным критериям
Каждая строка табл. 3.1 содержит значения
Формирование ОК
В общем случае приближенная область компромиссов
Порядок выполнения работы
Ознакомиться с помощью преподавателя с особенностями и режимами работы используемых компьютерных средств и пакета программ ModSyst. Получить у преподавателя вариант задания и дополнительные исходные данные. Варианты заданий приведены в табл. 3.2.
Таблица 3.2 – Варианты заданий
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.233.2 (0.016 с.) |

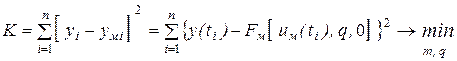 . (1.3)
. (1.3)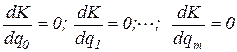 (1.4)
(1.4) (1.5)
(1.5)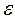 (1.6).
(1.6). ) изменить степень полинома модели и повторно произвести выбор наилучших значений ее параметров qо.
) изменить степень полинома модели и повторно произвести выбор наилучших значений ее параметров qо. , (2.1)
, (2.1) – матрица коэффициентов системы уравнений;
– матрица коэффициентов системы уравнений; – искомый вектор параметров модели;
– искомый вектор параметров модели;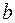 – вектор правой части системы уравнений.
– вектор правой части системы уравнений.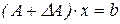 , (2.2)
, (2.2)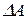 – возмущение матрицы
– возмущение матрицы  , описывающее погрешность определения (задания) ее коэффициентов.
, описывающее погрешность определения (задания) ее коэффициентов.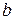 представляется в виде
представляется в виде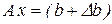 , (2.3)
, (2.3) – возмущение вектора правой части
– возмущение вектора правой части  использовать число обусловленности матрицы
использовать число обусловленности матрицы  =
=  , (2.4)
, (2.4)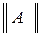 и
и  – соответственно нормы матрицы
– соответственно нормы матрицы  .
. ; (2.5)
; (2.5) ; (2.6)
; (2.6) , (2.7)
, (2.7)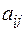 – элемент матрицы
– элемент матрицы  СЛАУ вида
СЛАУ вида , (2.8)
, (2.8) – искомые элементы обратной матрицы;
– искомые элементы обратной матрицы;  =1, если
=1, если  ;
; 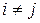 .
. использовать соотношение для симметричных матриц
использовать соотношение для симметричных матриц  , (2.9)
, (2.9) – собственные числа матрицы
– собственные числа матрицы  , (2.10)
, (2.10)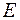 – единичная матрица.
– единичная матрица. ; (2.11)
; (2.11) . (2.12)
. (2.12) 11
11
 .
. , где
, где  – оперативность, выражаемая временем решения задачи управления;
– оперативность, выражаемая временем решения задачи управления;  – надежность, выражаемая посредством коэффициента готовности;
– надежность, выражаемая посредством коэффициента готовности;  – стоимость системы. При этом
– стоимость системы. При этом  ,
, 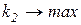 ,
, 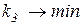 . Известно отображение
. Известно отображение  и относительная важность частных критериев, выраженная, например, вектором весовых коэффициентов
и относительная важность частных критериев, выраженная, например, вектором весовых коэффициентов 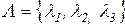 .
. , (3.1)
, (3.1)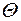 – оператор, определяющий конкретный вид обобщенного критерия.
– оператор, определяющий конкретный вид обобщенного критерия. , i = 1, 2, 3. Область допустимых решений в общем случае состоит их двух подобластей
, i = 1, 2, 3. Область допустимых решений в общем случае состоит их двух подобластей , (3.2)
, (3.2) – область согласия, в которой частные критерии могут изменяться согласовано;
– область согласия, в которой частные критерии могут изменяться согласовано; – область компромиссов, в которой хотя бы одна пара критериев является строго противоречивой.
– область компромиссов, в которой хотя бы одна пара критериев является строго противоречивой. сокращает область поиска решения x и (или) упрощает формирование точной ОК
сокращает область поиска решения x и (или) упрощает формирование точной ОК  \
\ 

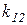
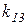




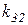
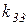
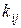 всех частных критериев
всех частных критериев  =
=  ,
, 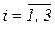 расположены на главной диагонали. Найдя в столбцах наихудшие значения для соответствующих частных критериев
расположены на главной диагонали. Найдя в столбцах наихудшие значения для соответствующих частных критериев 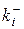 ,
,  , j = 1, 2, 3 в пространстве частных критериев
, j = 1, 2, 3 в пространстве частных критериев  . Решения x из области допустимых решений X, все частные критерии которых имеют значения в полученных границах принадлежат
. Решения x из области допустимых решений X, все частные критерии которых имеют значения в полученных границах принадлежат 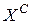 . Если решение x из
. Если решение x из  может быть улучшено по одному или нескольким частным критериям без ухудшения качества по другим, то оно не включается в
может быть улучшено по одному или нескольким частным критериям без ухудшения качества по другим, то оно не включается в  принадлежат
принадлежат  , т.е.
, т.е.  и
и  ,
,  ,…,
,…, 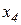 ,… и т.д. и удалении из дальнейшего рассмотрения решений, которые по всем частным критериям хуже других (другого).
,… и т.д. и удалении из дальнейшего рассмотрения решений, которые по всем частным критериям хуже других (другого).







