
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование динамики объектов с помощью аналитических моделейСодержание книги
Поиск на нашем сайте
Цель работы Изучение методов аналитического моделирования динамики объектов, описываемых системами обыкновенных дифференциальных уравнений. Приобретение навыков исследования объектов средствами компьютерного моделирования. Экспериментальная оценка точности определения траектории движения объекта. 4.2 Указания по организации самостоятельной работы При подготовке к выполнению лабораторной работы необходимо: ознакомиться с постановкой задачи исследования моделей динамики объектов в переменных состояния; уяснить суть процедуры преобразования моделей задач, описываемых системами обыкновенных дифференциальных уравнений (ОДУ), к форме Коши; ознакомиться с методами аналитического, численного и качественного исследования моделей динамики в виде систем ОДУ; повторить методы вычисления собственных значений и векторов матриц, а также технологию решения перечисленных задач в среде пакета программ MathCAD или ему подобного. С этой целью может быть использован лекционный материал по соответствующим темам, материал, изложенный в рекомендованной литературе [3, c. 96 – 103; 4, с. 228 – 238; 5], а также материал настоящих методических указаний. Практическая часть подготовки к выполнению работы включает в себя: составление в среде используемого пакета программ модуля для определения собственных значений и векторов матрицы объекта, построения графиков, отражающих модельные траектории, а также заготовки отчета к лабораторной работе.
Описание задачи Модель динамики объекта в форме Коши представляется системой ОДУ вида
где Z(t) – искомая вектор-функция координат (состояний) объекта размерностью n; A – матрица постоянных коэффициентов размерностью В = [b1, b2, …, bn]T – вектор управляющих воздействий;
Z(0) – вектор начальных условий. Необходимо исследовать динамику объекта на отрезке времени При этом считать, что объект функционирует в условиях стабильной помехи, т.е. В процессе выполнения лабораторной работы необходимо решить следующие задачи: 1. Определить начальные условия задачи. 2. Выбрать шаг моделирования и определить траекторию свободного движения объекта методом Рунге-Кутта. 3. Определить траекторию свободного движения объекта аналитическим методом. 4. Оценить точность решения, полученного методом Рунге-Кутта. 5. Методом Рунге-Кутта определить траекторию движения объекта в условиях действия помехи 6. Подобрать значения параметров управляющего воздействия b1, b2,…, bn+1, обеспечивающих изменение координат вектора состояний в заданном диапазоне
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.15 (0.008 с.) |

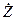 = A Z(t) + B
= A Z(t) + B 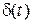 +
+  (4.1)
(4.1) ;
; . В качестве начальных условий Z (t0 ) использовать один из собственных векторов матрицы A (соответствующий вещественному собственному значению и имеющий все ненулевые компоненты).
. В качестве начальных условий Z (t0 ) использовать один из собственных векторов матрицы A (соответствующий вещественному собственному значению и имеющий все ненулевые компоненты). , а функция, реализующая закон управления имеет вид
, а функция, реализующая закон управления имеет вид 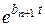 , где
, где 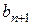 – постоянный коэффициент.
– постоянный коэффициент. ,
,  , где
, где  – соответственно минимальное и максимально допустимые значения i -й координаты состояния.
– соответственно минимальное и максимально допустимые значения i -й координаты состояния.


