
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование процессов выбора решенийСодержание книги
Поиск на нашем сайте
Цель работы
Изучение методов решения многокритериальных задач выбора вариантов построения систем управления, использующих выделение области компромиссов и формирование функций полезности решений. Приобретение практических навыков выбора решений с использованием различных схем оптимизации.
3.2 Указания по организации самостоятельной работы
При подготовке к выполнению лабораторной работы необходимо: изучить постановку проблемы многокритериальной оптимизации и основные этапы ее решения; обратить внимание на аргументацию целесообразности выделения области компромиссов (ОК) и приближенной области компромиссов (ПОК); изучить методы формирования ОК и ПОК, разобрать вопросы, связанные с формированием функций полезности (ФП) частных критериев; изучить суть метода выбора решений с использованием лексикографической и универсальной схем оптимизации. С этой целью может быть использован лекционный материал по соответствующим темам, материал, изложенный в рекомендованной литературе [3, c. 17-29; 8, с. 22-28, 54-59, 66-70, 84-86], а также материал настоящих методических указаний. При этом следует обратить внимание на тот факт, что решения, получаемые при использовании различных методов и схем компромисса, в общем случае будут различными.
Описание задачи
В работе рассматривается задача многокритериальной оптимизации в следующей постановке. Каждый вариант построения системы x из множества допустимых X оценивается по множеству частных критериев Необходимо найти оптимальное решение
где opt – оператор оптимизации;
При решении задачи использовать лексикографическую и универсальную схемы оптимизации.
Определение приближенной ОК
Область (множество) допустимых решений X определяется системой ограничений
где
Выделение приближенной области компромиссов
Таблица 3.1 – Результаты оптимизации по частным критериям
Каждая строка табл. 3.1 содержит значения
Формирование ОК
В общем случае приближенная область компромиссов
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.95.98 (0.01 с.) |

 , где
, где  – оперативность, выражаемая временем решения задачи управления;
– оперативность, выражаемая временем решения задачи управления;  – надежность, выражаемая посредством коэффициента готовности;
– надежность, выражаемая посредством коэффициента готовности;  – стоимость системы. При этом
– стоимость системы. При этом  ,
, 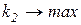 ,
, 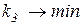 . Известно отображение
. Известно отображение  и относительная важность частных критериев, выраженная, например, вектором весовых коэффициентов
и относительная важность частных критериев, выраженная, например, вектором весовых коэффициентов 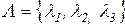 .
. , (3.1)
, (3.1)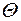 – оператор, определяющий конкретный вид обобщенного критерия.
– оператор, определяющий конкретный вид обобщенного критерия. , i = 1, 2, 3. Область допустимых решений в общем случае состоит их двух подобластей
, i = 1, 2, 3. Область допустимых решений в общем случае состоит их двух подобластей , (3.2)
, (3.2) – область согласия, в которой частные критерии могут изменяться согласовано;
– область согласия, в которой частные критерии могут изменяться согласовано; – область компромиссов, в которой хотя бы одна пара критериев является строго противоречивой.
– область компромиссов, в которой хотя бы одна пара критериев является строго противоречивой. сокращает область поиска решения x и (или) упрощает формирование точной ОК
сокращает область поиска решения x и (или) упрощает формирование точной ОК  \
\ 

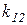
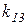




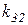
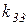
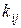 всех частных критериев
всех частных критериев  =
=  ,
, 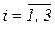 расположены на главной диагонали. Найдя в столбцах наихудшие значения для соответствующих частных критериев
расположены на главной диагонали. Найдя в столбцах наихудшие значения для соответствующих частных критериев 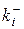 ,
,  , j = 1, 2, 3 в пространстве частных критериев
, j = 1, 2, 3 в пространстве частных критериев  . Решения x из области допустимых решений X, все частные критерии которых имеют значения в полученных границах принадлежат
. Решения x из области допустимых решений X, все частные критерии которых имеют значения в полученных границах принадлежат 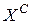 . Если решение x из
. Если решение x из  может быть улучшено по одному или нескольким частным критериям без ухудшения качества по другим, то оно не включается в
может быть улучшено по одному или нескольким частным критериям без ухудшения качества по другим, то оно не включается в  принадлежат
принадлежат  , т.е.
, т.е.  и
и  ,
,  ,…,
,…, 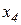 ,… и т.д. и удалении из дальнейшего рассмотрения решений, которые по всем частным критериям хуже других (другого).
,… и т.д. и удалении из дальнейшего рассмотрения решений, которые по всем частным критериям хуже других (другого).


