
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості до контрольної роботи №3 ⇐ ПредыдущаяСтр 8 из 8
Алгебраїчна крива - це множина точок { x,y }, що задовольняє рівняння кривої F(x,y) = 0, де F(x,y) - функція від двох змінних x,y, яка є скінченною сумою виразів виду axnym. Степінь одночлена - це сума степенів змінних. Степінь кривої - це максимальна з степенів її одночленів. Нехай на площині 1) Неявне визначення: 2) Явне визначення: 3) Параметричне визначення: 4) Векторне визначення Інтерполяція поліномами Лагранжа на площині Задані (n+1) різні точки Pk =Pk (xk,yk) і значення параметра t (t0<t1<…<tn), які відповідають цим точкам. Знайти поліномну вектор-функцію Розв’язок цієї задачі можна шукати по кожній координаті окремо, як розв'язок відповідної інтерполяційної задачі: знаходження
Скористаємось векторним записом розв’язку з використанням поліномів Лагранжа
де
При цьому Lk(t) = 1 на k -тому вузлі, на інших вузлах Lk(t) = 0.
Зауваження 6. Параметр
Криві Без’є На початку розвитку комп’ютерної графіки дуже гострою була задача представлення кривих у памяті ЕОМ. У 1970 році П'єр Без’є запропонував метод зображення кривої, який достатно зручний як з точки зору машинного представлення, так і для використання художниками та дизайнерами як робочий інструмент.
Функція f(n), n=0,1,2,…, яка задовольняє рекурентному співвідношенню Для будь-якого n ≥0 маємо Для будь-яких невід’ємних
має назву біноміального коефіцієнту(числа сполук з Наведемо деякі властивості сполук: 1)
Визначимо базові поліноми Бернштейна
Крива Без’є визначається вершинами Pk (k = 0,1,…, n) базового багатокутника, який однозначно визначає положення кривої на площині або у просторі. Для побудови кривої Без’є використовуємо поліноми Бернштейна і вершини Pk(xk,yk), k = 0,1,…, n, тобто крива Без’є має вигляд:
де рn,k(t) - к -та функція базису Бернштейна порядку n, її максимумдосягається при t=k/n.
Або через компоненти
Легко побачити, що кожну з цих компонент можна підраховувати окремо, як поліном Бернштейна для відповідної координатної функції від параметра t.
Якщо треба додержуватись неперервності кривизни і нахилу у точках з’єднання кривих, то треба знайти і першу, і другу похідні кривої Без’є. Теорема. Для кривої Без’є (2) маємо наступні співвідношення 1) 2) 3) 4) Розглянемо умови неперервності сусідніх кривих Без’є. Нехай маємо дві криві Без’є з базовими багатокутниками відповідно P0,P1,…,Pn і Q0,Q1,…,Qm. Умова співпадання кінцевої точки першої кривої Без’є з початковою точкою наступної кривої
Для співпадання напрямків дотичних у точці переходу необхідна умова
При Умова
(вектори йдуть уздовж діагоналі паралелограма, що побудований на двох останніх відрізках першого характеристичного багатокутника і на двох перших відрізках другого характеристичного багатокутника).
На практиці часто розглядають базовий чотирикутник, для якого
і рівняння кривої Без’є приймає вигляд:
або
Легко бачити, що при
Для того, щоб при спряженні двох кривих Без’є з характеристичними чотирикутниками
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.251.155 (0.008 с.) |
 зафіксована нормальна система координат. Крива на площині може мати
зафіксована нормальна система координат. Крива на площині може мати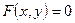 ;
; або
або  ;
; .
.
 ), де
), де  - поліноми n -го степеня, яка проходить через ці точки, тобто r(tk)=Pk.
- поліноми n -го степеня, яка проходить через ці точки, тобто r(tk)=Pk. , для якого
, для якого  , і знаходження
, і знаходження  , для якого
, для якого  .
.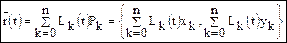 ,
, - елементарні поліноми Лагранжа - визначено за формулами
- елементарні поліноми Лагранжа - визначено за формулами 
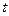 можна інтерпретувати як деяку міру довжини переміщення уздовж кривої. Але ототожнювати його з відстанню уздовж кривої не можна. У більшості випадків цей параметр інтерпретують як час переміщення уздовж кривої, але це переміщення не є рівномірним.
можна інтерпретувати як деяку міру довжини переміщення уздовж кривої. Але ототожнювати його з відстанню уздовж кривої не можна. У більшості випадків цей параметр інтерпретують як час переміщення уздовж кривої, але це переміщення не є рівномірним. ,
,  , має назву факторіала числа
, має назву факторіала числа  і позначається
і позначається 
 .
. функція
функція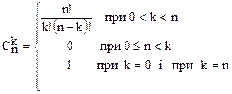
 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 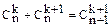
 .
. (2)
(2) . (3)
. (3) (Точка
(Точка  є початковою точкою кривої Без’є).
є початковою точкою кривої Без’є). ( Точка
( Точка  є кінцевою точкою кривої Без’є ).
є кінцевою точкою кривої Без’є ).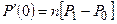 ,
,  (Вектор
(Вектор  визначає напрямок дотичноговектора до кривої Без’є у початковій точці, а вектор
визначає напрямок дотичноговектора до кривої Без’є у початковій точці, а вектор  - у кінцевій).
- у кінцевій).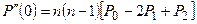 ,
,  - другі похідні визначаються двома суміжними граничними сегментами базового багатокутника (три найближчі вершини).
- другі похідні визначаються двома суміжними граничними сегментами базового багатокутника (три найближчі вершини). (4)
(4) , де
, де  - скалярний множник. Тобто
- скалярний множник. Тобто  або, якщо врахувати (4),
або, якщо врахувати (4),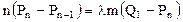 .
. одержуємо Pn – Pn-1 = λ(Q1 – Pn). Якщо ще накласти умову, щоб дотичні вектори у точці переходу були однакові (тобто
одержуємо Pn – Pn-1 = λ(Q1 – Pn). Якщо ще накласти умову, щоб дотичні вектори у точці переходу були однакові (тобто  ), то маємо співвідношення для умови неперервності перших похідних Q1+Pn-1=2Pn, яке означає, що точка
), то маємо співвідношення для умови неперервності перших похідних Q1+Pn-1=2Pn, яке означає, що точка  є середньою точкою відрізка
є середньою точкою відрізка 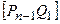 . При цьому
. При цьому  .
. дає співвідношення для умови неперервності других похідних:
дає співвідношення для умови неперервності других похідних:
 . У цьому випадку маємо:
. У цьому випадку маємо: ,
,  ,
, ,
, 

 .
.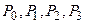 є кубічний сплайн з початковою точкою
є кубічний сплайн з початковою точкою  і напрямками дотичних у кінцевих точках, що проходять відповідно через точки
і напрямками дотичних у кінцевих точках, що проходять відповідно через точки  і
і  (тобто визначаються сторонами
(тобто визначаються сторонами  і
і  характеристичного чотирикутника).
характеристичного чотирикутника). були неперервні дотичні вектори у точках переходу
були неперервні дотичні вектори у точках переходу  , необхідно щоб відрізки
, необхідно щоб відрізки  були рівні і паралельні.
були рівні і паралельні.


