Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості до контрольної роботи №2.
Лінійна система координат на площині визначається заданням двох не паралельних прямих l1 і l2, що мають точку перетину О. На кожній з прямих визначимо масштаб. Щоб визначити координати довільної точки М, треба провести прямі l1* і l2*, паралельні прямим l1 і l2. Тоді координати точки М визначаються за відрізками х1 і х2 на прямих l1 і l2, що відтинаються прямими l1* і l2*. Тоді всю площину можна розглядати як двовимірний векторний простір R2. Координати вектора
Точка на площині представляється двома координатами у вигляді вектора-стовпця або вектора-рядка. Надалі для зображення точки будемо користуватись вектором-рядком Х=[ x y ], а для зображення множини точок (об"єкта на площині) матрицею, кожний рядок якої відповідає зображенню однієї точки, що належить цьому об"єкту. Ця множина зберігається в комп"ютері у вигляді матриці або масиву чисел. Лінії, що з"єднують точки, формують зображення об"єкта. Перетворення об"єкта (множини точок) здійснюється за допомогою матриці, яку можна інтерпретувати як геометричний оператор. Тоді для геометричного перетворення точок використовується множення матриць.
Розглянемо результати множення матриці [ x y ] на матрицю загального перетворення розмірності 2´2:
1) 2) Пряму можна визначити за допомогою двох векторів, що задають координати її кінцевих точок А і В: (хА,уА) і (хВ,уВ), а відрізок АВ можна представити матрицею розміром 2´2: L=
Можна показати, що при афінних перетвореннях: а) середина відрізку перетворюється у середину відрізку, б) паралельні лінії - у паралельні, в) прямі, що перетинаються - у прямі, що перетинаються.
Однорідні координати неоднорідного координатного вектора [ x y ] є трійка чисел [ x' y' h ], де x = x'/h, y = y'/h, а h - деяке дійсне число. Завжди існує один набір координат виду [ x y 1], і це дозволяє представити координатний вектор [ x y ] на фізичній площині XY. Всі інші однорідні координати вектора [ x y ] представляються у вигляді [ hx hy h ], вони не однозначні, наприклад, координати [6 4 2], [12 8 4], [3 2 1] представляють на площині фізичну точку (3,2). Однорідні координати звичайної точки Х на площині - це трійка чисел { x1,x2,х3 }, для яких x3 ¹ 0 і виконуються умови однорідності: для будь-якої пари однорідних координат { x1,x2,х3 }, { y1,y2y3 } точки X існує число t > 0 таке, що y1=tx1, y2=tx2, y3=tx3. Матриця перетворення для однорідних координат на площині має розмір 3´3:
де m і n є координати вектора зсуву у напрямках x і y відповідно. За допомогою цієї матриці можуть бути перетворені всі точки площини, в тому числі і початок координат. Вектор з однорідною компонентою h = 0 - це точка нескінченності.
У даному викладі використовується правостороння система координат, об’єкт обертається відносно нерухомої координатної системи і координатні вектори представлені у вигляді матриці-рядка. Так як вектор задається рядком матриці, то матрицю перетворення треба писати після матриці координатних векторів (множення на матрицю справа). Для обертання навколо початку координат на кут θ маємо:
При обертанні у протилежному напрямку необхідно у (1) замінити q на -q. Тоді (1) буде мати вигляд:
Композиція перетворень - це послідовна дія на координату х базових координатних перетворень Р1 і Р2 у послідовності справа наліво (Р2°Р1)(Х) = Р2(Р1(Х)). Композиції перетворень P2 і Р1, що визначається формулою (Р2×P1)(X) = Р2(P1(X)), відповідає добуток матриць [P1] і [P2] у зворотному порядку. Щоб здійснити перетворення матриці [G] однорідних координат точок при композиції декількох перетворень, потрібно знайти матрицю [R] композиції цих перетворень (при множенні матриць перетворень у зворотному порядку), а потім помножити матрицю координат фігури [G] на знайдену матрицю [R] справа, тобто [G']=[G][R], де [G'] - матриця перетворених координат.
Нехай на площині p фіксована деяка світова система лінійних координат. Для будь-якого лінійного перетворення А координатне представлення має вигляд (A): x'=xa+b, Дія лінійного перетворення у матричному вигляді: [ x' ] = [ x ]∙[A], або у однорідних координатах [ x1',x2',x3' ] = [ x1,x2,x3 ]∙ Матриця s (А) = [A] =
Таблиця 7- Базові перетворення площини
Наведемо деякі співвідношення між описаними перетвореннями:
Tb° Ta=Ta+bTm° T-m=E(Tm)-1=T-m SA° SA=E SOТm=T-mSO(SA)-1=SA
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.126.74 (0.011 с.) |
 . Якщо осі перпендикулярні, то маємо декартову систему координат, яку надалі і будемо використовувати. Для світових координат (кут між осями 90˚ і масштаб вздовж осей однаковий) | MN |2= (x1-x2) 2+ (y1-y2) 2.
. Якщо осі перпендикулярні, то маємо декартову систему координат, яку надалі і будемо використовувати. Для світових координат (кут між осями 90˚ і масштаб вздовж осей однаковий) | MN |2= (x1-x2) 2+ (y1-y2) 2. . Послідовно надаючи а,b,с і d різних значень, знайдемо матриці, що відповідають різним перетворенням точки. Наприклад,
. Послідовно надаючи а,b,с і d різних значень, знайдемо матриці, що відповідають різним перетворенням точки. Наприклад, , отже x'=a∙x - результат масштабування координати х,
, отже x'=a∙x - результат масштабування координати х, - зсув координатного вектора.
- зсув координатного вектора. . Щоб одержати перетворені координати векторів (точок) [A'] і [B'], треба помножити матрицю L на матрицю перетворення T: [L]×[T]=[L']. Пряма при такому перетворенні перетворюється у пряму, і всі точки перетвореної лінії безпосередньо відповідають всім точкам висхідної лінії.
. Щоб одержати перетворені координати векторів (точок) [A'] і [B'], треба помножити матрицю L на матрицю перетворення T: [L]×[T]=[L']. Пряма при такому перетворенні перетворюється у пряму, і всі точки перетвореної лінії безпосередньо відповідають всім точкам висхідної лінії. ,
,
 (1).
(1). .
. ÎM2, x',x,b ÎR2, або (A):
ÎM2, x',x,b ÎR2, або (A):  . У однорідних координатах (А):
. У однорідних координатах (А):  .
. .
. – це головний символ перетворення, а величина c(А) = det([A]) - характер перетворення. Якщо c(А) ≠ 0, то перетворення А є афінним: А Î Aff(π), де Aff(π) – множина афінних перетворень на площині.
– це головний символ перетворення, а величина c(А) = det([A]) - характер перетворення. Якщо c(А) ≠ 0, то перетворення А є афінним: А Î Aff(π), де Aff(π) – множина афінних перетворень на площині.



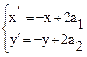

 - cиметрія відносно осі абсцис
- cиметрія відносно осі абсцис


 - cиметрія відносно осі ординат
- cиметрія відносно осі ординат




 - гомотетія відносно початку координат
- гомотетія відносно початку координат


 - центральна гомотетія відносно точки А(а1,а2)
- центральна гомотетія відносно точки А(а1,а2)


 - гомотетія до осі абсцис
- гомотетія до осі абсцис


 - гомотетія до осі ординат
- гомотетія до осі ординат
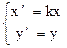

 -множинно-осьова гомотетія
-множинно-осьова гомотетія


 - осьова гомотетія відносно прямої (l): l 1x+ l 2y+ l 3=0 (l 12+ l 22=1)
- осьова гомотетія відносно прямої (l): l 1x+ l 2y+ l 3=0 (l 12+ l 22=1)


 -обертання навколо початку координат на кут
-обертання навколо початку координат на кут 


 - обертання навколо точки А(а1,а2) на кут
- обертання навколо точки А(а1,а2) на кут  ,
де
,
де