
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила выполнения переходов в сети Петри. Основные задачи моделирования.Содержание книги
Поиск на нашем сайте Правила переходов в сети Петри: 1) Если для перехода выполнены предусловия, т.е. переход является выполнимым, то после его осуществления, может быть изменена разметка. Она меняется => образом: по каждой входной дуге число меток уменьшается на 1, по каждой выходной увелич на 1.
=> сеть остановилась => отсутвуют условия условия повторного запуска. 2) переходы могут запускаться не только последовательно но и параллельно //Нарисовать рисунок с 3мя шариками и 4мя переходами и описать словами параллельные запуски) Если в шарике не остается точек то система умирает.
Состояние сети характеризуется разметкой в данный момент времени и в результате запусков переходов эта разметка меняется. Т.о. можно представить сеть Петри как систему векторов разметок и их изменений или систему сложения векторов.
m1, m2 – число меток в соотв позициях. В каждый данный момент можно представить разметку в виде вектора Возникают 2 типа задач: 1 Достижимости, - заключается: можно ли с помощью этих векторов сконструировать переход? Она решается с помощью теоремы отделимости: Теорема: у можно представить в виде линейной комбинации х1, х2, …., если нет разделяющей плосткости (вектора лежат по одну сторону от раздел плоскости, а требуемый вектор по другую, т.е. такой лин комбинации нет)). 2 Проблема живучисти – т-ма недостижимости нуля: достижим ли ноль из данной позиции. Какие то переходы всегда будут запускаемыми. Рекуррентное соотношение
Чтобы получить В рез-те запуска некоторые метки исчезнут, они будут описываться матрицей
D = D+ - D-- = [ …. Вычесть и написать … ], т.е. 40. На низком уровне вычислительные системы могут быть описаны автоматами. Автомат — это пятерка (Q, ∑, ∆, δ, Г), где Q — конечное множество состояний {q1, q2,…, qk}; ∑ — конечный входной алфавит; ∆ — конечный выходной алфавит;δ: Q х ∑ → Q — функция следующего состояния, отображающая текущее состояние и текущий вход в следующее состояние; Г: Q х ∑→∆ — функция выхода, отображающая текущее состояние и текущий вход в выходной символ. Автоматы часто представляют в виде графов переходов, как, например, на рис. 3.9. В графе переходов состояния представляются кружками, являющимися вершинами. Дуга из состояния qi в qj помеченная a|b, означает, что, находясь в состоянии qi автомат при входе а перейдет в состояние qj выдавая при этом символ b. Формально следовало бы записать δ(qi,a)=qj и Г (qi,a)=b Входной алфавит определяет входы автомата из внешнего мира, а выходной алфавит — выходы автомата во внешний мир. В качестве примера рассмотрим автомат, изображенный на рис. 3.9. Этот автомат преобразует двоичное число, представленное последовательностью бит, начиная с младшего, в дополнение до двух. В данном случае входной и выходной алфавит состоит из трех символов: 0, 1 и R. Автомат начинает работать в состоянии qt. Символ сброса (R) означает конец (или начало) числа и возвращает автомат в исходное состояние. Выход автомата для символа сброса является просто его повторением.
Аналогичный автомат показан на рис. 3.10. При тех же самых входах этот автомат вычисляет четность входного числа. Он начинает работу в состоянии q1. Выход копирует вход до тех пор, пока входным символом не окажется символ сброса. Выходом для символа сброса будет 0 в случае нечетного числа и 1 — в случае четного числа. При представлении конечного автомата сетью Петри следует обратить внимание на связь между сетью Петри и внешним миром, которая ранее не учитывалась. Моделирование взаимодействия с внешним миром можно реализовать многими способами. В нашей задаче мы моделируем это взаимодействие с помощью специального множества позиций. Позициями будут представлены каждый входной и выходной символы. Мы допускаем, что из внешнего мира помещается фишка в позицию, соответствующую входному символу, а затем фишка, появившаяся в позиции, соответствующей выходному символу, удаляется оттуда. Эта последовательность действий будет повторяться необходимое число раз. Общая схема проиллюстрирована на рис. 3.11. Заметим, что здесь не исключена возможность путаницы в понятиях, так как позиции, соответствующие входным и выходным символам, могут быть обоснованно названы входными и выходными Позициями сети. Однако их не следует путать с входными или вы-
ходными позициями переходов. Несмотря на возможную путаницу, эти термины наиболее естественны для обоих понятий. В качестве альтернативного подхода к моделированию входов и выходов сети могут быть использованы переходы. Для определения следующего входного символа из внешнего мира следует выбирать входной переходи запускать его. Сеть Петри ответит (в конце концов) запуском соответствующего перехода из множества выходных переходов, связанного с соответствующим выходом. Затем из внешнего мира будет запущен новый входной переход и т. д. Этот подход проиллюстрирован на рис. 3.12. Нетрудно показать, что оба этих подхода эквивалентны, поэтому будем использовать первый из них, в котором входные и выходные символы моделируются позициями. Задав представление позиций, соответствующих символам входа и выхода, мы можем завершить построение модели системы конечных состояний. Представим каждое состояние автомата позицией в сети Петри. Текущее состояние отмечается фишкой; все остальные позиции пусты. Теперь для определения переходов из состояния в состояние можно ввести переходы сети следующим образом. Для каждой пары (состояние и входной символ) мы определяем переход, входными позициями которого являются позиции, соответствующие состоянию и входному символу, а выходными позициями — позиции, соответствующие следующему состоянию и выходу.
Для конечного автомата (Q, ∑, ∆, δ, Г) мы определили сеть Петри (Р, Т, I, О) таким образом: P = Q T = {tq,σ|q I(tq,σ) ={q,σ}, O(tq,σ) = {δ(q,σ), Г(q,σ)} Эта сеть Петри является моделью конечного автомата. На рис. 3.13 изображена сеть Петри, соответствующая автомату с рис. 3.9. На рис. 3.14 - cеть Петри, соответствующая автомату с рис. 3.10. При сравнении сетей Петри на рис. 3.13, 3.14 с эквивалентными автоматами на рис. 3.9, 3.10 возникают некоторые вопросы. Прежде всего: почему модель сети Петри предпочтительнее описания конечным автоматом? Описание автоматом более понятно, чем описание сетью Петри, в которой 6 переходов, 24 дуги и 7 или 8 позиций. Это верно. Однако мы показали, что сети Петри могут представлять любую систему, представимую автоматом, и это свидетельствует о больших возможностях сетей Петри. Кроме того, следует отметить, что модель сети Петри имеет определенное преимущество при композиции автоматов. Например,
заметим, что выходной алфавит автомата с рис. 3.9 идентичен входному алфавиту автомата с рис. 3.10. Передавая выход автомата с рис. 3.9 на вход автомата с рис. 3.10, можно построить композицию автоматов, вычисляющую дополнение до двух и проверяю
щую четность. Такая композиция является автоматом с составными состояниями, компоненты которых — это состояния обоих подавтоматов. В сетях Петри такая композиция есть просто совмещение выходных позиций первой сети с входными позициями второй. На рис. 3.15 показана композиция автоматов, а на рис. 3.16 — составная сеть Петри. Другое преимущество представления сети Петри связано с иными формами композиции. Например, параллельная композиция позволяет компонентам композиции автоматов работать одновременно. В этом случае вновь получаем автомат с составными состояниями, в то время как для сети Петри — это просто дублирование фишек во входах, соответствующих входным символам, и использование их во всех компонентах сети Петри. Наконец, на выходе мы просто выбираем соответствующие позиции выхода. Например, если мы хотим соединить параллельно две сети Петри (рис. 3.13 и 3.14), то в результате получим сеть Петри, подобную изображенной на рис. 3.17, которая вычисляет дополнение числа до двух и его четность. Если на входе появляется символ сброса, то выходом является четность.
41. матричное описание поведения сети Петри в пространстве разметок Сети Петри (N - схемы). Сети Петри является эффективным инструментом моделирования сложных иерархических дискретных систем. Они позволяют отображать асинхронность, параллелизм и иерархичность моделируемых объектов более просто, чем другие средства моделирования. Основные определения: N=(P, T, F, H, μ0), P – конечное непустое множество позиций (состояний, мест),
F: P*T->{0, 1, 2, …} – функция входных инциденций. H: T*P->{0, 1, 2, …} – функция выходных инциденций. μ0: P->{0, 1, 2, …} – начальная маркировка (размерка сети) Сеть Петри графически представляется в виде двудольного ориентированного графа с двумя типами вершин
p={p1,p2, p3, p4, p5} T={t1,t2, t3, t4}
(·p) – множество входных переходов для позиций (p·) – множество выходных переходов для позиций (·t) – множество входных позиций (t·) – множество выходных позиций (·p1)=(t2, t3); (·t1)=(p1, p2) (p1·)=t1 ; (t1·)=(p3, p4) μ0=(1, 1, 0, 0, 0)
Если мощность множества P=n, то маркеровку можно представить n-мерным вектором, координаты которого = числу маркеров соответствующих позиций. Переход от одной маркировки к другой выполняется по средствам срабатывания переходов. Переход t может сработать при маркировке μ(p), если он является возбужденным, то есть, если выполняется условие μ(p)-F(p,t)≥0,
1) Маркировка 2) Маркировка 3) Если при некоторой маркировки ни один из переходов не может сработать, то такая маркировка называется тупиковой. Функционирование Сети Петри – это последовательная схема маркировок в результате срабатывания возбужденных переходов. Графом достижимости называется граф, вершинами которого являются все возможные маркировки. Фрагмент графа достижимости:
В Сети Петри два возбужденных невзаимодействующих перехода могут сработать независимо друг от друга. Поэтому моделям свойствен параллелизм или одновременность. Сети Петри. Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками
— метки.
Сети Петри — математический аппарат для моделирования динамических дискретных систем. Впервые описаны Карлом Петри в 1962 году.
Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами, вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.
Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, разновременно при выполнении некоторых условий.
42. Сеть Петри как система сложения векторов в пространстве разметок и интерпритация проблемы достижимости и живучести. Сети Петри является эффективным инструментом моделирования сложных иерархических дискретных систем. Они позволяют отображать асинхронность, параллелизм и иерархичность моделируемых объектов более просто, чем другие средства моделирования. Основные определения: N=(P, T, F, H, μ0), P – конечное непустое множество позиций (состояний, мест), T – конечное непустое множество переходов F: P*T->{0, 1, 2, …} – функция входных инциденций. H: T*P->{0, 1, 2, …} – функция выходных инциденций. μ0: P->{0, 1, 2, …} – начальная маркировка (размерка сети) Сеть Петри графически представляется в виде двудольного ориентированного графа с двумя типами вершин
T={t1,t2, t3, t4}
(·p) – множество входных переходов для позиций (p·) – множество выходных переходов для позиций (·t) – множество входных позиций (t·) – множество выходных позиций (·p1)=(t2, t3); (·t1)=(p1, p2) (p1·)=t1 ; (t1·)=(p3, p4) μ0=(1, 1, 0, 0, 0)
Если мощность множества P=n, то маркеровку можно представить n-мерным вектором, координаты которого = числу маркеров соответствующих позиций. Переход от одной маркировки к другой выполняется по средствам срабатывания переходов. Переход t может сработать при маркировке μ(p), если он является возбужденным, то есть, если выполняется условие μ(p)-F(p,t)≥0,
1) Маркировка 2) Маркировка 3) Если при некоторой маркировки ни один из переходов не может сработать, то такая маркировка называется тупиковой. Правила переходов в сети Петри: 1) Если для перехода выполнены предусловия, т.е. переход является выполнимым, то после его осуществления, может быть изменена разметка. Она меняется => образом: по каждой входной дуге число меток уменьшается на 1, по каждой выходной увелич на 1.
=> сеть остановилась => отсутвуют условия условия повторного запуска. 2) переходы могут запускаться не только последовательно но и параллельно //Нарисовать рисунок с 3мя шариками и 4мя переходами и описать словами параллельные запуски) Если в шарике не остается точек то система умирает.
Состояние сети характеризуется разметкой в данный момент времени и в результате запусков переходов эта разметка меняется. Т.о. можно представить сеть Петри как систему векторов разметок и их изменений или систему сложения векторов.
m1, m2 – число меток в соотв позициях. В каждый данный момент можно представить разметку в виде вектора Возникают 2 типа задач: 1 Достижимости, - заключается: можно ли с помощью этих векторов сконструировать переход? Она решается с помощью теоремы отделимости: Теорема: у можно представить в виде линейной комбинации х1, х2, …., если нет разделяющей плосткости (вектора лежат по одну сторону от раздел плоскости, а требуемый вектор по другую, т.е. такой лин комбинации нет)). 2 Проблема живучисти – т-ма недостижимости нуля: достижим ли ноль из данной позиции. Какие то переходы всегда будут запускаемыми. Рекуррентное соотношение
Чтобы получить В рез-те запуска некоторые метки исчезнут, они будут описываться матрицей
D = D+ - D-- = [ …. Вычесть и написать … ], т.е.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |



 -вектор разметки
-вектор разметки
 надо вектор запуска (х1,х2,х3). Вектор запуска не дает четкой последовательности запуска, возможностей может быть несколько.
надо вектор запуска (х1,х2,х3). Вектор запуска не дает четкой последовательности запуска, возможностей может быть несколько.

 - что будет изываться
- что будет изываться

 - что будет вновь помещено поле запуска перехода.
- что будет вновь помещено поле запуска перехода.




 ∑
∑ 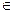 и σ
и σ 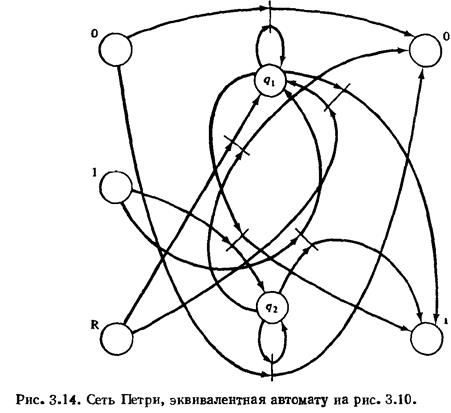

 T – конечное непустое множество переходов
T – конечное непустое множество переходов . Дуги соответствуют функциям инцидентности. Маркировка отражается наличием или отсутствием в позиции точек, которые называют маркерами.
. Дуги соответствуют функциям инцидентности. Маркировка отражается наличием или отсутствием в позиции точек, которые называют маркерами. . Это означает, что в каждой входной позиции перехода t число маркеров не должно быть меньше веса дуги, соединяющей эту позицию с переходом. В результате срабатывания возбужденного перехода маркировка μ(p) замещается на маркировку μ,(p) по следующему правилу:
. Это означает, что в каждой входной позиции перехода t число маркеров не должно быть меньше веса дуги, соединяющей эту позицию с переходом. В результате срабатывания возбужденного перехода маркировка μ(p) замещается на маркировку μ,(p) по следующему правилу: ,
,  непосредственно достижима из маркировки
непосредственно достижима из маркировки  :
: 
 , что
, что 


 p={p1,p2, p3, p4, p5}
p={p1,p2, p3, p4, p5}




