
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
N-канальная СМО с отказами. Основные соотношения.
Рассмотрим на примере 2 канальной системы с 2 местами в очереди.
S1 –1 канал занят, очереди нет S2 – 2 канала занято, очереди нет S3 – 2 канала занято, 1 в очереди S4 – 2 канала занято, 2 в очереди
Лямбда – интенсивность поступления заявок, Время обслуживания Тобс = 1/Мю
Pотказа = Относительная пропускная способность: Q = 1 - Pотказа Среднее число занятости канала: P1 = Lсист =
tсист и tоч – формулы Литтла
число занятых каналов: Вывод формулы Эрланга Рассмотрим систему, которая может обслуживать одновременно m требований. Будем считать, что имеется m линий и очередное требование поступает на одну из линий, если хотя бы одна из них свободна; в противном случае поступающее требование получает отказ и уходит из сферы обслуживания. Предположим, что поток требований является пуассоновским с параметром Рассмотрим состояния k=0,1,…,m, где состояние k означает, что занято ровно k линий. Переход системы из состояния в состояние с течением времени t представляет собой марковский процесс, плотности перехода которого имеют вид
Действительно, переход из k в k+1 осуществляется при поступлении очередного требования, что происходит за время Вероятность того, что ни одна из k занятых линий не освободится за время Вероятность других изменений в системе за промежуток времени Стационарные вероятности
Из этих уравнений получаем, что
Найденные выражения для стационарных вероятностей называются формулами Эрланга. Вывод формул Литтла. Выведем одну важную формулу, связывающую (для предельного стационарного режима) среднее число заявок Lсист, находящихся в системе массового обслуживания (т. е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе Wсист.
Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею 2 потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность λ. Обозначим: Х(t)—число заявок, прибывших в СМО до момента t, Y(t) — число заявок, покинувших СМО до момента t.
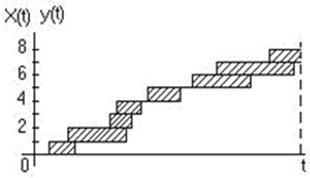
И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (У(t)). Вид функций X(t) и У(t) показан на рис.1; обе линии — ступенчатые, верхняя — X(t), нижняя — Y(t). Очевидно, что для любого момента t их разность Z(t) = Х(t) —Y(t) есть не что иное, как число заявок, находящихся в СМО. Когда линии X(t) и У(t) сливаются, в системе нет заявок. Рассмотрим очень большой промежуток времени Т (мысленно продолжив график далеко за пределы чертежа) и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала Т:
Но этот интеграл представляет собой не что иное, как площадь фигуры, заштрихованной на рис.1. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена t1, t2,... Правда, в конце промежутка Т некоторые прямоугольники войдут в заштрихованную фигуру не полностью, а частично, но при достаточно большом Т эти мелочи не будут играть роли. Таким образом, можно считать, что
Разделим и умножим правую часть на интенсивность λ: Но величина Т λ есть не что иное, как среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен t на среднее число заявок, то получим среднее время пребывания заявки в системе Wсист. Итак, L= λ W, откуда Wсист = Lсист / λ. (1)
Это и есть замечательная формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок. Точно таким же образом выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди Wоч и среднее число заявок в очереди Lоч: Wоч =Lоч / λ. Для вывода достаточно вместо нижней линии из рис.1 взять функцию U(t) — количество заявок, ушедших до момента Т не из системы, а из очереди (если заявка, пришедшая в систему, не становится в очередь, а сразу идет под обслуживание, можно все же считать, что она становится в очередь, но находится в ней нулевое время). Формулы Литтла играют большую роль в теории массового обслуживания.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.95.244 (0.006 с.) |
 S0 – система в режиме ожидания
S0 – система в режиме ожидания
 - приведенная интенсивность (кол-во заявок приходящих в систему в реднем за среднее время обслуживания одной заявки)
- приведенная интенсивность (кол-во заявок приходящих в систему в реднем за среднее время обслуживания одной заявки)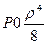
 P0; P2 =
P0; P2 =  ; P3 =
; P3 = 
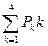 ; Lоч =
; Lоч = 
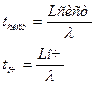 - среднее время нахождения заявки с системе, и среднее время в очереди (tоч)
- среднее время нахождения заявки с системе, и среднее время в очереди (tоч)
 , требования обслуживаются независимо и время обслуживания каждого требования (на каждой из m линий) распределено по показательному закону с параметром
, требования обслуживаются независимо и время обслуживания каждого требования (на каждой из m линий) распределено по показательному закону с параметром  .
.

 с вероятностью
с вероятностью  .
.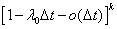 (поскольку линии обслуживаются независимо одна от другой) и вероятность освобождения одной из линий, т.е. перехода из состояния k в k-1 есть
(поскольку линии обслуживаются независимо одна от другой) и вероятность освобождения одной из линий, т.е. перехода из состояния k в k-1 есть 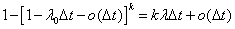 .
. .
. могут быть найдены из уравнений:
могут быть найдены из уравнений: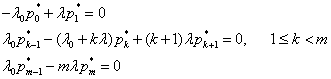


 , где сумма распространяется на все заявки, пришедшие за время Т.
, где сумма распространяется на все заявки, пришедшие за время Т. .
.


