
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
За каждую итерацию выполняется до четырех команд: два сравнения, одна операция увеличения и одна передача управления.Содержание книги
Поиск на нашем сайте
Для ускорения внутреннего цикла общим приемом является добавление в таблицу специальных строк, которые делают необязательной явную проверку того, достиг ли указатель границ таблицы. Это можно сделать в алгоритме 13.1. Если перед поиском мы добавим искомое имя  1while z 1while z  xi do i xi do i  i+1if i i+1if i  n then{найдено: i указывает на z} else{не найдено} n then{найдено: i указывает на z} else{не найдено}
Улучшение алгоритма 1 будет наиболее очевидным, если мы перепишем алгоритм 13.2 в тех же близких к языку машины обозначениях, которые использовались раньше:
 1 цикл: if z = xi then goto возможно i 1 цикл: if z = xi then goto возможно i  i+1 i+1
 n then {найдено:i указывает на z} else{не найдено} n then {найдено:i указывает на z} else{не найдено} При каждой итерации выполняются лишь три действия вместо четырех, как это было в алгоритме 1. Таким образом, в большинстве вычислительных устройств цикл в алгоритме 2 будет выполняться гораздо быстрее, чем в алгоритме 13.1, и поскольку скорость цикла определяет скорость всей программы, такое же сравнение имеет место для двух программ. Печально то, что фокус с добавлением Единственным недостатком алгоритма 2 является то, что при безуспешном поиске (поиске имен, которых нет в таблице) всегда просматривается вся таблица. Если такой поиск возникает часто, то имена надо хранить в естественном порядке; это позволяет завершать поиск, как только при просмотре попалось первое имя, большее или равное аргументу поиска. В этом случае в конец таблицы следует добавить фиктивное имя  1 while z > xi do i 1 while z > xi do i  i+1if z=xi then{найдено:i указывает на z} else{не найдено} i+1if z=xi then{найдено:i указывает на z} else{не найдено}
Лекция № 4 Логарифмический поиск в статических таблицах. Бинарный поиск. Оптимальные деревья бинарного поиска. Логарифмический поиск в динамических таблицах. Логарифмический поиск в статических таблицах Мы говорим о логарифмическом времени поиска, как только возникает возможность за время Самыми распространенными предположениями, которые дают возможность уменьшить размер таблицы от В этом разделе мы рассматриваем только статические таблицы, то есть таблицы, в которых включение и исключение либо не встречаются, либо так редки, что когда они появляются, строится новая таблица. Динамические структуры таблиц, допускающие логарифмическое время поиска, так же как и эффективные алгоритмы включения и исключения, обсуждаются в конце этой лекции. Для статических таблиц нужно обсудить лишь алгоритмы поиска и построения таблицы. Алгоритмы поиска достаточно просты, но некоторые из алгоритмов построения таблицы сложны. Такая ситуация возникает потому, что в случае статической таблицы разумно считать частоты обращения известными, и, может быть, стоит затратить существенные усилия на построение оптимальной таблицы – таблицы с минимальным средним временем поиска (относительно данных частот обращения). Алгоритмы построения таблиц и их анализ являются наиболее важными темами этого раздела. Бинарный поиск Когда ячейки таблицы последовательно распределены в памяти с произвольным доступом и имена хранятся в таблице в их естественном порядке, возможен бинарный поиск - один из наиболее широко используемых методов поиска. Идея этого метода состоит в том, чтобы искать имя Для получения логарифмического времени поиска существенно устанавливать указатель Бинарный поиск по идее прост, но с деталями условия завершения поиска нужно обращаться осторожно. Частные случаи
Корректность алгоритма 4 следует из утверждения, данного в комментарии в начале тела цикла. Он устанавливает, что если
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.007 с.) |

 в конце таблицы, то цикл всегда будет завершаться отысканием вхождения
в конце таблицы, то цикл всегда будет завершаться отысканием вхождения  . В конце цикла проверка условия
. В конце цикла проверка условия 
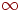 для того, чтобы гарантировать выполнение условия завершения (
для того, чтобы гарантировать выполнение условия завершения (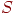 ). Таким образом получаем алгоритм 3.
). Таким образом получаем алгоритм 3.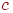 , не зависящее от
, не зависящее от  , последовательно свести задачу поиска в таблице, содержащей
, последовательно свести задачу поиска в таблице, содержащей  за время, не зависящее от
за время, не зависящее от  из
из 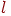 (для "низа") и
(для "низа") и  (для "верха"). Новый указатель
(для "верха"). Новый указатель  (для "средней точки") устанавливается где-то около середины интервала, и либо
(для "средней точки") устанавливается где-то около середины интервала, и либо  или
или  . Если интервал становится пустым, поиск завершается безуспешно.
. Если интервал становится пустым, поиск завершается безуспешно. и
и 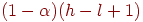 для фиксированного значения
для фиксированного значения  , отличного от
, отличного от  . Когда таблица размещена не последовательно, а хранится в виде списка древовидной структуры, доля
. Когда таблица размещена не последовательно, а хранится в виде списка древовидной структуры, доля  и
и  требуют пристального внимания в любой программе бинарного поиска. В алгоритме 13.4 эти случаи обрабатываются тем же кодом, что и в общем случае, и поучительно посмотреть, как это делается, проследив за выполнением алгоритма для
требуют пристального внимания в любой программе бинарного поиска. В алгоритме 13.4 эти случаи обрабатываются тем же кодом, что и в общем случае, и поучительно посмотреть, как это делается, проследив за выполнением алгоритма для  и
и  .
.
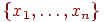 , хранящейся в естественном порядке.
, хранящейся в естественном порядке. ; иначе говоря, при нашем предположении, что имя появляется в таблице не больше одного раза, утверждается, что
; иначе говоря, при нашем предположении, что имя появляется в таблице не больше одного раза, утверждается, что 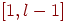 , ни в интервале
, ни в интервале  . Это утверждение очевидно первый раз, когда мы входим в цикл при
. Это утверждение очевидно первый раз, когда мы входим в цикл при  и
и  , и непосредственно по индукции проверяется, что оно выполняется при каждом проходе через цикл. Когда мы выходим из цикла, то должно быть
, и непосредственно по индукции проверяется, что оно выполняется при каждом проходе через цикл. Когда мы выходим из цикла, то должно быть  , и поэтому утверждение принимает вид
, и поэтому утверждение принимает вид  и
и  , откуда следует, что
, откуда следует, что  .
.


