

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Цифровая распределяющая сортировка
Цифровая распределяющая сортировка основана на наблюдении, что если имена уже отсортированы по младшим разрядами  , то их можно полностью отсортировать, сортируя только по старшим разрядам , то их можно полностью отсортировать, сортируя только по старшим разрядам  при условии, что сортировка осуществляется таким образом, чтобы не нарушить относительный порядок имен с одинаковыми цифрами в старших разрядах. при условии, что сортировка осуществляется таким образом, чтобы не нарушить относительный порядок имен с одинаковыми цифрами в старших разрядах.
Эйлеров путь
Эйлеровым путем в графе называется произвольный путь, проходящий через каждое ребро графа в точности один раз.
Раздел 3
Краткие тезисы лекций
Лекция № 1
Основные понятия теории графов. Представление графов. Связность и расстояние графов.
Граф – это конечное множество вершин и ребер, соединяющих их, т. е.:
G = < V,E >,
где V – конечное непустое множество вершин; Е – множество ребер (пар вершин).
Если пары Е (ребра) имеют направление, то граф называется ориентированным (орграф), если иначе - неориентированный (неорграф). Если в пары Е входят только различные вершины, то в графе нет петель. Если ребро графа имеет вес, то граф называется взвешенным. Степень вершины графа равна числу ребер, входящих и выходящих из нее (инцидентных ей). Неорграф называется связным, если существует путь из каждой вершины в любую другую.
Обозначим количество вершин как n = ¦ V ¦, а количество ребер как m = ¦ E ¦.
Представления
Наиболее известный способ представления графа на бумаге состоит в геометрическом изображении точек и линий. В ЭВМ граф должен быть представлен дискретным способом, причем возможно много различных представлений. Простота использования, так же как и эффективность алгоритмов на графе, зависит от подходящего выбора представления графа. Рассмотрим различные структуры данных для представления графов.
Матрица смежностей. Одним из наиболее распространенных машинных представлений простого графа является матрица смежностей или соединений. Матрица смежностей графа 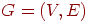 есть есть 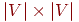 -матрица -матрица 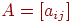 , в которой , в которой 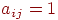 , если в , если в  существует ребро, идущее из существует ребро, идущее из  -й вершины в -й вершины в  -ю, и -ю, и  в противном случае. Орграф и его матрица смежностей представлены на рис. 1. в противном случае. Орграф и его матрица смежностей представлены на рис. 1.

Рис. 1. Ориентированный граф и его матрица смежностей
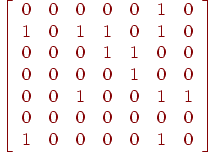
Заметим, что в матрице смежностей петля может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1, но это не принято, так как обычно удобно представлять каждый элемент матрицы одним двоичным разрядом.
Для задания матрицы смежностей требуется 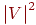 двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и для ее представления достаточно хранить только верхний треугольник. В результате экономится почти 50% памяти, но время вычислений может при этом немного увеличиться, потому что каждое обращение к двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и для ее представления достаточно хранить только верхний треугольник. В результате экономится почти 50% памяти, но время вычислений может при этом немного увеличиться, потому что каждое обращение к 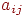 должно быть заменено следующим: if должно быть заменено следующим: if  then then  else else 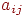 . В случае представления графа его матрицей смежностей для большинства алгоритмов требуется время вычисления, по крайней мере пропорциональное . В случае представления графа его матрицей смежностей для большинства алгоритмов требуется время вычисления, по крайней мере пропорциональное 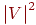 . .
Матрица весов. Граф, в котором ребру  сопоставлено число сопоставлено число  , называется взвешенным графом, а число , называется взвешенным графом, а число  называется весом ребра называется весом ребра  . В сетях связи или транспортных сетях эти веса представляют некоторые физические величины, такие как стоимость, расстояние, эффективность, емкость или надежность соответствующего ребра. Простой взвешенный граф может быть представлен своей матрицей весов . В сетях связи или транспортных сетях эти веса представляют некоторые физические величины, такие как стоимость, расстояние, эффективность, емкость или надежность соответствующего ребра. Простой взвешенный граф может быть представлен своей матрицей весов  , где , где  есть вес ребра, соединяющего вершины есть вес ребра, соединяющего вершины  и и  . Веса несуществующих ребер обычно полагают равными . Веса несуществующих ребер обычно полагают равными 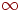 или 0 в зависимости от приложений. Когда вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей. или 0 в зависимости от приложений. Когда вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей.
Список ребер. Если граф является разреженным, то возможно, что более эффектно представлять ребра графа парами вершин. Это представление можно реализовать двумя массивами 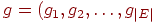 и и 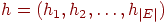 . Каждый элемент в массиве есть метка вершины, а . Каждый элемент в массиве есть метка вершины, а  -е ребро графа выходит из вершины -е ребро графа выходит из вершины 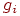 и входит в вершину и входит в вершину  . Например, орграф, изображенный на рис. 1, будет представляться следующим образом: . Например, орграф, изображенный на рис. 1, будет представляться следующим образом:
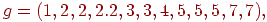
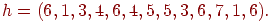
Ясно, что при этом легко представимы петли и кратные ребра.
Структура смежности. В ориентированном графе вершина 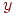 называется последователем другой вершины называется последователем другой вершины  , если существует ребро, направленное из , если существует ребро, направленное из  в в 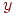 . Вершина . Вершина  называется тогда предшественником называется тогда предшественником 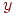 . В случае неориентированного графа две вершины называются соседями, если между ними есть ребро. Граф может быть описан его структурой смежности, то есть списком всех последователей (соседей) каждой вершины; для каждой вершины . В случае неориентированного графа две вершины называются соседями, если между ними есть ребро. Граф может быть описан его структурой смежности, то есть списком всех последователей (соседей) каждой вершины; для каждой вершины  задается задается 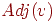 - список всех последователей (соседей) вершины - список всех последователей (соседей) вершины  . В большинстве алгоритмов на графах относительный порядок вершин, смежных с вершиной . В большинстве алгоритмов на графах относительный порядок вершин, смежных с вершиной  в в 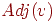 , не важен, и в таком случае удобно считать , не важен, и в таком случае удобно считать 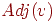 мультимножеством (или множеством, если граф является простым) вершин, смежных с мультимножеством (или множеством, если граф является простым) вершин, смежных с  . Структура смежности орграфа, представленного на рис. 1, такова: . Структура смежности орграфа, представленного на рис. 1, такова:
Adj(v)1: 62: 1, 3, 4, 63: 4, 54: 55: 3, 6, 76:7: 1, 6 Если для хранения метки вершины используется одно машинное слово, то структура смежности ориентированного графа требует  слов. Если граф неориентированный, нужно слов. Если граф неориентированный, нужно  слов, так как каждое ребро встречается дважды. слов, так как каждое ребро встречается дважды.
Структуры смежности могут быть удобно реализованы массивом из  линейно связанных списков, где каждый список содержит последователей некоторой вершины. Поле данных содержит метку одного из последователей, и поле указателей указывает следующего последователя. Хранение списков смежности в виде связанного списка желательно для алгоритмов, в которых в графе добавляются или удаляются вершины. линейно связанных списков, где каждый список содержит последователей некоторой вершины. Поле данных содержит метку одного из последователей, и поле указателей указывает следующего последователя. Хранение списков смежности в виде связанного списка желательно для алгоритмов, в которых в графе добавляются или удаляются вершины.
Матрица инцидентности - 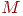 задает граф: задает граф:  если ребро если ребро  выходит из вершины выходит из вершины  , ,  , если ребро , если ребро  входит в вершину входит в вершину  , и , и  в остальных случаях. в остальных случаях.
Связность и расстояние
Говорят, что вершины  и и 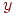 в графе смежны, если существует ребро, соединяющее их. Говорят, что два ребра смежны, если они имеют общую вершину. Простой путь, или для краткости, просто путь, записываемый иногда как в графе смежны, если существует ребро, соединяющее их. Говорят, что два ребра смежны, если они имеют общую вершину. Простой путь, или для краткости, просто путь, записываемый иногда как 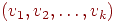 , - это последовательность смежных ребер , - это последовательность смежных ребер 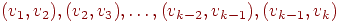 , в которой все вершины , в которой все вершины 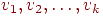 различны, исключая, возможно, случай различны, исключая, возможно, случай 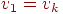 . В орграфе этот путь называется ориентированным из . В орграфе этот путь называется ориентированным из  в в 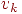 , в неориентированном графе он называется путем между , в неориентированном графе он называется путем между  и и 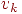 . Число ребер в пути называется длиной пути. Путь наименьшей длины называется кратчайшим путем. Замкнутый путь называется циклом. Граф, который не содержит циклов, называется ациклическим. . Число ребер в пути называется длиной пути. Путь наименьшей длины называется кратчайшим путем. Замкнутый путь называется циклом. Граф, который не содержит циклов, называется ациклическим.
Подграф графа 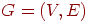 есть граф, вершины и ребра которого лежат в есть граф, вершины и ребра которого лежат в  . Подграф . Подграф  , индуцированный подмножеством , индуцированный подмножеством 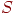 множества множества 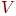 вершин графа вершин графа  , - это подграф, который получается в результате удаления всех вершин из , - это подграф, который получается в результате удаления всех вершин из  и всех ребер, инцидентных им. и всех ребер, инцидентных им.
Неориентированный граф  связен, если существует хотя бы один путь в связен, если существует хотя бы один путь в  между каждой парой вершин между каждой парой вершин  и и  . Ориентированный граф . Ориентированный граф  связен, если неориентированный граф, получающийся из связен, если неориентированный граф, получающийся из  путем удаления ориентации ребер, является связным. Граф, состоящий из единственной изолированной вершины, является (тривиально) связным. Максимальный связный подграф графа путем удаления ориентации ребер, является связным. Граф, состоящий из единственной изолированной вершины, является (тривиально) связным. Максимальный связный подграф графа  называется связной компонентой или просто компонентой называется связной компонентой или просто компонентой  . Несвязный граф состоит из двух или более компонент. Максимальный сильно связный подграф называется сильно связной компонентой. . Несвязный граф состоит из двух или более компонент. Максимальный сильно связный подграф называется сильно связной компонентой.
Иногда недостаточно знать, что граф связен; нас может интересовать, насколько "сильно связен" связный граф. Например, связный граф может содержать вершину, удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся вершины. Такая вершина называется точкой сочленения или разделяющей вершиной. Граф, содержащий точку сочленения, называется разделимым. Граф без точек сочленения называется двусвязным или неразделимым. Максимальный двусвязный подграф графа называется двусвязной компонентой или блоком.
Большинство основных вопросов о графах касается связности, путей и расстояний. Нас может интересовать вопрос, является ли граф связным; если он связен, то может оказаться нужным найти кратчайшее расстояние между выделенной парой вершин или определить кратчайший путь между ними. Если граф несвязен, то может потребоваться найти все его компоненты. В нашем курсе строятся алгоритмы для решения этих и других подобных вопросов.
Лекция № 2
Остовные деревья. Клики. Изоморфизм. Планарность.
Остовные деревья
Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом. В связном неориентированном графе  существует по крайней мере один путь между каждой парой вершин; отсутствие циклов в существует по крайней мере один путь между каждой парой вершин; отсутствие циклов в  означает, что существует самое большее один такой путь между любой парой вершин в означает, что существует самое большее один такой путь между любой парой вершин в  . Поэтому, если . Поэтому, если  - дерево, то между каждой парой вершин в - дерево, то между каждой парой вершин в  существует в точности один путь. Рассуждение легко обратимо, и поэтому неориентированный граф существует в точности один путь. Рассуждение легко обратимо, и поэтому неориентированный граф  будет деревом тогда и только тогда, если между каждой парой вершин в будет деревом тогда и только тогда, если между каждой парой вершин в  существует в точности один путь. Так как наименьшее число ребер, которыми можно соединить существует в точности один путь. Так как наименьшее число ребер, которыми можно соединить  вершин, равно вершин, равно  и дерево с и дерево с  вершинами содержит в точности вершинами содержит в точности  ребер, то деревья можно считать минимально связными графами. Удаление из дерева любого ребра превращает его в несвязный граф, разрушая единственный путь между по крайней мере одной парой вершин. ребер, то деревья можно считать минимально связными графами. Удаление из дерева любого ребра превращает его в несвязный граф, разрушая единственный путь между по крайней мере одной парой вершин.
Особый интерес представляют остовные деревья графа  , то есть деревья, являющиеся подграфами графа , то есть деревья, являющиеся подграфами графа  и содержащие все его вершины. Если граф и содержащие все его вершины. Если граф  несвязен, то множество, состоящее из остовных деревьев каждой компоненты называется остовном лесом графа. Для построения остовного дерева (леса) данного неориентированного графа несвязен, то множество, состоящее из остовных деревьев каждой компоненты называется остовном лесом графа. Для построения остовного дерева (леса) данного неориентированного графа  , мы последовательно просматриваем ребра , мы последовательно просматриваем ребра  , оставляя те, которые не образуют циклов с уже выбранными. , оставляя те, которые не образуют циклов с уже выбранными.
Во взвешенном графе 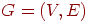 часто интересно определить остовное дерево (лес) с минимальным общим весом ребер, то есть дерево (лес), у которого сумма весов всех его ребер минимальна. Такое дерево называется минимумом оставных деревьев или минимальное остовное дерево. Другими словами, на каждом шаге мы выбираем новое ребро с наименьшим весом (наименьшее ребро), не образующее циклов с уже выбранными ребрами; этот процесс продолжаем до тех пор, пока не будет выбрано часто интересно определить остовное дерево (лес) с минимальным общим весом ребер, то есть дерево (лес), у которого сумма весов всех его ребер минимальна. Такое дерево называется минимумом оставных деревьев или минимальное остовное дерево. Другими словами, на каждом шаге мы выбираем новое ребро с наименьшим весом (наименьшее ребро), не образующее циклов с уже выбранными ребрами; этот процесс продолжаем до тех пор, пока не будет выбрано 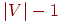 ребер, образующих остовное дерево ребер, образующих остовное дерево  . Этот процесс известен как жадный алгоритм. . Этот процесс известен как жадный алгоритм.
Жадный алгоритм может быть выполнен в два этапа. Сначала ребра сортируются по весу и затем строится остовное дерево путем выбора наименьших из имеющихся в распоряжении ребер.
Существует другой метод получения минимума остовных деревьев, который не требует ни сортировки ребер, ни проверки на цикличность на каждом шаге, - так называемый алгоритм ближайшего соседа. Мы начинаем с некоторой произвольной вершины  в заданном графе. Пусть в заданном графе. Пусть  - ребро с наименьшим весом, инцидентное - ребро с наименьшим весом, инцидентное  ; ребро ; ребро  включается в дерево. Затем среди всех ребер, инцидентных либо включается в дерево. Затем среди всех ребер, инцидентных либо  , либо , либо  , выбираем ребро с наименьшим весом и включаем его в частично построенное дерево. В результате этого в дерево добавляется новая вершина, например, , выбираем ребро с наименьшим весом и включаем его в частично построенное дерево. В результате этого в дерево добавляется новая вершина, например, 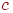 . Повторяя процесс, ищем наименьшее ребро, соединяющее . Повторяя процесс, ищем наименьшее ребро, соединяющее  , ,  или или 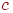 с некоторой другой вершиной графа. Процесс продолжается до тех пор, пока все вершины из с некоторой другой вершиной графа. Процесс продолжается до тех пор, пока все вершины из  не будут включены в дерево, то есть пока дерево не станет остовным. не будут включены в дерево, то есть пока дерево не станет остовным.
Наихудшим для этого алгоритма будет случай, когда  - полный граф (то есть когда каждая пара вершин в графе соединена ребром); в этом случае для того, чтобы найти ближайшего соседа, на каждом шаге нужно сделать максимальное число сравнений. Чтобы выбрать первое ребро, мы сравниваем веса всех - полный граф (то есть когда каждая пара вершин в графе соединена ребром); в этом случае для того, чтобы найти ближайшего соседа, на каждом шаге нужно сделать максимальное число сравнений. Чтобы выбрать первое ребро, мы сравниваем веса всех 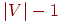 ребер, инцидентных вершине ребер, инцидентных вершине  , и выбираем наименьшее; этот шаг требует , и выбираем наименьшее; этот шаг требует  сравнений. Для выбора второго ребра мы ищем наименьшее среди возможных сравнений. Для выбора второго ребра мы ищем наименьшее среди возможных 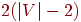 ребер (инцидентных ребер (инцидентных  или или  ) и делаем для этого ) и делаем для этого  сравнений. Таким образом, ясно, что для выбора сравнений. Таким образом, ясно, что для выбора  -го ребра требуется -го ребра требуется  сравнений, и поэтому в сумме потребуется сравнений, и поэтому в сумме потребуется
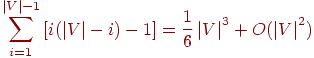
сравнений для построения минимума остовных деревьев.
Клики
Максимальный полный подграф графа  называется кликой графа называется кликой графа  ; другими словами, клика графа ; другими словами, клика графа  есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством. Например, на рис. 2 показан граф и его клики. есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством. Например, на рис. 2 показан граф и его клики.
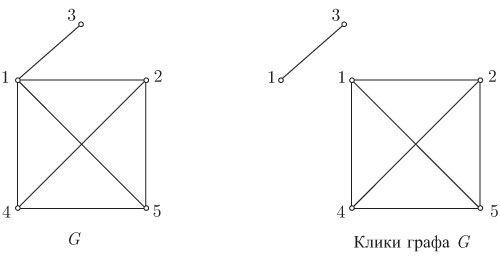
Рис. 2. Граф G и все его клики
Клики графа представляют "естественные" группировки вершин, и определение клик графа полезно в кластерном анализе в таких областях, как информационный поиск и социология.
Изоморфизм
Два графа  называются изоморфными, если существует взаимно однозначное соответствие называются изоморфными, если существует взаимно однозначное соответствие  , такое, что , такое, что  тогда и только тогда, если тогда и только тогда, если  , то есть существует соответствие между вершинами графа , то есть существует соответствие между вершинами графа 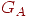 и вершинами графа и вершинами графа  , сохраняющее отношение смежности. Например, на рис. 2 показаны два изоморфных орграфа: вершины , сохраняющее отношение смежности. Например, на рис. 2 показаны два изоморфных орграфа: вершины 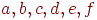 в орграфе в орграфе  соответствуют вершинам 2, 3, 6, 1, 4, 5 в указанном порядке в орграфе соответствуют вершинам 2, 3, 6, 1, 4, 5 в указанном порядке в орграфе 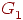 . Вообще говоря, между . Вообще говоря, между 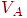 и и 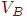 может быть более чем одно соответствие, и на рис. 3 графы имеют на самом деле второй изоморфизм: может быть более чем одно соответствие, и на рис. 3 графы имеют на самом деле второй изоморфизм: 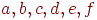 соответствуют в указанном порядке вершинам 2, 3, 6, 1, 5, 4. Изоморфные графы отличаются только метками вершин, в связи с чем задача определения изоморфизма возникает в ряде практических ситуаций, таких, как информационный поиск и определение химических соединений. соответствуют в указанном порядке вершинам 2, 3, 6, 1, 5, 4. Изоморфные графы отличаются только метками вершин, в связи с чем задача определения изоморфизма возникает в ряде практических ситуаций, таких, как информационный поиск и определение химических соединений.
Заметим, что можно ограничится орграфами. Любой неориентированный граф превращается в орграф заменой каждого ребра двумя противоположно направленными ребрами. Два полученные таким образом орграфа, очевидно, изоморфны тогда и только тогда, если изоморфны исходные графы.
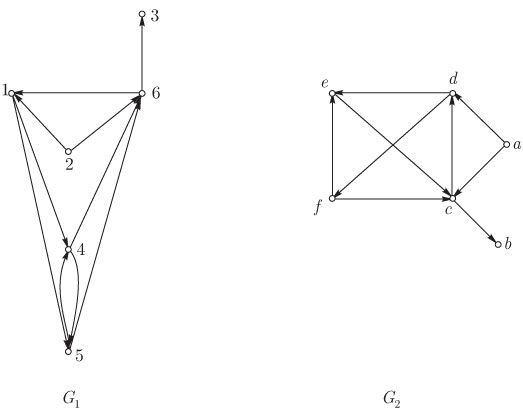
Рис. 3. Изоморфные орграфы
Планарность
Граф называют планарным, если существует такое изображение на плоскости его вершин и ребер, что:
- каждая вершина
 изображается отдельной точкой изображается отдельной точкой  на плоскости; на плоскости; - каждое ребро
 изображается простой кривой, имеющей концевые точки изображается простой кривой, имеющей концевые точки  ; ; - эти кривые пересекаются только в общих концевых точках. Задача определения того, можно ли изобразить граф на плоскости без пересечения ребер, имеет большой практический интерес (например, при конструировании интегральных схем или печатных плат необходимо выяснить, можно ли окончательную схему вложить в плоскость).
Определение планарности графа отличается от других рассмотренных нами задач, поскольку при изображении точек и линий на плоскости приходится больше иметь дело с непрерывными, а не с дискретными величинами. Взаимосвязь между дискретными и непрерывными аспектами планарности заинтересовала математиков и привела к различным характеристикам планарных графов. С точки зрения математики эти характеристики изящны, но эффективных алгоритмов определения планарности они не дают. Наиболее успешный подход к определению планарности состоит просто в том, что граф разбивается на подграфы и затем делается попытка разместить его на плоскости, добавляя подграфы один за другим и сохраняя при размещении планарность.
Вначале сделаем несколько простых, но полезных наблюдений. Поскольку орграф планарен тогда и только тогда, если планарен соответствующий неориентированный граф, полученный игнорированием направления ребер, то достаточно рассматривать только неориентированные графы, поскольку неориентированный граф планарен тогда и только тогда, если все его двусвязные компоненты планарны. Поэтому если неориентированный граф является разделимым, мы можем разложить его на двусвязные компоненты и рассматривать их отдельно. Наконец, поскольку параллельные ребра и петли всегда можно добавить к графу или удалить из него без нарушения свойства планарности, нам достаточно рассматривать только простые графы. Поэтому при определении планарности будем предполагать, что граф неориентированный, простой и двусвязный.
Наша основная стратегия состоит прежде всего в том, чтобы в графе  найти цикл найти цикл  , разместить , разместить  на плоскости в виде простой замкнутой кривой, разложить оставшуюся часть на плоскости в виде простой замкнутой кривой, разложить оставшуюся часть 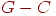 на непересекающиеся по ребрам пути и затем попытаться разместить каждый из этих путей либо целиком внутри на непересекающиеся по ребрам пути и затем попытаться разместить каждый из этих путей либо целиком внутри  , либо целиком вне , либо целиком вне  . Если нам удалось разместить так весь граф . Если нам удалось разместить так весь граф  , то он планарен, в противном случае он непланарен. Трудность этого способа заключается в том, что при размещении путей можно выбирать либо внутренность, либо внешность , то он планарен, в противном случае он непланарен. Трудность этого способа заключается в том, что при размещении путей можно выбирать либо внутренность, либо внешность  , и мы должны проконтролировать, чтобы неправильный выбор области размещения на ранней стадии не устранял возможности размещения последующих путей, - это могло бы привести нас к неверному заключению, что планарный граф непланарен. , и мы должны проконтролировать, чтобы неправильный выбор области размещения на ранней стадии не устранял возможности размещения последующих путей, - это могло бы привести нас к неверному заключению, что планарный граф непланарен.
Лекция № 3
Задача поиска. Поиск и другие операции над таблицами. Последовательный поиск.
Задача поиска является фундаментальной в комбинаторных алгоритмах, так как она формулируется в такой общности, что включает в себя множество задач, представляющих практический интерес. При самой общей постановке "Исследовать множество  с тем чтобы найти элемент, удовлетворяющий некоторому условию с тем чтобы найти элемент, удовлетворяющий некоторому условию  ", о задаче поиска едва ли можно сказать что-либо стоящее. Удивительно, однако, что достаточно незначительных ограничений на структуру множества ", о задаче поиска едва ли можно сказать что-либо стоящее. Удивительно, однако, что достаточно незначительных ограничений на структуру множества  , чтобы задача стала интересной: возникает множество разнообразных стратегий поиска различной степени эффективности. Мы сделаем некоторые предположения о структуре множества , чтобы задача стала интересной: возникает множество разнообразных стратегий поиска различной степени эффективности. Мы сделаем некоторые предположения о структуре множества  , позволяющие исследовать , позволяющие исследовать   или или  . Большинство алгоритмов поиска попадает в одну из трех категорий, характеризуемых временем поиска . Большинство алгоритмов поиска попадает в одну из трех категорий, характеризуемых временем поиска  . .
Поиск и другие операции над таблицами
Любой способ поиска оперирует с элементами, которые будем называть именами, взятыми из множества имен 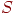 - оно называется пространством имен. Это пространство имен может быть конечным или бесконечным. Самыми распространенными пространствами имен являются множества целых чисел с их числовым порядком (нумерацией), и множества последовательностей символов над некоторым конечным алфавитом с их лексикографическим (то есть словарным) порядком. Каждый из алгоритмов поиска, обсуждаемых в этой лекции, основан на одном из трех следующих предположений о пространстве - оно называется пространством имен. Это пространство имен может быть конечным или бесконечным. Самыми распространенными пространствами имен являются множества целых чисел с их числовым порядком (нумерацией), и множества последовательностей символов над некоторым конечным алфавитом с их лексикографическим (то есть словарным) порядком. Каждый из алгоритмов поиска, обсуждаемых в этой лекции, основан на одном из трех следующих предположений о пространстве 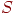 . .
Предположение 1. На 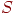 определен линейный порядок, называемый естественным порядком и обозначаемый знаком <. Такой порядок имеет следующие свойства. определен линейный порядок, называемый естественным порядком и обозначаемый знаком <. Такой порядок имеет следующие свойства.
1. Любые два элемента 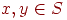 сравнимы, то есть должно выполняться в точности одно из трех условий: сравнимы, то есть должно выполняться в точности одно из трех условий:  , , 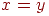 , ,  . .
2. Порядок обладает транзитивностью, то есть если  и и 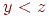 , то , то  для любых элементов для любых элементов 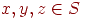 . Мы используем обозначения . Мы используем обозначения  , ,  , ,  в очевидном смысле. При анализе эффективности алгоритма поиска полагаем, что исход ( в очевидном смысле. При анализе эффективности алгоритма поиска полагаем, что исход ( , ,  или или  ) зависит от сравнения. ) зависит от сравнения.
Предположение 2. Каждое имя в 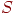 есть последовательность символов или цифр над конечным линейно упорядоченным алфавитом есть последовательность символов или цифр над конечным линейно упорядоченным алфавитом  . Естественным порядком на . Естественным порядком на 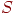 является лексикографический порядок, индуцированный линейным порядком на является лексикографический порядок, индуцированный линейным порядком на  . Мы полагаем, что исход ( . Мы полагаем, что исход ( , ,  или или  ) сравнения двух символов (не имен) получается за время, не зависящее от ) сравнения двух символов (не имен) получается за время, не зависящее от  или или  . .
Предположение 3. Имеется функция 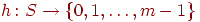 , которая равномерно отображает пространство имен , которая равномерно отображает пространство имен 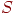 в множество в множество 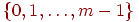 , то есть все целые , то есть все целые  , приблизительно с одинаковой частотой являются образами имен из , приблизительно с одинаковой частотой являются образами имен из 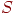 при отображении при отображении  . Мы полагаем, что функция . Мы полагаем, что функция  не зависела от не зависела от  , это с теоретической точки зрения выглядит шатко, но с практической - довольно реально. , это с теоретической точки зрения выглядит шатко, но с практической - довольно реально.
Как уже было отмечено, поиск производится не в самом пространстве 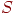 имен, а в конечном подмножестве имен, а в конечном подмножестве 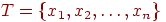 множества множества 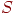 , называемом таблицей. На большинстве таблиц, которые мы рассматриваем, определен линейный порядок, называемый табличным порядком: ему соответствует нижний индекс имени (то есть , называемом таблицей. На большинстве таблиц, которые мы рассматриваем, определен линейный порядок, называемый табличным порядком: ему соответствует нижний индекс имени (то есть  есть первое имя в таблице, есть первое имя в таблице,  - второе и тому подобное). Табличный порядок часто совпадает с естественным порядком, определенным на пространстве имен, однако такое совпадение не обязательно. - второе и тому подобное). Табличный порядок часто совпадает с естественным порядком, определенным на пространстве имен, однако такое совпадение не обязательно.
Мощность таблицы  обычно намного меньше, чем мощность пространства имен обычно намного меньше, чем мощность пространства имен 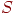 , даже если , даже если 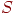 конечно. конечно.
Представление о таблице как об упорядоченном множестве имен существенно для многих целей. Но иногда бывает необходимо рассматривать таблицу как множество ячеек, каждая из которых может содержать одно имя. Например, если процесс включения нового имени рассматривать более подробно, то обнаружится, что сначала нужно расширить таблицу добавлением ячейки, для того чтобы заготовить место для новой записи: только потом туда заносится новое имя.
Мы будем предполагать, что имена появляются в таблице не больше одного раза (исключение составляет переходный период, в течение которого заносится новое имя; в таблице допускается два вхождения одного имени). В большинстве случаев вследствие такого предположения таблица с  именами имеет ровно именами имеет ровно  ячеек. Однако важный класс алгоритмов, основанных на вычислении адреса, опирается на предположение о том, что таблица содержит больше ячеек, чем имен. Эти алгоритмы должны четко принимать во внимание наличие пустых ячеек. ячеек. Однако важный класс алгоритмов, основанных на вычислении адреса, опирается на предположение о том, что таблица содержит больше ячеек, чем имен. Эти алгоритмы должны четко принимать во внимание наличие пустых ячеек.
Существует ряд синонимов для объектов, именуемых здесь таблицей и именем. В обработке данных существуют файлы, элементами которых являются записи; каждая запись есть последовательность полей, одно из которых (участвующее в поиске) называется ключом. Если сам файл проходится во время поиска, "файл" и "ключ" представляют собой то, что мы называем "таблицей" и "именем" соответственно. (Эта терминология несколько двусмысленна, поскольку понятие "ключ" можно отнести либо к самой ячейке, либо к содержимому ячейки.) Однако при поиске в большом файле часто не подразумевается просмотр самого файла; вместо этого поиск осуществляется на справочнике или указателе файла. При успешном поиске найденная в указателе отдельная запись указывает на соответствующую запись в файле. В таком типе организации файлов нашему понятию таблицы соответствует указатель или справочник.
Мы рассматриваем только четыре табличные операции: поиск, включение, исключение и распечатка. Подробное определение того, что должны делать эти операции над таблицей 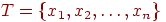 , зависит от структуры данных, использованной для реализации таблицы. , зависит от структуры данных, использованной для реализации таблицы.
поиск  : если : если  , то отметить его указателем, то есть переменной , то отметить его указателем, то есть переменной  присвоить такое значение, что присвоить такое значение, что 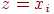 ; в противном случае указать, что ; в противном случае указать, что 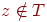 ; ;
включение  : если : если 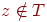 , то поместить его на соответствующее место. , то поместить его на соответствующее место.
Включение в общем случае предполагает прежде всего поиск соответствующего места, поэтому иногда удобно разделить операцию на две фазы. Сначала используем процедуру поиска для отыскания места, куда должно быть помещено  , и затем помещаем z на это место. , и затем помещаем z на это место.
включить  на на  -е место: включить -е место: включить  сразу после имени сразу после имени  . До включения . До включения 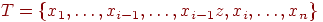 . .
исключить  : если : если  , то исключить его. , то исключить его.
Как и включение, исключение иногда реализуется процедурой поиска для получения места  и последующей процедурой: и последующей процедурой:
исключить с  -го места: исключить -го места: исключить 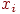 из из  .До исключения .До исключения 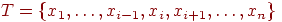 \\ & После исключения \\ & После исключения 
Таблица, в которой осуществляются включения или исключения, называется динамической; в противном случае она носит название статической.
Последней операцией, которую мы будем рассматривать для каждой табличной структуры, является
распечатка: & напечатать все имена из  в их естественном порядке в их естественном порядке
Среди всех операций, которые можно производить над таблицами, четыре, рассматриваемые в этой лекции (поиск, включение, исключение и распечатка), и сортировка - наиболее важные.
Последовательный поиск
Под последовательным поиском мы подразумеваем исследование имен в том порядке, в котором они встречаются в таблице. При таком поиске в таблице в худшем случае получается просмотр всей таблицы; даже в среднем последовательный поиск имеет тенденцию к использованию числа операций, пропорционального  . Для больших таблиц его не следует относить к методам быстрого поиска, поскольку последовательный поиск асимптотически гораздо медленнее других алгоритмов, описанных в этой лекции. Несмотря на его низкие асимптотические возможности, имеется ряд причин, по которым этот метод следует обсудить вначале. Во-первых, хотя идея его проста, он позволяет нам ввести важные понятия и методы, применимые к поиску вообще. Во-вторых, последовательный поиск является единственным методом поиска, применимым к отдельным устройствам памяти и к тем таблицам, которые строятся на пространстве имен без линейного порядка. Наконец, последовательный поиск является быстрым для достаточно малых таблиц и для больших таблиц, организованных иерархическим способом: более быстрый метод используется для исследования окрестности верхушки иерархии, а последовательный поиск – для подтаблицы на нижнем уровне иерархии. . Для больших таблиц его не следует относить к методам быстрого поиска, поскольку последовательный поиск асимптотически гораздо медленнее других алгоритмов, описанных в этой лекции. Несмотря на его низкие асимптотические возможности, имеется ряд причин, по которым этот метод следует обсудить вначале. Во-первых, хотя идея его проста, он позволяет нам ввести важные понятия и методы, применимые к поиску вообще. Во-вторых, последовательный поиск является единственным методом поиска, применимым к отдельным устройствам памяти и к тем таблицам, которые строятся на пространстве имен без линейного порядка. Наконец, последовательный поиск является быстрым для достаточно малых таблиц и для больших таблиц, организованных иерархическим способом: более быстрый метод используется для исследования окрестности верхушки иерархии, а последовательный поиск – для подтаблицы на нижнем уровне иерархии.
Для последовательного поиска по таблице 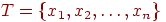 мы предполагаем, что имеется указатель мы предполагаем, что имеется указатель  , значение которого принадлежит отрезку , значение которого принадлежит отрезку  или, возможно, или, возможно,  . Над этим указателем разрешается производить только следующие операции; первоначальное присваивание ему значения 1 или . Над этим указателем разрешается производить только следующие операции; первоначальное присваивание ему значения 1 или  (или, если удобнее, 0 или (или, если удобнее, 0 или  , увеличение и /или уменьшение его на единицу и сравнение его с 0, 1, , увеличение и /или уменьшение его на единицу и сравнение его с 0, 1,  или или  . При таких соглашениях наиболее очевидный алгоритм поиска в таблице . При таких соглашениях наиболее очевидный алгоритм поиска в таблице  первого вхождения данного имени первого вхождения данного имени  имеет вид алгоритма 13.1. Здесь, как и во всех других алгоритмах поиска, изложенных в настоящей лекции, мы полагаем, что алгоритм останавливается немедленно по отыскании имеет вид алгоритма 13.1. Здесь, как и во всех других алгоритмах поиска, изложенных в настоящей лекции, мы полагаем, что алгоритм останавливается немедленно по отыскании 
| Поделиться:
| |



 , то их можно полностью отсортировать, сортируя только по старшим разрядам
, то их можно полностью отсортировать, сортируя только по старшим разрядам  при условии, что сортировка осуществляется таким образом, чтобы не нарушить относительный порядок имен с одинаковыми цифрами в старших разрядах.
при условии, что сортировка осуществляется таким образом, чтобы не нарушить относительный порядок имен с одинаковыми цифрами в старших разрядах.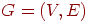 есть
есть 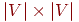 -матрица
-матрица 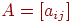 , в которой
, в которой 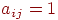 , если в
, если в  существует ребро, идущее из
существует ребро, идущее из  -й вершины в
-й вершины в  -ю, и
-ю, и  в противном случае. Орграф и его матрица смежностей представлены на рис. 1.
в противном случае. Орграф и его матрица смежностей представлены на рис. 1.
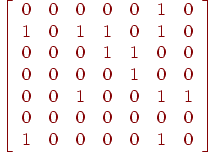
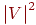 двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и для ее представления достаточно хранить только верхний треугольник. В результате экономится почти 50% памяти, но время вычислений может при этом немного увеличиться, потому что каждое обращение к
двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и для ее представления достаточно хранить только верхний треугольник. В результате экономится почти 50% памяти, но время вычислений может при этом немного увеличиться, потому что каждое обращение к 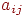 должно быть заменено следующим: if
должно быть заменено следующим: if  then
then  else
else  сопоставлено число
сопоставлено число  , называется взвешенным графом, а число
, называется взвешенным графом, а число  , где
, где 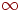 или 0 в зависимости от приложений. Когда вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей.
или 0 в зависимости от приложений. Когда вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей.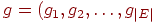 и
и 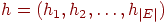 . Каждый элемент в массиве есть метка вершины, а
. Каждый элемент в массиве есть метка вершины, а 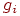 и входит в вершину
и входит в вершину  . Например, орграф, изображенный на рис. 1, будет представляться следующим образом:
. Например, орграф, изображенный на рис. 1, будет представляться следующим образом: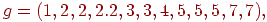
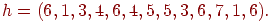
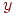 называется последователем другой вершины
называется последователем другой вершины  , если существует ребро, направленное из
, если существует ребро, направленное из  задается
задается 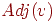 - список всех последователей (соседей) вершины
- список всех последователей (соседей) вершины  слов. Если граф неориентированный, нужно
слов. Если граф неориентированный, нужно  слов, так как каждое ребро встречается дважды.
слов, так как каждое ребро встречается дважды. линейно связанных списков, где каждый список содержит последователей некоторой вершины. Поле данных содержит метку одного из последователей, и поле указателей указывает следующего последователя. Хранение списков смежности в виде связанного списка желательно для алгоритмов, в которых в графе добавляются или удаляются вершины.
линейно связанных списков, где каждый список содержит последователей некоторой вершины. Поле данных содержит метку одного из последователей, и поле указателей указывает следующего последователя. Хранение списков смежности в виде связанного списка желательно для алгоритмов, в которых в графе добавляются или удаляются вершины.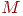 задает граф:
задает граф:  если ребро
если ребро  , если ребро
, если ребро  в остальных случаях.
в остальных случаях.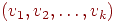 , - это последовательность смежных ребер
, - это последовательность смежных ребер 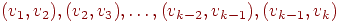 , в которой все вершины
, в которой все вершины 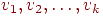 различны, исключая, возможно, случай
различны, исключая, возможно, случай 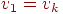 . В орграфе этот путь называется ориентированным из
. В орграфе этот путь называется ориентированным из  в
в 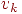 , в неориентированном графе он называется путем между
, в неориентированном графе он называется путем между 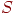 множества
множества 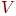 вершин графа
вершин графа  и всех ребер, инцидентных им.
и всех ребер, инцидентных им. и
и  . Ориентированный граф
. Ориентированный граф  вершин, равно
вершин, равно  и дерево с
и дерево с 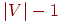 ребер, образующих остовное дерево
ребер, образующих остовное дерево  . Этот процесс известен как жадный алгоритм.
. Этот процесс известен как жадный алгоритм. в заданном графе. Пусть
в заданном графе. Пусть  - ребро с наименьшим весом, инцидентное
- ребро с наименьшим весом, инцидентное  , выбираем ребро с наименьшим весом и включаем его в частично построенное дерево. В результате этого в дерево добавляется новая вершина, например,
, выбираем ребро с наименьшим весом и включаем его в частично построенное дерево. В результате этого в дерево добавляется новая вершина, например, 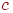 . Повторяя процесс, ищем наименьшее ребро, соединяющее
. Повторяя процесс, ищем наименьшее ребро, соединяющее  сравнений. Для выбора второго ребра мы ищем наименьшее среди возможных
сравнений. Для выбора второго ребра мы ищем наименьшее среди возможных 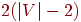 ребер (инцидентных
ребер (инцидентных  сравнений. Таким образом, ясно, что для выбора
сравнений. Таким образом, ясно, что для выбора  сравнений, и поэтому в сумме потребуется
сравнений, и поэтому в сумме потребуется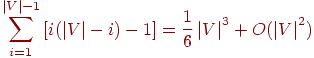

 называются изоморфными, если существует взаимно однозначное соответствие
называются изоморфными, если существует взаимно однозначное соответствие  , такое, что
, такое, что  тогда и только тогда, если
тогда и только тогда, если  , то есть существует соответствие между вершинами графа
, то есть существует соответствие между вершинами графа 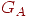 и вершинами графа
и вершинами графа  , сохраняющее отношение смежности. Например, на рис. 2 показаны два изоморфных орграфа: вершины
, сохраняющее отношение смежности. Например, на рис. 2 показаны два изоморфных орграфа: вершины 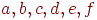 в орграфе
в орграфе  соответствуют вершинам 2, 3, 6, 1, 4, 5 в указанном порядке в орграфе
соответствуют вершинам 2, 3, 6, 1, 4, 5 в указанном порядке в орграфе 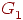 . Вообще говоря, между
. Вообще говоря, между 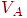 и
и 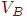 может быть более чем одно соответствие, и на рис. 3 графы имеют на самом деле второй изоморфизм:
может быть более чем одно соответствие, и на рис. 3 графы имеют на самом деле второй изоморфизм: 
 на плоскости;
на плоскости;  изображается простой кривой, имеющей концевые точки
изображается простой кривой, имеющей концевые точки  ;
;  , разместить
, разместить 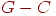 на непересекающиеся по ребрам пути и затем попытаться разместить каждый из этих путей либо целиком внутри
на непересекающиеся по ребрам пути и затем попытаться разместить каждый из этих путей либо целиком внутри  или
или  . Большинство алгоритмов поиска попадает в одну из трех категорий, характеризуемых временем поиска
. Большинство алгоритмов поиска попадает в одну из трех категорий, характеризуемых временем поиска  .
.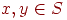 сравнимы, то есть должно выполняться в точности одно из трех условий:
сравнимы, то есть должно выполняться в точности одно из трех условий:  ,
, 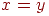 ,
,  .
.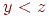 , то
, то  для любых элементов
для любых элементов 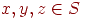 . Мы используем обозначения
. Мы используем обозначения  ,
,  ,
,  в очевидном смысле. При анализе эффективности алгоритма поиска полагаем, что исход (
в очевидном смысле. При анализе эффективности алгоритма поиска полагаем, что исход ( ,
,  или
или  . Естественным порядком на
. Естественным порядком на  . Мы полагаем, что исход (
. Мы полагаем, что исход ( или
или 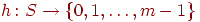 , которая равномерно отображает пространство имен
, которая равномерно отображает пространство имен 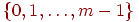 , то есть все целые
, то есть все целые  , приблизительно с одинаковой частотой являются образами имен из
, приблизительно с одинаковой частотой являются образами имен из  . Мы полагаем, что функция
. Мы полагаем, что функция 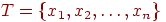 множества
множества  есть первое имя в таблице,
есть первое имя в таблице,  - второе и тому подобное). Табличный порядок часто совпадает с естественным порядком, определенным на пространстве имен, однако такое совпадение не обязательно.
- второе и тому подобное). Табличный порядок часто совпадает с естественным порядком, определенным на пространстве имен, однако такое совпадение не обязательно. : если
: если  , то отметить его указателем, то есть переменной
, то отметить его указателем, то есть переменной 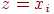 ; в противном случае указать, что
; в противном случае указать, что 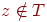 ;
; . До включения
. До включения 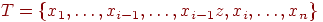 .
.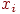 из
из 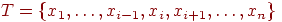 \\ & После исключения
\\ & После исключения 
 или, возможно,
или, возможно,  . Над этим указателем разрешается производить только следующие операции; первоначальное присваивание ему значения 1 или
. Над этим указателем разрешается производить только следующие операции; первоначальное присваивание ему значения 1 или  , увеличение и /или уменьшение его на единицу и сравнение его с 0, 1,
, увеличение и /или уменьшение его на единицу и сравнение его с 0, 1,  . При таких соглашениях наиболее очевидный алгоритм поиска в таблице
. При таких соглашениях наиболее очевидный алгоритм поиска в таблице 


