
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, решаемые методом сортировки. Алгоритмы сортировки.Содержание книги
Поиск на нашем сайте
on_load_lecture() Рассматриваемые здесь задачи можно отнести к наиболее часто встречающимся классам комбинаторных задач. Почти во всех машинных приложениях множество объектов должно быть переразмещено в соответствии с некоторым заранее определенным порядком. Например, при обработке коммерческих данных часто бывает необходимо расположить их по алфавиту или по возрастанию номеров. В числовых расчетах иногда требуется знать наибольший корень многочлена, и т.д. Будем считать заданной таблицу с При внутренней сортировке решается задача полной сортировки для случая достаточно малой таблицы, умещающейся непосредственно в адресной памяти. Внешняя сортировка представляет собой задачу полной сортировки для случая такой большой таблицы, что доступ к ней организован по частям, расположенным на внешних запоминающих устройствах. Частичная сортировка - задачи выбора Внутренняя сортировка Существует по крайней мере пять широких классов алгоритмов внутренней сортировки. 1. Вставка. На
2. Обмен. Два имени, расположение которых не соответствует порядку, меняются местами (обмен). Эти процедуры повторяются до тех пор, пока остаются такие пары.
3. Выбор. На
4. Распределение. Имена распределяются по группам, и содержимое групп затем объединяется таким образом, чтобы частично отсортировать таблицу; процесс повторяется до тех пор, пока таблица не будет отсортирована полностью. 5. Слияние. Таблица делится на подтаблицы, которые сортируются по отдельности и затем сливаются в одну.
Эти классы нельзя назвать ни взаимоисключающими, ни исчерпывающими: одни алгоритмы сортировки можно с полным основанием отнести более чем к одному классу (пузырьковую сортировку можно рассматривать и как выбор, и как обмен), а другие не укладываются ни в один из классов. Тем не менее, перечисленные пять классов достаточно удобны для классификации обсуждаемых алгоритмов сортировки. Сосредоточим внимание на первых четырех классах алгоритмов сортировки. Алгоритмы, основанные на слиянии, приемлемы для внутренней сортировки, но более естественно рассматривать их как методы внешней сортировки. В описываемых алгоритмах сортировки имена образуют последовательность, которую будем обозначать
Таким образом, операция В каждом из рассматриваемых алгоритмов будем считать, что имена нужно сортировать на месте. Другими словами, переразмещение имен должно происходить внутри последовательности Вставка Вставка - простейшая сортировка вставками проходит через этапы
При вставке имя
Эффективность этого алгоритма, как и большинства алгоритмов сортировки, зависит от числа сравнений имен и числа пересылок данных, осуществляемых в трех случаях: худшем, среднем (в предположении, что все on_load_lecture() Обменная сортировка Обменная сортировка некоторым систематическим образом меняет местами пары имен, не отвечающие порядку, до тех пор, пока такие пары существуют. Фактически алгоритм 1 можно рассматривать как обменную сортировку, в которой имя Пузырьковая сортировка. Наиболее очевидный метод систематического обмена местами имен с неправильным порядком состоит в просмотре пар смежных имен последовательно слева направо и перемене мест тех имен, которые не отвечают порядку.
Эта техника получила название пузырьковой сортировки, так как большие имена "пузырьками всплывают" вверх (то есть на правый конец) таблицы. В алгоритме 2 эта простая идея реализуется с одним небольшим усовершенствованием: ясно, что не имеет смысла продолжать просмотр для больших имен (в правом конце таблицы), про которые известно, что они находятся на своих окончательных позициях. В алгоритме 2 используется переменная
Анализ пузырьковой сортировки зависит от трех факторов: числа проходов (то есть числа выполнений тела цикла Пузырьковую сортировку можно несколько улучшить, но при этом она все еще не сможет конкурировать с более эффективными алгоритмами сортировки. Ее единственным преимуществом является простота. Как в простой сортировке вставками, так и в пузырьковой сортировке (алгоритм 2) основной причиной неэффективности является тот факт, что обмены дают слишком малый эффект, так как в каждый момент времени имена сдвигаются только на одну позицию. Такие алгоритмы непременно требуют порядка Быстрая сортировка. Идея метода быстрой сортировки состоит в том, чтобы выбрать одно из имен в таблице и использовать его для разделения таблицы на две подтаблицы, составленные соответственно из имен меньших и больших выбранного, которые затем рекурсивно сортируются с использованием быстрой сортировки. Разделение можно реализовать, одновременно просматривая таблицу и слева направо, и справа налево, меняя местами имена в неправильных частях таблицы. Имя, используемое для расщепления таблицы, затем помещается между двумя подтаблицами, и две подтаблицы сортируются рекурсивно. В алгоритме 3 показаны детали быстрой сортировки для сортировки таблицы
Алгоритм 3 изящен, но непрактичен. Проблема состоит в том, что рекурсия используется для записи подтаблиц, которые рассматриваются на более поздних этапах, и в худших случаях (когда таблица уже отсортирована) глубина рекурсии может равняться
Лекция № 6
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.190 (0.008 с.) |

 именами, обозначаемыми
именами, обозначаемыми  ,
, 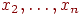 . Каждое имя
. Каждое имя 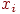 принимает значение из пространства имен, на котором определен линейный порядок. Будем считать, что никакие два имени не имеют одинаковых значений; то есть любые
принимает значение из пространства имен, на котором определен линейный порядок. Будем считать, что никакие два имени не имеют одинаковых значений; то есть любые 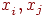 обладают тем свойством, что если
обладают тем свойством, что если 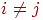 , то либо
, то либо  , либо
, либо 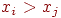 . Ограничение
. Ограничение 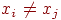 при
при 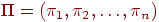 для которой
для которой 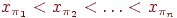 . В задаче полной сортировки требуется полностью определить
. В задаче полной сортировки требуется полностью определить  , хотя обычно это делается неявно путем переразмещения имени в порядке возрастания. В задачах частичной сортировки требуется либо извлечь частичную информацию о
, хотя обычно это делается неявно путем переразмещения имени в порядке возрастания. В задачах частичной сортировки требуется либо извлечь частичную информацию о  для нескольких значений
для нескольких значений  ), либо полностью определить
), либо полностью определить 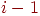 уже отсортированным именами:
уже отсортированным именами:



 независимо от возможных пересылок данных; таким образом, значением
независимо от возможных пересылок данных; таким образом, значением  значения
значения  меняются местами.
меняются местами.  значение
значение 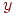 присваивается имени
присваивается имени 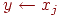 значение имени
значение имени  , которая встречается в различных алгоритмах сортировки, временно нарушает предположение о том, что никакие два имени не имеют одинаковых значений. Однако это условие всегда обязательно восстанавливается.
, которая встречается в различных алгоритмах сортировки, временно нарушает предположение о том, что никакие два имени не имеют одинаковых значений. Однако это условие всегда обязательно восстанавливается. : на этапе
: на этапе  имя
имя  .
.
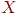 , и просматриваются имена
, и просматриваются имена  ; они сравниваются с
; они сравниваются с 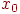 , значение которого
, значение которого  служит для остановки просмотра слева. На рис. 1 работа этого алгоритма проиллюстрирована на примере таблицы из пяти имен.
служит для остановки просмотра слева. На рис. 1 работа этого алгоритма проиллюстрирована на примере таблицы из пяти имен.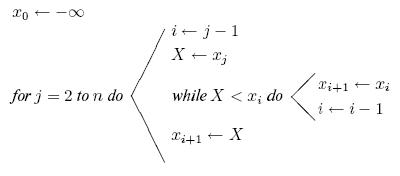
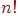 перестановок равновероятны) и лучшем.
перестановок равновероятны) и лучшем.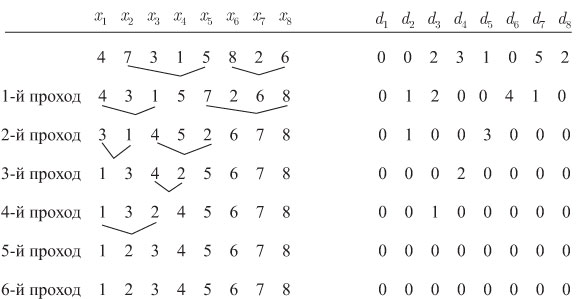
 , значение которой в начале цикла
, значение которой в начале цикла  равно наибольшему индексу
равно наибольшему индексу  , такому, что про имя
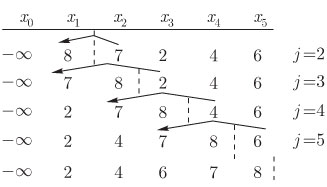
, такому, что про имя 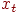 еще не известно, стоит ли оно в окончательной позиции. На рис. 2 показана работа алгоритма на примере таблицы с
еще не известно, стоит ли оно в окончательной позиции. На рис. 2 показана работа алгоритма на примере таблицы с  именами.
именами.
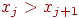 и числа обменов
и числа обменов  . Число обменов равно, как в алгоритме 14.1, числу инверсий: 0 в лучшем случае,
. Число обменов равно, как в алгоритме 14.1, числу инверсий: 0 в лучшем случае, 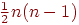 в худшем случае и
в худшем случае и  - в среднем. Рисунок 2 дает возможность предположить, что каждый проход пузырьковой сортировки, исключая последний, уменьшает на единицу каждый ненулевой элемент вектора инверсий и циклически сдвигает вектор на одну позицию влево; легко доказать, что это верно в общем случае, и поэтому число проходов равно единице плюс наибольший элемент вектора инверсий. В лучшем случае имеется всего один проход, в худшем случае -
- в среднем. Рисунок 2 дает возможность предположить, что каждый проход пузырьковой сортировки, исключая последний, уменьшает на единицу каждый ненулевой элемент вектора инверсий и циклически сдвигает вектор на одну позицию влево; легко доказать, что это верно в общем случае, и поэтому число проходов равно единице плюс наибольший элемент вектора инверсий. В лучшем случае имеется всего один проход, в худшем случае -  проходов, где
проходов, где 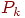 - вероятность того, что наибольшим элементом вектора инверсии является
- вероятность того, что наибольшим элементом вектора инверсии является  . Общее число сравнений имен трудно определить, но можно показать, что оно равно
. Общее число сравнений имен трудно определить, но можно показать, что оно равно  в лучшем случае,
в лучшем случае, 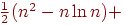
 - в среднем.
- в среднем.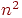 операций, как в среднем, так и в худшем случаях.
операций, как в среднем, так и в худшем случаях.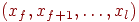 , где
, где  "
"  , все имена находятся в соответствующих частях таблицы и
, все имена находятся в соответствующих частях таблицы и 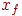 помещается между двумя частями, меняясь при этом местами с
помещается между двумя частями, меняясь при этом местами с  определено и больше, чем
определено и больше, чем  .
.
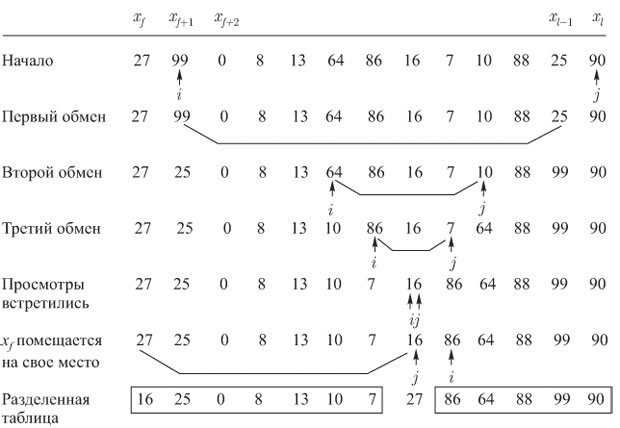
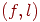 : когда пара находится в стеке, это значит, что нужно сортировать соответствующие
: когда пара находится в стеке, это значит, что нужно сортировать соответствующие 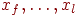 . Алгоритм 4 помещает в стеке большую из двух подтаблиц и немедленно применяет алгоритм к меньшей подтаблице. Это уменьшает глубину стека в худшем случае примерно до
. Алгоритм 4 помещает в стеке большую из двух подтаблиц и немедленно применяет алгоритм к меньшей подтаблице. Это уменьшает глубину стека в худшем случае примерно до 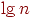 . Заметим, что подтаблицы длины 1 игнорируются и что расщепление подтаблицы делается с использованием случайно выбранного имени в этой подтаблице.
. Заметим, что подтаблицы длины 1 игнорируются и что расщепление подтаблицы делается с использованием случайно выбранного имени в этой подтаблице.



