
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод комплексных амплитуд в формуле Эйлера.
Если в формуле Эйлера:
под φ понимать фазу гармонических колебаний
Из уравнения видно, что решение
где Надо отметить, что метод комплексных амплитуд является, фактически, аналитическим выражением метода векторных диаграмм. Если в последнем методе колебание с частотой
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ Уравнения Максвелла Проанализировав результаты экспериментов Фарадея, Максвелл пришел к выводу, что изменяющееся магнитное поле создает вихревое электрическое поле. Затем Максвелл предположил, что изменяющееся электрическое поле в свою очередь должно создавать вихревое магнитное поле. Так как магнитное поле создается электрическими токами, Максвелл ввел в рассмотрение так называемые токи смещения, которые определяются изменяющимся со временем электрическим полем. Таким образом, согласно теории Максвелла переменные электрическое и магнитное поля взаимосвязаны и одновременно существуют в пространстве. Там, где есть одно из этих полей, непременно есть и другое поле. Существующие вместе переменные электрическое и магнитное поля образуют так называемое электромагнитное поле. Максвелл предложил уравнения, описывающие это поле. Запишем систему уравнений Максвелла для изменяющихся со временем электрического и магнитного полей: div D = q (10.1) (10.2) div B* = 0, (10.3) (10.4) где E - напряженность электрического поля; D - вектор электрической
индукции; E- напряженность магнитного поля; В - магнитная индукция; q - объемная плотность свободных зарядов; j - вектор плотности тока. Второе слагаемое в правой части уравнения (10.3) (10.5) Максвелл назвал плотностью тока смещения.
Уравнение (10.1) выражает собой закон Фарадея. Уравнение (10.2) соответствует теореме Гаусса, которая доказывается в электростатике и переносится без изменения в теорию переменных электрических и магнитных полей (электродинамику). Уравнение (10.3) отличается от аналогичного уравнения из теории постоянного магнитного поля тем, что в его правой части присутствует дополнительное слагаемое jCM - плотность тока смещения. Уравнение (10.4) взято без изменения из магнитостатики. При помощи теорем Стокса и Остроградского - Гаусса уравнения Максвелла можно записать в интегральной форме так: dS =0. В уравнениях (10.6) и (10.8) символ С обозначает произвольный контур, а символ 5 - произвольную поверхность, натянутую на этот контур. В уравнениях (10.7) и (10.9) символ S обозначает произвольную замкнутую поверхность, а символ V - объем внутри этой поверхности. Уравнение (10.6) выражает собой закон электромагнитной индукции Фарадея. Уравнение (10.7) есть теорема Гаусса для вектора электрической индукции. Уравнение (10.8) называется теоремой о циркуляции вектора напряженности магнитного поля, или законом полного тока. Правая часть этого уравнения есть сила тока, протекающего через произвольную поверхность S, натянутую на контур С. Первое слагаемое здесь есть сила тока проводимости, а второе - сила тока смещения. Уравнение (10.9) есть теорема Гаусса для вектора магнитной индукции. Уравнения Максвелла следует дополнить уравнениями, определяющими связь между векторами D и Е и векторами В и Н, а также уравнениями движения носителей тока. Такими уравнениями в большинстве случаев являются где е и /г - абсолютные диэлектрическая и магнитная проницаемости среды, заполняющей пространство, в котором существует исследуемое электромагнитное поле, а - электропроводность вещества. Последнее из этих уравнений выражает закон Ома в дифференциальной форме.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.58 (0.005 с.) |

 ,то каждому такому колебанию S(t) можно поставить в соответствие комплексное число.
,то каждому такому колебанию S(t) можно поставить в соответствие комплексное число.
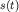 является мнимой частью комплексного выражения:
является мнимой частью комплексного выражения:
 - комплексная амплитуда, которая несет информацию об амплитуде S0 и начальной фазе φ0 колебаний.
- комплексная амплитуда, которая несет информацию об амплитуде S0 и начальной фазе φ0 колебаний. полностью задается вектором S0 то в методе комплексных амплитуд колебание задается числом
полностью задается вектором S0 то в методе комплексных амплитуд колебание задается числом  на комплексной плоскости. Поскольку с комплексными числами удобно и просто производить математические операции, то мы используем это обстоятельство для получения решения уравнения вынужденных колебаний.
на комплексной плоскости. Поскольку с комплексными числами удобно и просто производить математические операции, то мы используем это обстоятельство для получения решения уравнения вынужденных колебаний.


