
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет механических характеристик частотно-регулируемого электроприводаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
2.1 Механическая характеристика при законе U/f=const (f1= 50 Гц)
Под механическими характеристиками понимаем зависимость частоты вращения ротора от момента на валу. Механические характеристики используем для анализа статического и динамического режимов электроприводов. Расчет производен на основе [17]. Для вывода уравнения механической характеристики асинхронного двигателя нужно изобразить его Г-образную упрощенную схему замещения в статических режимах [17], которая изображена на рисунке 2.1. При данной схеме замещения контур намагничивания подключают к зажимам питающего напряжения, что не вносит существенных изменений, которые могут повлиять на точность расчетов.
Uф – первичное напряжение; I1 – фазный ток статора; I'2 – приведенный ток статора; X1 и X'2 – первичное и вторичное приведенные реактивные сопротивления рассеяния; R0 и X0 – активное и реактивное сопротивления контура намагничивания; s – скольжение двигателя; R1 и R'2 – первичное и вторичное приведенные активные сопротивления.
Рисунок 2.1 – Упрощенная схема замещения асинхронного двигателя
Расчет проводится в абсолютных величинах, следовательно, нужно привести относительные параметры двигателя к абсолютным величинам. Для расчета механической характеристики из справочника [27] берутся основные технические данные электродвигателя соединяющего (таблица 2.1).
Таблица 2.1 – Параметры асинхронного двигателя 4AА56B4УЗ
Во-первых, находим номинальный ток электродвигателя:
Затем производим расчет базового сопротивления:
где Чтобы найти сопротивления асинхронного двигателя в абсолютных единицах нужно их значения в относительных единицах умножить на полученное базовое сопротивление (формулы (2.3) и (2.4)):
При построении модели ПЧ-АД в программной среде Matlab, необходимы будут значения индуктивностей статора LS, ротора LR и главного индуктивного сопротивления Lμ. Определим их по следующей общей формуле:
Далее рассчитываем значение индуктивностей по формуле (2.5):
Вращающий момент асинхронного электродвигателя, согласно схеме замещения, определяется следующим выражением:
Для расчета механической характеристики Формула Клосса выглядит следующим образом:
Величина максимального (критического) момента двигателя
Критическое скольжение
Угловая синхронная скорость
Если подставить рассчитанные параметры
Найдем номинальный момент двигателя по формуле (2.6), подставив в нее номинальное скольжение sном:
Номинальным моментом называется момент, возникающий на валу двигателя при номинальной мощности и номинальных оборотах. Для проверки вычислений, номинальный момент можно найти по другой формуле и сравнить значения:
Также необходимо найти начальный пусковой момент асинхронного двигателя по следующей формуле, когда скольжение
Важно учесть, чтобы пусковой момент был больше чем статический момент нагрузки, подключенной к валу двигателя. Для построения естественной механической характеристики
Задавая величину скольжения
Таблица 2.2 – Момент двигателя и значение угловой скорости для частоты
2.2 Механическая характеристика при законе U/f=const (f1= 40 Гц)
Для расчета искусственной механической характеристики асинхронного двигателя при работе с другой частотой, нужно пересчитать индуктивные сопротивления схемы замещения для заданной частоты по следующей формуле:
где
Далее определяем индуктивные сопротивления асинхронного электродвигателя для частоты
Так как нужно сохранять закон
Подставим значения под формулу (2.13):
Определяем максимальный (критический) момент двигателя по формуле (2.7):
Критическое скольжение
Угловая скорость
Получаем выражение искусственной механической характеристики
Для построения искусственной механической характеристики угловой скорости (таблица 2.3).
Таблица 2.3 – Момент двигателя и значение угловой скорости для частоты
2.3 Механическая характеристика при законе U/f=const (f1= 30 Гц)
Определяем индуктивные сопротивления асинхронного двигателя для частоты
Пересчитывается напряжение по формуле (2.13):
Определяем максимальный (критический) момент двигателя по формуле (2.7):
Критическое скольжение
Угловая скорость
Получаем выражение искусственной механической характеристики
Для построения искусственной механической характеристики
Таблица 2.4 – Момент двигателя и значение угловой скорости для частоты
2.4 Механическая характеристика при законе U/f=const (f1= 20 Гц)
Определяем индуктивные сопротивления асинхронного двигателя для частоты
Пересчитывается напряжение по формуле (2.13):
Определяем максимальный (критический) момент двигателя по формуле (2.7):
Критическое скольжение
Угловая скорость
Получаем выражение искусственной механической характеристики
Для построения искусственной механической характеристики Задаваясь величиной скольжения
Таблица 2.5 – Момент двигателя и значение угловой скорости для частоты
На рисунке 2.2 изображены механические характеристики асинхронного двигателя при частотном регулировании скорости при законе управления Данное явление объясняется влиянием падения напряжения на активных сопротивлениях статора. В современных электроприводах имеется компенсация этого падения напряжения при низких скоростях, степень которой можно регулировать. Обычно увеличение напряжения составляет 5-10% от напряжения, необходимого по закону Обеспечение требуемого пускового момента особенно необходимо в системе ПЧ-АД, так как здесь надо учитывать максимальный ток, допустимый для нормальной работы инвертора [17]. Чтобы повысить пусковой момент, необходимо увеличивать мощность преобразователя, что приведет к неустойчивой работе электродвигателя. Если, повысив мощность, не удается получить требуемый пусковой момент, то надо повышать как мощность преобразователя частоты, так и мощность асинхронного двигателя.
Компенсация падения напряжения на активных сопротивлениях статора (IR- компенсация) применяется в большинстве современных преобразователях со скалярным управлением, что является важным при постоянном моменте нагрузки. При малой скорости двигателя и номинальном моменте нагрузки доля напряжения, приходящаяся на активные сопротивления статора, настолько велика, что оставшаяся часть напряжения, создающая магнитный поток, не обеспечивает необходимую перегрузочную способность. Поэтому в диапазоне малых частот следует отходить от закона управления

Рисунок 2.2 – Механические характеристики АД при частотном регулировании
Скольжение определяет различие между угловой скоростью вала двигателя и угловой частотой питающего напряжения. Иногда требуется обеспечить работу механизма с заданной вручную скоростью. При такой задаче можно задать только частоту питающего напряжения, а угловая частота двигателя будет определяться его нагрузкой. При номинальной частоте питающего напряжения скольжение составляет около 3%, таким значением можно пренебречь. При снижении частоты питающего напряжения величина скольжения растет обратно пропорционально этой частоте и пренебрегать им уже нельзя, поэтому в преобразователях со скалярным управлением используется компенсация скольжения, которая основана на увеличении частоты питающего напряжения по сравнению с заданной. Наиболее простой и распространенный метод такой компенсации базируется на линейной аппроксимации рабочего участка механической характеристики АД и оценке момента нагрузки по измеренным значениям токов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 3410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.117 (0.011 с.) |






 – фазное напряжение сети, которое равно 220 В.
– фазное напряжение сети, которое равно 220 В.





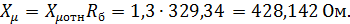



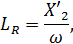
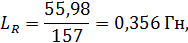
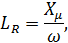


 необходимо применить формула Клосса, которая характеризует зависимость момента асинхронного двигателя от скольжения. Формулу Клосса применяют в тех случаях, когда используется электропривод с асинхронным двигателем. Пользуясь данной формулой, можно легко построить график механической характеристики, ссылаясь только на паспортные данные асинхронного двигателя.
необходимо применить формула Клосса, которая характеризует зависимость момента асинхронного двигателя от скольжения. Формулу Клосса применяют в тех случаях, когда используется электропривод с асинхронным двигателем. Пользуясь данной формулой, можно легко построить график механической характеристики, ссылаясь только на паспортные данные асинхронного двигателя.
 прямо пропорциональна квадрату напряжения, подводимого к статору, и определяется по следующей формуле:
прямо пропорциональна квадрату напряжения, подводимого к статору, и определяется по следующей формуле:

 , при котором двигатель развивает максимальный (критический) момент, рассчитывается как:
, при котором двигатель развивает максимальный (критический) момент, рассчитывается как:

 рассчитывается по следующей формуле:
рассчитывается по следующей формуле:



 в формулу (2.6) получим выражение естественной механической характеристики
в формулу (2.6) получим выражение естественной механической характеристики 



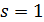 :
:

 рассчитываются значения угловой скорости для заданных величин скольжения по следующей формуле:
рассчитываются значения угловой скорости для заданных величин скольжения по следующей формуле:
 от 0 до 1, определяют соответствующие моменты асинхронного двигателя и значение угловой скорости, после чего полученные значения заносятся в таблицу 2.2.
от 0 до 1, определяют соответствующие моменты асинхронного двигателя и значение угловой скорости, после чего полученные значения заносятся в таблицу 2.2. =50 Гц
=50 Гц


 1,271
1,271




 – индуктивное сопротивление схемы замещения для заданной частоты
– индуктивное сопротивление схемы замещения для заданной частоты  ;
;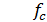 – номинальная частота питания асинхронного двигателя (50 Гц);
– номинальная частота питания асинхронного двигателя (50 Гц); – индуктивное сопротивление при номинальное частоте (50 Гц).
– индуктивное сопротивление при номинальное частоте (50 Гц). =40 Гц по формуле (2.12):
=40 Гц по формуле (2.12):
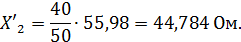
 , пересчитывается также и напряжение сети по формуле:
, пересчитывается также и напряжение сети по формуле:
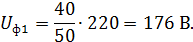





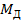


 = 30 Гц по формуле (2.12):
= 30 Гц по формуле (2.12):





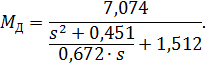
 =20 Гц по формуле (2.12):
=20 Гц по формуле (2.12):


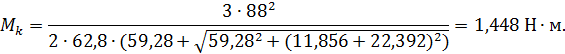



 1,421
1,421
 , аппроксимируя ее несколькими отрезками прямых. Этот метод позволяет компенсировать падение перегрузочной способности. Метод IR- компенсации является приблизительным, не учитывает особенностей конкретного механизма. При его использовании иногда возникает перекомпенсация, которая приводит к большим броскам тока при пуске двигателя [21].
, аппроксимируя ее несколькими отрезками прямых. Этот метод позволяет компенсировать падение перегрузочной способности. Метод IR- компенсации является приблизительным, не учитывает особенностей конкретного механизма. При его использовании иногда возникает перекомпенсация, которая приводит к большим броскам тока при пуске двигателя [21].


