
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель системы ПЧ-АДСодержание книги
Поиск на нашем сайте
При составлении математической модели ПЧ-АД, схема силовых цепей которого показана на рисунке 4.1, будет использоваться метод структурного моделирования, при котором будут выделены отдельные элементы. К ним можно отнести АД, АИН с выходным реактором, неуправляемый выпрямитель с входным коммутирующим реактором и LC- фильтром на выходе [19]. Для модели асинхронного двигателя с короткозамкнутым ротором можно написать следующую систему скалярных уравнений:
где
Насыщение магнитной цепи машины в модели АД учитывается переменным коэффициентом
Рисунок 4.1 – Схема силовых цепей системы ПЧ-АД
АИН с ШИМ представляет собой сложное нелинейное дискретное устройство. Несущая частота АИН находится в диапазонах от 2 до 16 кГц, поэтому для построения математической модели АИН используется метод выделения полезных сигналов путем усреднения мгновенных значений переменных в пределах периода несущей частоты [29]. В этом случае инвертор напряжения будет описываться следующими уравнениями:
где
Выходные реакторы выражается следующими уравнениями:
где Чтобы выделить главные особенности неуправляемого выпрямителя используют математическую модель, которая отображает только основную гармонику коммутационной функции выпрямителя.
Математическая модель неуправляемого выпрямителя с входным реактором представляется следующей системой уравнений:
где
Модель LC-фильтра на выходе неуправляемого выпрямителя определяется линейными уравнениями вида:
где
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.142.62 (0.009 с.) |















 ,
,  ,
,  ,
,  ,
,  ,
,  – преобразованные напряжения, токи и полные потокосцепления обмотки статора;
– преобразованные напряжения, токи и полные потокосцепления обмотки статора; ,
,  ,
,  ,
,  – преобразованные токи и полные потокосцепления обмотки ротора;
– преобразованные токи и полные потокосцепления обмотки ротора; ,
,  ,
,  ,
,  – результирующие токи намагничивания и главные потокосцепления.
– результирующие токи намагничивания и главные потокосцепления.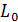 , который зависит от тока намагничивания и определяется как
, который зависит от тока намагничивания и определяется как  , где
, где  – модуль результирующего вектора намагничивающих токов,
– модуль результирующего вектора намагничивающих токов,  . При рассмотрении магнитной цепи коэффициент
. При рассмотрении магнитной цепи коэффициент 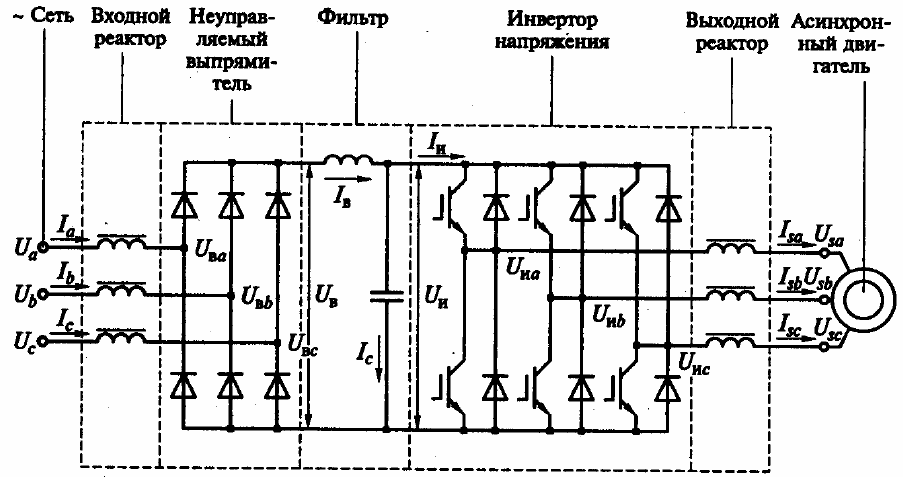





 ,
,  – преобразованные задающие воздействия;
– преобразованные задающие воздействия; ,
,  – усредненные коммутационные функции;
– усредненные коммутационные функции; – амплитуда опорного сигнала;
– амплитуда опорного сигнала; – напряжение источника питания инвертора;
– напряжение источника питания инвертора; – усредненный ток питания инвертора;
– усредненный ток питания инвертора; ,
,  – усредненные выходные напряжения инвертора;
– усредненные выходные напряжения инвертора; ,
, 
 ,
,  – активное сопротивление и индуктивность выходного реактора.
– активное сопротивление и индуктивность выходного реактора.







 ,
,  ,
,  ,
,  ,
,  – преобразованные основные гармоники напряжений на силовом входе неуправляемого выпрямителя;
– преобразованные основные гармоники напряжений на силовом входе неуправляемого выпрямителя; ,
,  – преобразованные основные гармоники коммутационных функций неуправляемого выпрямителя;
– преобразованные основные гармоники коммутационных функций неуправляемого выпрямителя; – угол поворота обобщенного вектора коммутационной функции выпрямителя;
– угол поворота обобщенного вектора коммутационной функции выпрямителя; – угол поворота системы координат;
– угол поворота системы координат; ,
,  – напряжение и ток на выходе выпрямителя;
– напряжение и ток на выходе выпрямителя; ,
,  – активное и индуктивное сопротивление входного реактора.
– активное и индуктивное сопротивление входного реактора.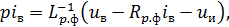

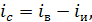
 ,
,  – активное сопротивление и индуктивность сглаживающего реактора LC-фильтра;
– активное сопротивление и индуктивность сглаживающего реактора LC-фильтра; – емкость конденсаторной батареи фильтра;
– емкость конденсаторной батареи фильтра; – ток конденсатора фильтра [19, с.36].
– ток конденсатора фильтра [19, с.36].


