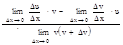Определение производной, её физический и геометрический смысл. Связь дифференцируемости и непрерывности.

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

y=f(x), х?D(f), х+∆x?D(f) ∆y=f(x+∆x)-f(x)

Опр. lim(∆x→0) ∆y/∆x наз производной данной ф-ции, (обозначается f ' (x), y ' _x, dy/dx, df(x)/dx)

y'=lim(∆x→0) ∆y/∆x

y'=lim(∆x→0) (f(x+∆x)-f(x))/ ∆x

 

Физический смысл производной

y=f(x) определяет скорость изменения ф-ции в момент х

Геометрический смысл

f(x)=tg – угловой коэффициент касательной

Дифференцируемость ф-ции. Связь диффер-ти и непрерывности

Производная f '(x ₀) функции f в точке x ₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x ₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

 

Для дифференцируемой в x ₀ функции f в окрестности U (x ₀) справедливо представление

f (x) = f (x ₀) + f '(x ₀)(x − x ₀) + o (x − x ₀) при

По опр y'=lim(∆x→0) ∆y/∆x

Опр. Ф-я y=f(x) наз дифференцируемой в т х, если в этой т-ке существует производная в этой точке.

 

 

Ф-ция наз диффер-емой на отрезке [а,b], если она диф-ма в каждой т-ке этого отрезка.

Теорема (связь между диф-тью. и непрерывностью в т.)

Если ф-я диф-ма в т.х, то она непрерывна в этой точке. Обратное неверно!

 

Основные правила дифференцирования.

Пусть ф-ции u=u(x) и v=v(x) дифф-мые ф-ции.

1.(u ± v)' =u' ± v'. Док-во для разности f(x)=u(x)-v(x). Найдем приращение из y+∆y=u+∆u-(v+∆v),

∆y=(u+∆u)-(v+∆v)-(u-v)+ ∆u-∆v и вычислим предел lim(∆x→0) ∆y/∆x=lim(∆x→0) (∆u-∆v)/ ∆x=

lim(∆x→0) ∆u/∆x-lim(∆x→0) ∆v/∆x=u ' (x)-v ' (x).

2.(u v)'=v'u*u'v. Док-во. Рассмотрим произведение 2-х ф-ций f(x)=uv и предположим, что ф-ции u(x) и v(x) дифференцир-мы, тогда y+∆y=(u+∆u)*(v+∆v). Найдем приращение произведения и вычислим предел

lim(∆x→0) ∆y/∆x=lim(∆x→0) ((u+ ∆u)(v+∆v)-uv)/ ∆x=lim(∆x→0) (uv+v∆u+u∆v+∆u∆v-uv)/ ∆x=v*lim(∆x→0) ∆u/∆x+u*lim(∆x→0) ∆v/∆x+lim(∆x→0) ∆u∆v/∆x=u ' v+v ' u

Т.к. произведение есть бесконечно малая более высокого порядка, чем приращение, поэтому последний предел =0. А два первых предела по определению есть производные.

3.(u/v)'=(u'v-v'u)/v². Док-во Рассм. частное двух ф-ций y=u(x)/v(x), v(x) ≠ 0 и предположим, что ф-ции u(x) и v(x) диф-мы. Приращению аргумента соответствует значение ф-ции x+∆x =>y+∆y, которое = y+∆y=(u+∆u)/(v+∆v). Тогда приращение частного 2-х ф-ции представляется в виде ∆y=(u+∆u)/(v+∆v)-u/v. Найдем производную y ' =lim(∆x→0) ∆y/∆x=(u/v) ' =lim(∆x→0) (uv+v∆u-uv-u∆v)/ ∆x(v∆v)v.

Почленно числитель разделим на ∆x, учитывая, что пределы отношений ∆u, ∆v к приращению аргумента при ∆x→0 являются производными получим

y '= =

 

 

=(u'v-v'u)/v²

4.

 

5. y=f(x) и x=g(y) – взаимно-обратные ф-ции, то y_x ' =1/x_y '

Следствия.

1) (cu)'=cu', где с=const

2) (u*v*w)=u'vw+v'uw+w'uv