Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы интегрирования:метод разложения,метод замены переменной. ⇐ ПредыдущаяСтр 7 из 7
1) ∫f1(x)+f2(x)dx=∫f1(x)dx+∫f2(x)dx 2) ∫Cf(x)dx=C∫f(x)dx 3) Если ∫f(x)dx= F(x)+C,то ∫f(u)du = F(u)+C, где u=φ(x) I. ∫λ1f1(x)+…+λnfn(x)dx= λ1∫f1(x)dx+ λn∫fn(x)dx II. Метод замены переменной ∫f(x)dx=|x=φ(t), dx=φ’(t)dt|=∫f(φ(t))φ’(t)dt Группы интегралов берущихся с помощью одной и той же подстановки. I. II. III.
IV. { замена
V.
Интегралы от квадратного трехчлена. Интегрирование по частям. 1.
2.
3. + ln (сумма 2х интегралов)
4.
5.
Интегрирование по частям. u=u(x) и v=v(x)-дифф-емые ф-ци), du*v=u*dv+v*du→u*dv=duv-v*du→
Тригонометрические подстановки: 1) 2) 3) Интегрирование рациональных дробей, некоторых иррациональных функций
R(x)=P(x)/Q(x),P(x),Q(x)-многочлены степени m и n, если m<n-правильная рац.дробь, если m=>n-неправ.рац дробь P(x)/Q(x)-неправ.рац.дробь→P(x)/Q(x)=F(x)+ P1(x) /Q(x) Среди правильных рациональных дробей разделяют 4 вида простых или простейших дробей 1) 3) Теорема. Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей Разложение правильной дроби на простые связано с разложением знаменателя на множители. (m-степ, n- степ,m<n) Установлено, что каждому множителю
Т.о. зная разложение знаменателя на множители, мы знаем знаменатели тех простых дробей, на сумму которых разлагается данная рациональная дробь; числители этих простых дробей зависят от неопределенных коэффициентов. 1) 2) неправильная 3) разлагаем правильную на сумму простых дробей 4) берем инт-л от каждого слагаемого Т.о. интегралы от любой рациональной функции берутся
Интегралы от некоторых иррациональных выражений. R ( I. II. Интегрирование некоторых тригонометрических ф-ций 1.
2.
3. Формулы понижения степени:
Тригонометрические подстановки: 1) 2) 3) Определенный интеграл и его свойства Пусть функция f(x) задана на отрезке [а,b] выполним следующие действия: 1)Разбить [а,b] на части d=max
2) 3)составим интегральную сумму Римана
Если существует предел при d стремящимся 0 от И обозначается
Замечания: Предел интегрирования суммы (определенный интеграл) не зависит от способа разбиения [а,b] на части и выбора промежуточных точек Достаточное условие интегрируемости Т. Если f(x) непрерывна на [а,b]то она интегрируема на этом отрезке Геометрический смысл
1) f(x)≥0
2) f(x) – знакопеременна на [а,b]
По определению полагаем 1) Свойства определенного интеграла: 1) 2) 3) 4) Если точка С разбивает [а,b] на [а,с] и [с,b], то интеграл
5)
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.34 (0.015 с.) |





 }
}


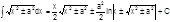
 ;
; 













 - ф-ла интегрирования по частям.
- ф-ла интегрирования по частям. ,
,

 2)
2) 
 4)
4) 
 в разложении знаменателя соответствует сумма k простых дробей вида
в разложении знаменателя соответствует сумма k простых дробей вида , а каждому множителю
, а каждому множителю  соответствует сумма s простых дробей вида:
соответствует сумма s простых дробей вида:
 правильная или неправильная
правильная или неправильная выделяем целую часть
выделяем целую часть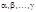 ) – рациональное ф-ция от
) – рациональное ф-ция от 
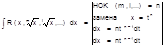
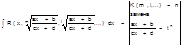
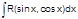

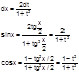


 (m и n – четные)
(m и n – четные)
 ,
,



 -разбиение [а,b], d-диаметр разбиения
-разбиение [а,b], d-диаметр разбиения рассмотрим произвольную точку
рассмотрим произвольную точку  и назовем ее промежуточная, а также найдем значения f(x) в этой точке
и назовем ее промежуточная, а также найдем значения f(x) в этой точке
 (lim(d→0)In) то он называется определенным интегралом по Риману от f(x) по отрезку[а,b]
(lim(d→0)In) то он называется определенным интегралом по Риману от f(x) по отрезку[а,b]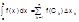

 [а,b], то
[а,b], то
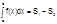

 2)
2)