
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые последовательности. Предел последовательности. Предел функции.Стр 1 из 7Следующая ⇒
Числовые последовательности. Предел последовательности. Предел функции. Определение: Числовой последовательностью назыв множество чисел, пронумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров. у1, у2, …, уn={yn}→yn=f(n), где у1, у2 –члены, yn=f(n) –общий член последов. Определение: Число а назыв пределом последов, если
Геометрическая интерпретация y=f(x) – ф-ция, х - аргумент ф-ции, х→а, f(x) →А, А предел ф-ции Определение: числа А назыв. пределом ф-ции f(x) при х→а, если Замечание: 1) х→а как угодно; 2) f(x) в точке а может быть и не определена. Определение: числа А назыв. пределом ф-ции f(x) при х→∞, если Теорема: Любая функция, имеющая предел, является ограниченной.
Теоремы о пределах. Односторонние пределы. Теорема 1: Пусть lim{x→a}f(x)=А и lim{x→a}g(x)=В, тогда 1)lim{x→a}(f(x)+g(x)) = А+В; 2)lim{x→a}(f(x)*g(x)) = А*В; 3)lim{x→a}(f(x)/g(x)) =А/В Теорема 2: lim f1(x)= А1 lim f2(x) = А2, f1(x)<=f2(x), Теорема 3: lim f1(x)=А, lim f2(x) = А, f1(x)<f(x)<f2(x) => lim f(x) =A Определение: если при вычислении предела lim{x→a}f(x) при х→а, Х остаётся всё время меньше (больше) а, то предел называется левым(правым) – оба односторонние. Замечание: 1) Если сущ-ют и равны м/у собой односторонние пределы, то они равны пределу f(x), при х→а. 2) Если существует предел данной функции, то существует и его односторонние пределы. Первый и второй замечательные пределы. Первый замечательный предел
Доказательство
Рассмотрим односторонние пределы Пусть (1) (где SsectOKA — площадь сектора OKA)
(из Подставляя в (1), получим:
Так как при
Умножаем на sin x:
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Второй замечательный предел
Доказательство второго замечательного предела: Доказательство второго замечательного предела для случая последовательности (т.е. для натуральных значений x)
По формуле бинома Ньютона: Полагая
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
Поэтому Итак, последовательность ограничена сверху, при этом Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, т.е. докажем, что 1. Пусть Отсюда следует:
Если
По признаку (о пределе промежуточной функции) существования пределов 2. Пусть
Из двух этих случаев вытекает, что Точки разрыва. Если для y=f(x) рав-во (3): f(x0 -0)+f(x0 +0) =f(x0) нарушается, то х0 - точка разрыва Характер нарушения рав-ва (3) кладется в основу классификации точек разрыва: 1. а) если f(x0 -0) и f(x0 +0) сущ-ют и f(x0 -0) ≠f(x0 +0), то х0 - наз. т-кой разрыва 1-го рода с конечным скачком. Разность f(x0 -0)-f(x0 +0) наз скачком ф-ции в т.х 0 b)Если в т. х f(x0 -0) = f(x0 +0) ≠f(x0), то х0 наз т-кой разрыва 1 рода устранимой.
2. Если хотя бы один из пределов f(x 0-0) или f(x0 +0) не сущ-ет или =∞, то х0 наз т-кой разрыва 2-го рода ф-ции y=f(x) Теоремы о непрерывных ф-ях. Т 1. Если y=f(x) и y=g(x) непрерывны в т. x 0, то в этой т-ке непрерывны также f(x) ±g(x), f(x)*g(x), f(x)/g(x),(g(x0) ≠0) Т 2. Сложная ф-ция, составленная из конечного числа непрерывных ф-ций непрерывна. Т 3. Ф-я обратная к непрерывной и монотонной ф-ции непрерывна. Вывод: Все элементарные ф-ции непрерывны в областях, где они определены Геометрический смысл
f(x)=tg – угловой коэффициент касательной Следствия. 1) (cu)'=cu', где с=const 2) (u*v*w)=u'vw+v'uw+w'uv Ур.кас-ой. нормали. Касательная - предельное положение секущей. Нормаль-прямая, перпендик. касательной в точке. Геом.смысл производной f’(x)=tgA=K Из аналит.геом Ур.кос:y-y0=f’(x0)(x-x0) K=-1/f’(x0) Ур.нормали y-y0=-(x-x0)/f’(x0) Диф-ы сложных ф-ий Расм. Сложную ф-ию {y=f(u),u=g(x)} Y=f(g(x))=F(x) dy=F’(x)dx=f’ (u)g’(x)dx=f’(u)du Св.инвариантности: диф-л 1-го порядка сохр. свою форму независимо от того будет ли аргумент ф-ии независимой переменной или функцией. Для диф-в высшего порядка это св-во не сохраняется
Дост. признак экстремума Пусть т. Х0-критическая (f’(x0)=0, несущ.) если Правило нахождения экстремума 1. D(x)? 2.f’(x)? 3. крит точки? 4. разбить D(f) точками (+-) 5. Ответ Дост. признак экстремума Пустьf’(x0)=0, f’’(x0)≠0 то если f’’(x0)<0 то x0-т.max, f’’(x0)>0 то x0-т.min
Вертикальные асимптоты
Наклонная асимптота Прямая y=kx+b-накл.ассимп графика ф-ии y=f(x) если f(x)-kx-b→0, т. к. по формуле нахождения расстояния от точки то графика
Теорема Для того чтоб прямая y=kx+b была наклон асимп.грфика ф-ии y=(x) необходимо и достаточно чтобы Горизонтальная Если при нахождении накл.ас. к=0 то y=b- г.о.
Предел и непрерывность. Определение. Окрестностью радиуса r точки М0(х0,y0) называется множество точек М(x,y) координаты которых удовлетворяют неравенству
Определение. Число А называется пределом функции f(x,у) при М(х;у)->М0(х0,у0), если для любого наперед заданного ε > 0 существует такой радиус r, что для всех точек из окрестности радиуса r точки М0 выполняется: | f (x,y) - f (x0,y0)| < E и обозначается A=lim {x→х0 y→у0} f (x;y) причем x;y стремятся к точке М0 произвольным образом. Замечание. В некоторых случаях предел функции зависит от порядка вычисления предела по аргументам. Определение. Функция f (х;у) называется непрерывной в точке M0, если в окрестности этой точки выполняется соотношение (3) Lim{ x → х0; y → у0 } f(x,y) = f(x0;y0) Определение. Функция, непрерывная во всех точках области, называется непрерывной в этой области, преобразуем соотношение Lim { ∆x →0 ∆y→0 }[ f(x,y) - f(x0;y0)]=0 Так как x → x0 и y → y0, x=x0 + ∆x, y =y0 + ∆y, ∆x→0, ∆y→0 То имеем Lim{ ∆x→0, ∆y→0 } [ f(x0 + ∆x, y0 + ∆y) - f(x0;y0)]=0 Определение. Если предел полного приращения при ∆ х → 0 и ∆ y → 0 равняется нулю, то функция называется непрерывной в точке x0,y0. Определение. Точка разрыва x1,y1, может быть в следующих случаи: 1.Функция f(x,у) в точке х1, у1 не определена. 2.Функция f(x, у) определена в самой точке и в окрестности ее, a предел не существует З.Существует предел функции, функция определена в точке в и ее окрестности, но не выполняется равенство (3) при х → х1, у → y1
II. Метод замены переменной
∫f(x)dx=|x=φ(t), dx=φ’(t)dt|=∫f(φ(t))φ’(t)dt Геометрический смысл
1) f(x)≥0
2) f(x) – знакопеременна на [а,b]
По определению полагаем 1) Свойства определенного интеграла: 1) 2) 3) 4) Если точка С разбивает [а,b] на [а,с] и [с,b], то интеграл
5) Если
Тройной интеграл Тройным интегралом называют кратный интеграл с
В прямоугольных координатах Числовые последовательности. Предел последовательности. Предел функции. Определение: Числовой последовательностью назыв множество чисел, пронумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров. у1, у2, …, уn={yn}→yn=f(n), где у1, у2 –члены, yn=f(n) –общий член последов. Определение: Число а назыв пределом последов, если
Геометрическая интерпретация y=f(x) – ф-ция, х - аргумент ф-ции, х→а, f(x) →А, А предел ф-ции Определение: числа А назыв. пределом ф-ции f(x) при х→а, если Замечание: 1) х→а как угодно; 2) f(x) в точке а может быть и не определена. Определение: числа А назыв. пределом ф-ции f(x) при х→∞, если Теорема: Любая функция, имеющая предел, является ограниченной.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.179 (0.104 с.) |
 >0, сколь угодно малого
>0, сколь угодно малого 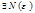 , что для всех n> N(
, что для всех n> N( ), выполняется
), выполняется  , при этом
, при этом =a, (a-ε;a+ε) - окрестность
=a, (a-ε;a+ε) - окрестность >0, сколь угодно малого,
>0, сколь угодно малого,  >0, что для всех x, для которых выполняется условие
>0, что для всех x, для которых выполняется условие  <
<  , имеет место
, имеет место  <
<  =A
=A , что для всех x,|x|>N, выполняется.
, что для всех x,|x|>N, выполняется.  <
<  =A
=A x
x  D(f) => A1<A2
D(f) => A1<A2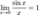



 и
и 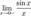 и докажем, что они равны 1
и докажем, что они равны 1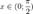 . Отложим этот угол на единичной окружности (R = 1).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что:
. Отложим этот угол на единичной окружности (R = 1).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что:



 : | LA | = tg x)
: | LA | = tg x)
 :
:










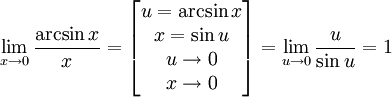



 Докажем вначале теорему для случая последовательности
Докажем вначале теорему для случая последовательности 

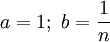 , получим:
, получим:
 (1)
(1) убывет, поэтому величины
убывет, поэтому величины  возрастают. Поэтому последовательность
возрастают. Поэтому последовательность  — возрастающая, при этом
— возрастающая, при этом (2).
(2).
 .
. .
.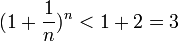 (3).
(3). выполняются неравенства (2) и (3):
выполняются неравенства (2) и (3):  .
.

 . Рассмотрим два случая:
. Рассмотрим два случая: . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами:  , где n = [ x ] - это целая часть x.
, где n = [ x ] - это целая часть x. , поэтому
, поэтому .
.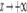 , то
, то 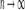 . Поэтому, согласно пределу
. Поэтому, согласно пределу  , имеем:
, имеем:
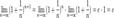 .
. .
. . Сделаем подстановку − x = t, тогда
. Сделаем подстановку − x = t, тогда
 .
. для любого x.
для любого x.
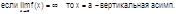 -
-

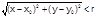

 [а,b], то
[а,b], то
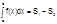

 2)
2) 
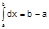






 .
. Здесь
Здесь  — элемент объема в рассматриваемых координатах.
— элемент объема в рассматриваемых координатах. , где
, где  является элементом объема в прямоугольных координатах.
является элементом объема в прямоугольных координатах.


