
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование неявных функции
1 Функция одного аргумента. Пусть дана некоторая непрерывная функция y = f(x) задана в неявной форме, то есть в виде уравнения F(x;y)=0 (уравнение 1). Требуется найти производную Доказательство. Первый способ. Придавая аргументу х приращение
2 Функция многих переменных, заданной неявно. Пусть задана функция трех переменных F (x;y;z) причем х;у – независимые переменные, а функция z зависит от х;у и задана неявно. При дифференцировании по х, переменную у считаем постоянной, поэтому можно предполагать, что z –неявная функция относительно одного аргумента х; F(x,const,z)=0. Следовательно, к этому уравнению можно применить уравнение (2), где вместо у возьмем z, тогда
Обобщим формулу (3). Пусть функция u многих аргументов задана неявно F (x;y;z;..;t;u)=0, тогда частные производные определяются по формуле Таким образом, частные производные функции нескольких переменных, заданных неявно, равны отношению частных производных по одной переменной к частной производной по переменной функции, взятой с обратным знаком.
23. Экстремум функции двух переменных. Необходимые и достаточные условия экстремума Необходимый признак экстремума: Если в точке
24. Первообразная, неопределенный интеграл, его свойства, таблица интегралов. Ф-ция F(x) называется первообразной для f(x) на некотором интервале. F’(x)=f(x) Теорема. Если ф-ция f(x) имеет хотя бы одну первообразную F(x),то ф-ция F(x)+C также является первообразной f(x). Совокупность всех первообразных для f(x) назыв. неопределенным интегралом от этой ф-ции и обозначается. ∫f(x)dx=F(x)+C f(x)-подынтегральная ф-ция, f(x)dx- подынтегральное выражение. Свойства. 1) (∫f(x)dx)’=(F(x)+C)’=F’(x)=f(x) 2) d∫f(x)dx =(∫f(x)dx)’dx=f(x)dx 3) ∫df(x)dx=∫f’(x)dx =f(x)+C Теорема. Если f(x) непрерывна на интервале (а,b),то она имеет на нем первообразную. Геометрический смысл первообразной. ∫f(x)dx =F(x)+C=y эти уравнения определяют множества кривых, которые назыв. интегральными кривыми. Для того чтобы выделить из семейства интегральных кривых одну, задают начальные условия, что равносильно заданию точки, через которую проходит искомая интегральная кривая.
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.54 (0.008 с.) |
 , используя уравнение (1) как функцию двух переменных. Теорема. Если у непрерывная функция от х задана неявно и существуют частные производные
, используя уравнение (1) как функцию двух переменных. Теорема. Если у непрерывная функция от х задана неявно и существуют частные производные  ,причем
,причем  , тогда справедлива формула:
, тогда справедлива формула:  (Ур 2)
(Ур 2) используя определение частной производной и т.д. Второй способ. Представим уравнение (1) как сложную функцию двух переменных z = F (x;y) и y = y(x). Найдем ее полную производную
используя определение частной производной и т.д. Второй способ. Представим уравнение (1) как сложную функцию двух переменных z = F (x;y) и y = y(x). Найдем ее полную производную  . На самом деле функция z – тождественный ноль, поэтому ее полная производная равна нулю.
. На самом деле функция z – тождественный ноль, поэтому ее полная производная равна нулю.  . Откуда найдем
. Откуда найдем или
или  Теорема доказана.
Теорема доказана. аналогично,
аналогично,  (Ур 3)
(Ур 3)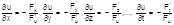
 дифференцируемая функция
дифференцируемая функция  имеет экстремум, то ее частные производные в этой точке равны нулю:
имеет экстремум, то ее частные производные в этой точке равны нулю: ,
,  . Доказательство: Допустим, что функция
. Доказательство: Допустим, что функция  имеет в точке
имеет в точке  экстремум. Согласно определению экстремума функция
экстремум. Согласно определению экстремума функция  , как функция одного
, как функция одного  достигает экстремума при
достигает экстремума при  . Как известно, необходимым условием для этого является обращение в нуль производной от функции
. Как известно, необходимым условием для этого является обращение в нуль производной от функции  при
при  , т. е.
, т. е. . Аналогично функция
. Аналогично функция  при постоянном
при постоянном  , как функция одного
, как функция одного  , достигает экстремума при
, достигает экстремума при  . Значит,
. Значит,  Что и требовалось доказать.Точка
Что и требовалось доказать.Точка  , координаты которой обращают в нуль обе частные производные функции
, координаты которой обращают в нуль обе частные производные функции 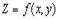 , называется стационарной точкой функции
, называется стационарной точкой функции  . Уравнение касательной плоскости к поверхности
. Уравнение касательной плоскости к поверхности  :
:  для стационарной точки
для стационарной точки  принимает вид
принимает вид  . Следовательно, необходимое условие достижения дифференцируемой функцией
. Следовательно, необходимое условие достижения дифференцируемой функцией  экстремума в точке
экстремума в точке  геометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.Для отыскания стационарных точек функции
геометрически выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке параллельна плоскости независимых переменных.Для отыскания стационарных точек функции  нужно приравнять нулю обе ее частные производные
нужно приравнять нулю обе ее частные производные  ,
,  . (*) и решить полученную систему двух уравнений с двумя неизвестными. Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.Пусть точка
. (*) и решить полученную систему двух уравнений с двумя неизвестными. Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.Пусть точка  является стационарной точкой функции
является стационарной точкой функции  , т. е.
, т. е.  Вычислим в точке
Вычислим в точке  значение вторых частных производных функции
значение вторых частных производных функции 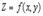 и обозначим их для краткости буквами A, B и C:
и обозначим их для краткости буквами A, B и C:  Если
Если  , то функция
, то функция  имеет в точке
имеет в точке  экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия
экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия  следует, что A и C обязательно имеют одинаковые знаки). Если
следует, что A и C обязательно имеют одинаковые знаки). Если  , то точка
, то точка  не является точкой экстремума.Если
не является точкой экстремума.Если  , то неясно, является ли точка
, то неясно, является ли точка  точкой экстремума и требуется дополнительное исследование.
точкой экстремума и требуется дополнительное исследование.


