Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические уравнения, сводящиеся к простейшимСодержание книги Поиск на нашем сайте
Тригонометрическими уравнениями называются уравнения, содержащие тригонометрические функции от неизвестной величины. Каждое значение, при подстановке которого вместо неизвестной величины получается верное равенство, называется решением или корнем тригонометрического уравнения. Решить тригонометрическое уравнение значит найти все его корни или доказать, что уравнение корней не имеет. Пример 4.1. Решить уравнение
Решение. Заменим
Подставим полученное выражение в уравнение (а) и преобразуем его, получим
Полученное уравнение сводится к решению двух уравнений:
Первое уравнение:
Второе уравнение, рис. 4.10:
Откуда
Итак, уравнение (а) имеет два корня
Пример 4.2. Решить уравнение
Решение. Заменим
Подставим полученное выражение в уравнение (б) и преобразуем его, получим
Полученное уравнение содержит только функцию
Таким образом, равенство
Второе уравнение (см. рис. 4.11): Итак, уравнение (б) имеет три корня
Пример 4.3. Решить уравнение
Решение. Заменим
Подставим полученное выражение в уравнение (в), получим
Отсюда
Разделим полученное уравнение на
Полученное уравнение содержит только функцию Пусть
1. 2. Справка: Пример 4.4. Решить уравнение:
Решение. Имеем
По общим формулам запишем ответ (числовые значения приведены в таблице 4.11):
Итак, получили
Таблица 4.11
Пример 4.5. Решить уравнение
Решение. Пусть
Вычислим корни полученного уравнения
Уравнение (а) имеет единственное решение Имеем:
Пример 4.6. Решить уравнение
Решение. Пусть
Разложим левую часть на множители, получим
откуда
Имеем 1. 2. Пример 4.2. Решить уравнение
Решение. Выразим косинус через синус
Введем обозначения:
Освободив уравнение от радикалов, получим
Имеем
Первое уравнение:
Замечание. Из общей формулы Второе уравнение:
Итак, заданное уравнение (а) имеет два корня
Приложение тригонометрических функций В физике, механике, технике, химии, биологии и др. науках изучаются периодические движения, или колебания. Колебания – такие изменения состояния исследуемой системы или объекта наблюдения, которые характеризуются определенной степенью повторяемости во времени, возвращаемости к начальному состоянию. Периодом колебаний называется промежуток времени, в течение которого совершается одно полное движение. Следовательно, для описания периодических процессов следует вводить функции, зависящие от времени, т. е. параметра Пусть периодические движения проходят вдоль одного выделенного направления, например, вдоль оси Рассмотрим примеры их механики. Определение траектории движения точки. Геометрическое место последовательных положений при движении точки в интервале времени В частности, движение точки на интервале времени Пример 5. 1. Точка
1. Определить траекторию движения точки. 2. Провести анализ движения точки по заданной траектории. 3. Вычислить среднюю скорость точки Решение. I. Определим траекторию движения точки. Дляэтого в декартовой системе координат определим область, в которой движется точка, т.е. область значений заданной функции
Введем обозначение:
Функции
Построим график заданной функции Точка движется в евклидовом пространстве
Рис. 5.1 II. Проведем анализ движения точки по заданной траектории в евклидовом пространстве
1. При 2. При 3. При 4. При
За Итак, траекторией движения точки 3. Вычислим среднюю скорость точки Вычислим среднюю скорость точки Таблица 5.1
Вычислим среднюю скорость точки
Решение. Декартовую систему координат I. Определим траекторию точки А. Положение точки А определяется координатами
Тем самым определили область, в которой точка движется (рис. 5.4). Получим аналитическую функцию, которая является траекторией точки. Для этого исключим параметр t из уравнений движения (a). Для этого возводим в квадрат каждое уравнение (а) и сложим их между собой. Имеем:
Учитывая, что
Итак, точка
Построим графики функций
Рис. 5.5 Опишем движение точки А: 1. При 2. При Вычислим среднюю скорость точки Вычислим числовые значения (рис. 5.6):
Тогда:
II. Определим траекторию точки B. Уравнение движения точки В в системе координат
Дляпостроения траектории в декартовой системе координат
Траекторией движения точки
Рис. 5.7
Проведем анализ движения точки Таблица 5.2
Движение повторяется до бесконечности. От начала движения до возвращения в исходное положение проходит Нетрудно видеть (рис. 5.6, б), что: – при – при – при Итак, траекторией движения точки Пример 5.3. Движение точки M по плоскости Оху задано уравнениями движения
Построить траекторию движущейся точки, вычислить среднюю скорость движения точки Решение. Движение точки задано параметрическими уравнениями, параметром является время Построим графики заданных функций в системах координат Графиком функции
Рис. 5.8 Проведем анализ движения точки по оси – при – при – при Далее движение точки повторяется до бесконечности. Графиком функции Проведем анализ движения точки по оси – при
Функции
получаем (рис. 5.9):
Выделяем на плоскости
Тем самым мы определили область, в которой точка движется. Получим аналитическую функцию
Для этого делим первое уравнение системы (а’) на 2, второе – на 4. Далее, возводим полученные выражения в квадрат и складываем их между собой:
Учитывая, что
Получили каноническое уравнение эллипса. Итак, траекторией движущейся точки является эллипс (рис. 5.9). Подставляя в (а) значение
Точка в начальный момент времени занимает положение
Пример 5.4. Движение точки в плоскости
где Требуется задать движение точки в явном виде; вычислить скорость, нормальную и касательную составляющие ускорения, радиус кривизны траектории в соответствующей точке для момента времени Решение. Дляпостроения траектории в декартовой системе координат определим область значений
Получим зависимость
Распишем первое уравнение полученной системы, используя формулу двойного угла (
Заменим
Итак, координаты
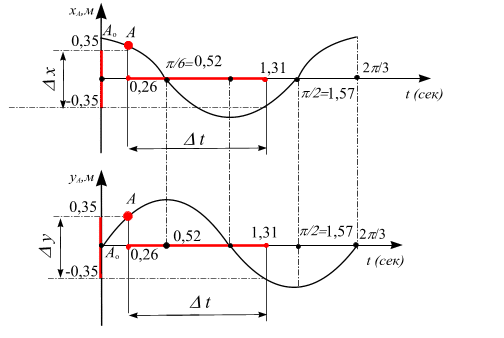
Построим график полученной функции. Вершина параболы находится в точке При В целом точка М совершает колебательные движения по параболе в ограниченной пунктиром области. Направление движения в первые 2 сек указано стрелкой на рис. 5.10. Пример 5.5. Точка движется в плоскости
где Требуетсяпостроить траекторию движения точки в декартовой системе координат. Решение. Построим траекторию движения точки.Дляэтого в декартовой системе координат определим область, в которой движется точка, т.е. область значений
Получим уравнение траектории в системе координат
Распишем первое уравнение системы (б), используя формулу двойного угла (
Получим:
Уравнение траектории в системе координат
Траекторией точки является парабола, вершина которой имеем координаты Проведем анализдвижения точки
Положения точки в разные моменты времени приведены в таблице 5.3. Таблица 5.3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.200 (0.013 с.) |

 . (а)
. (а)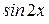 на
на  и
и 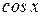 :
: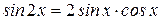 .
. .
.
 .
.
 Имеем:
Имеем: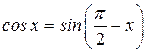 , тогда
, тогда
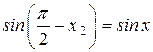 .
.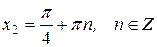 .
.
 . (б)
. (б) на
на 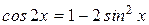 .
.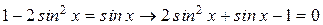 .
.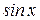 . Введем обозначения:
. Введем обозначения:  , тогда заданное уравнение сведется к квадратичному уравнению:
, тогда заданное уравнение сведется к квадратичному уравнению: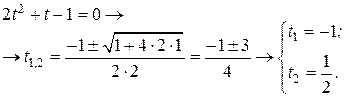
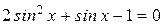 возможно лишь тогда, когда
возможно лишь тогда, когда  или
или  .
.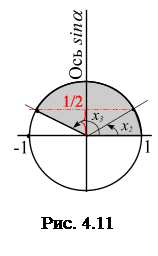 Первое уравнение:
Первое уравнение: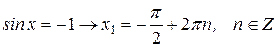 .
.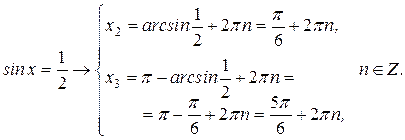
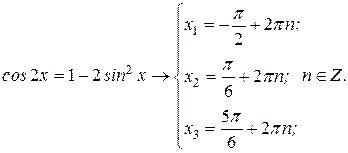
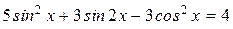 . (в)
. (в) .
.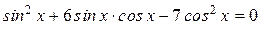 .
.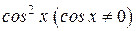 , получим
, получим . (г)
. (г) .
. , тогда уравнение (г) будет иметь вид
, тогда уравнение (г) будет иметь вид
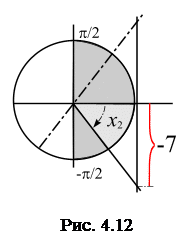 Решим полученные простейшие тригонометрические уравнения (рис. 4.12).
Решим полученные простейшие тригонометрические уравнения (рис. 4.12).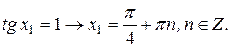
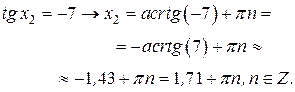
 .
.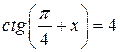 .
.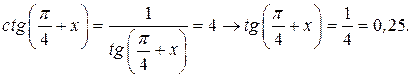


 . (а)
. (а)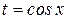 , тогда уравнение (а) будет иметь вид
, тогда уравнение (а) будет иметь вид

 .
.
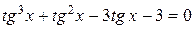 .
. ,
, 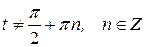 .
.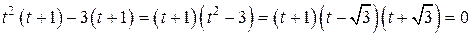 ,
,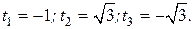
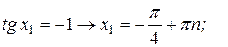

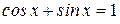 . (а)
. (а)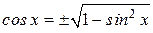 , тогда уравнение (а) примет вид
, тогда уравнение (а) примет вид .
.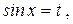 получим
получим
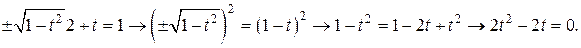
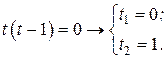
 удовлетворяет уравнению (а) при
удовлетворяет уравнению (а) при 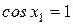 , следовательно, для решения
, следовательно, для решения 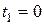 следует взять знак
следует взять знак 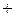 перед радикалом.
перед радикалом.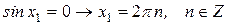 .
.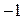 .
. .
.
 (время).
(время). декартовой системы координат, следовательно, координата
декартовой системы координат, следовательно, координата  должна зависеть от
должна зависеть от 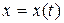 . Если периодические движения проходит в плоскости
. Если периодические движения проходит в плоскости 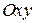 декартовой системы координат, тогда задаются две функции:
декартовой системы координат, тогда задаются две функции: 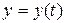 .
. в выбранной системе координат евклидового пространства называется траекторией движущейся точки. Если в интервале времени
в выбранной системе координат евклидового пространства называется траекторией движущейся точки. Если в интервале времени  движется по оси
движется по оси 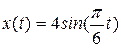 . (а)
. (а)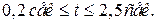
 , тогда уравнение (а) будет иметь вид
, тогда уравнение (а) будет иметь вид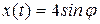 .
.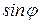 ограничена, т.е.
ограничена, т.е. 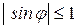 , следовательно
, следовательно .
.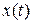 определена в пределах (рис. 5.1, а)
определена в пределах (рис. 5.1, а)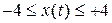 .
.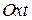 , здесь
, здесь  , рис.5.1,а. Графиком этой функции является синусоида,
, рис.5.1,а. Графиком этой функции является синусоида,  . При
. При 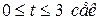 функция
функция 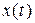 возрастает до
возрастает до 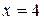 , далее при
, далее при 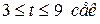 функция убывает до
функция убывает до 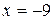 , при
, при 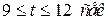 функция возрастает до
функция возрастает до  . Период функции
. Период функции 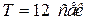 .
. , который и является траекторией движения точки
, который и является траекторией движения точки 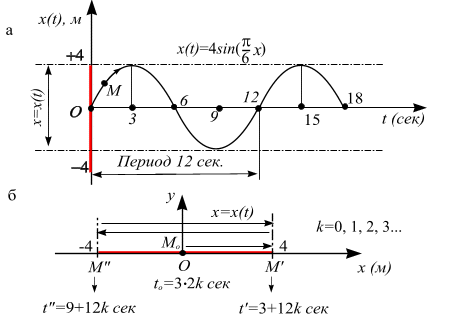
 точка
точка  начинает движение вправо из положения
начинает движение вправо из положения 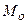
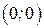 .
.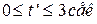 точка
точка 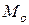 движется вправо, проходит
движется вправо, проходит  до точки
до точки  и останавливается.
и останавливается. начинает движение влево, проходя положение
начинает движение влево, проходя положение  , и останавливается в точке
, и останавливается в точке 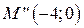 .
. точка движется вправо и т. д. Движение повторяется до бесконечности.
точка движется вправо и т. д. Движение повторяется до бесконечности. точка
точка  Нетрудно видеть (рис. 5.1, а), что при
Нетрудно видеть (рис. 5.1, а), что при  где
где 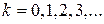 точка будет находиться в положении
точка будет находиться в положении  , при
, при 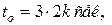 точка будет занимать положение
точка будет занимать положение  , при
, при  –
–  .
.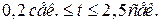
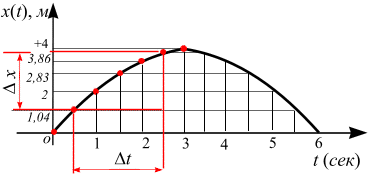 Рис. 5.2
Рис. 5.2
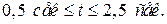
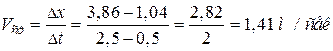 .
. 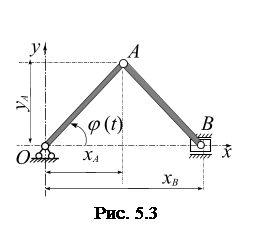 Пример 5.2. Положение кривошипа ОА в кривошипно-ползунном механизме (рис. 4.3) определяется углом
Пример 5.2. Положение кривошипа ОА в кривошипно-ползунном механизме (рис. 4.3) определяется углом 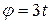 (рад). Определить траекторию движения точек
(рад). Определить траекторию движения точек  и
и  и вычислить среднюю скорость точки
и вычислить среднюю скорость точки  , если
, если  м.
м.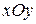 совместим с точкой О кривошипа 0А (рис. 5.3).Движение каждой точки данного механизма можно задать координатным способом относительно выбранной системы отсчета, т.е. задать координаты
совместим с точкой О кривошипа 0А (рис. 5.3).Движение каждой точки данного механизма можно задать координатным способом относительно выбранной системы отсчета, т.е. задать координаты 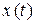 и
и 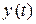 каждой точки.
каждой точки.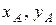 :
: (а)
(а) Дляпостроения траектории в декартовой системе координат евклидового пространства определим область значений
Дляпостроения траектории в декартовой системе координат евклидового пространства определим область значений  и
и  . Функции
. Функции  и
и  ограничены, тогда область значений
ограничены, тогда область значений  и
и 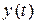 определяется неравенствами:
определяется неравенствами: (б)
(б)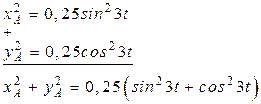
 , получим:
, получим: .
.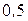 м.
м.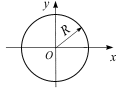 Справка. Каноническое уравнение окружности радиусом
Справка. Каноническое уравнение окружности радиусом  имеет вид
имеет вид 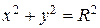 .
.
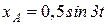 и
и 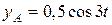 в системах координат
в системах координат 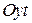 , соответственно (рис. 5.5). Здесь
, соответственно (рис. 5.5). Здесь 
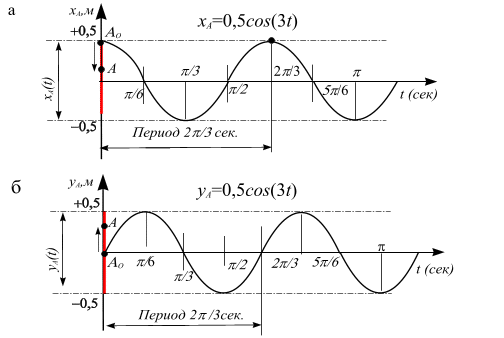
 при имеет координаты
при имеет координаты  .
. функция
функция  возрастает, следовательно, точка от положения
возрастает, следовательно, точка от положения 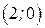 начинает движение по окружности против часовой стрелки (рис. 5.4). Период движения
начинает движение по окружности против часовой стрелки (рис. 5.4). Период движения 
 .
.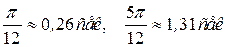 .
.
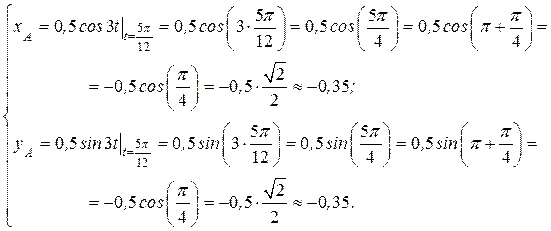
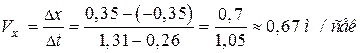 ,
,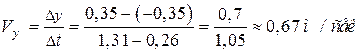 ,
,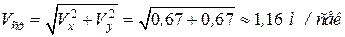 .
.  (рис. 5.7, а):
(рис. 5.7, а):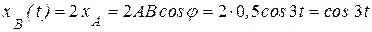 .
. определим область значений
определим область значений  . Функция
. Функция 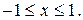 (б)
(б) , рис. 5.7, а.
, рис. 5.7, а.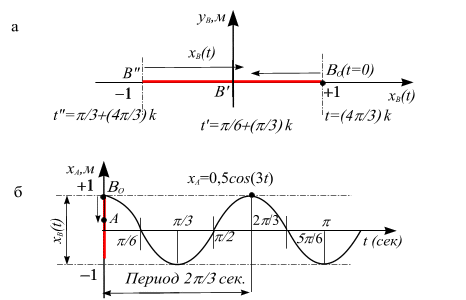
 , рис. 5.7, б. Далее точка движется влево и за
, рис. 5.7, б. Далее точка движется влево и за 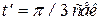 проходит положение
проходит положение 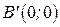 и достигает положение
и достигает положение  , далее возвращается в положение
, далее возвращается в положение 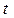 , сек
, сек
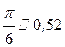
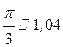
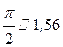

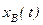


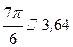
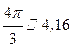
 сек, следовательно, период движения
сек, следовательно, период движения  , что составляет
, что составляет 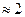 сек.
сек. точка
точка  ;
; где
где 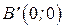 ;
; где
где 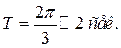
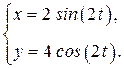 (а)
(а) в промежутке времени
в промежутке времени 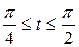 .
. является синусоида с периодом
является синусоида с периодом  сек и
сек и 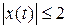 , рис. 5.8, а.
, рис. 5.8, а.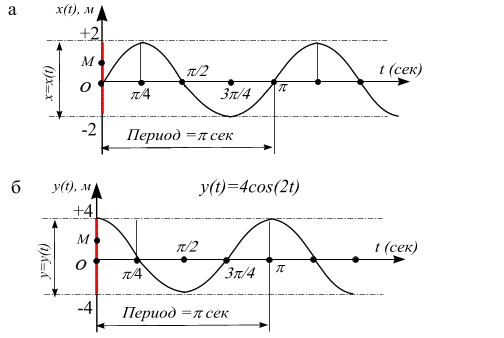
 :
: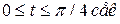 функция
функция 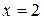 ;
; функция убывает от
функция убывает от 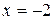 ;
;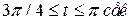 функция возрастает от
функция возрастает от 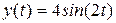 является косинусоида с периодом
является косинусоида с периодом  (рис. 5.8, б).
(рис. 5.8, б). :
: функция
функция 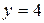 до
до 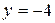 ;
; – при
– при  функция возрастает опять до
функция возрастает опять до 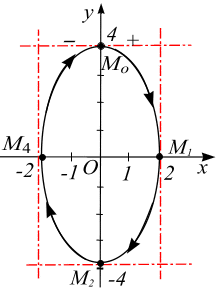 Точка движется в евклидовом пространстве
Точка движется в евклидовом пространстве  и
и 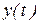 .
.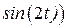 и
и 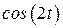 - ограничены, т.е.
- ограничены, т.е.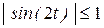 ,
, 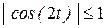 ,
,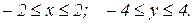
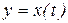 , которая является траекторией точки в евклидовом пространстве
, которая является траекторией точки в евклидовом пространстве 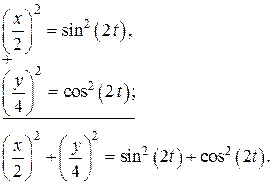
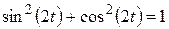 , получим:
, получим: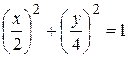 . (б)
. (б)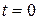 , находим положение точки
, находим положение точки 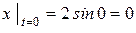 ;
;  см.
см.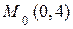 . Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией
. Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией 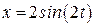 и убывающей функцией
и убывающей функцией 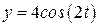 , поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка движется по эллипсу по часовой стрелке с периодом
, поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка движется по эллипсу по часовой стрелке с периодом 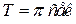 .
. ,
,
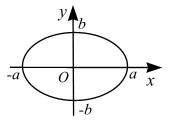 где а – полуось эллипса на оси
где а – полуось эллипса на оси  – полуось эллипса на оси
– полуось эллипса на оси 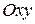 задано координатным способом уравнения
задано координатным способом уравнения 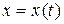 ,
,  :
:
 выражены в см,
выражены в см, 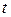 - в сек.
- в сек. сек.
сек.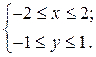 (в)
(в) . Для этого из (а) и (б) исключим параметр
. Для этого из (а) и (б) исключим параметр 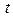 . Введём обозначение
. Введём обозначение 
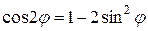 ), и приведем подобные члены:
), и приведем подобные члены:
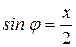 , получим
, получим .
.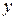 декартовой системы координат
декартовой системы координат 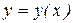 . Эта зависимость определяет траекторию движения точки в евклидовом пространстве, ограниченной системой неравенств (в). Итак, получили, что точка
. Эта зависимость определяет траекторию движения точки в евклидовом пространстве, ограниченной системой неравенств (в). Итак, получили, что точка 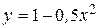 , где
, где 
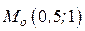 , ветви параболы вытянуты вдоль оси
, ветви параболы вытянуты вдоль оси 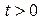 функция
функция  убывает, следовательно, точка из положения
убывает, следовательно, точка из положения 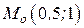 начинает движение по правой ветви параболы до точки
начинает движение по правой ветви параболы до точки 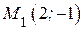 , далее точка движется обратно по верхней ветви параболы и через точку с координатами
, далее точка движется обратно по верхней ветви параболы и через точку с координатами 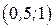 движется по нижней ветви параболы до точки
движется по нижней ветви параболы до точки 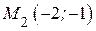 и т.д.
и т.д.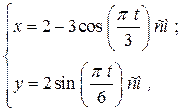 (а)
(а)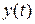 . Функции
. Функции  - ограничены, т.е.
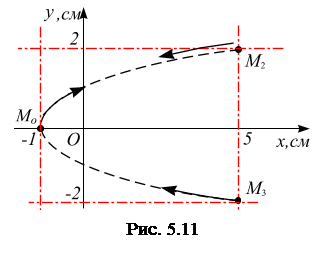
- ограничены, т.е.  , получаем из (а), рис. 5.11:
, получаем из (а), рис. 5.11:
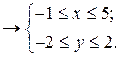
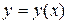 . Для этого из уравнений (а) исключим параметр
. Для этого из уравнений (а) исключим параметр 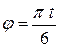 , тогда уравнения (а) перепишутся в виде
, тогда уравнения (а) перепишутся в виде (б)
(б)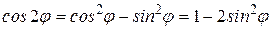 ),
),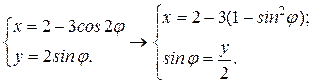

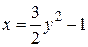 , где
, где  . (с)
. (с)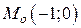 ; ветви параболы вытянуты вдоль оси
; ветви параболы вытянуты вдоль оси 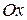 (рис. 5.11).
(рис. 5.11).