
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий случай тригонометрических уравнений
Рассмотрим уравнение вида
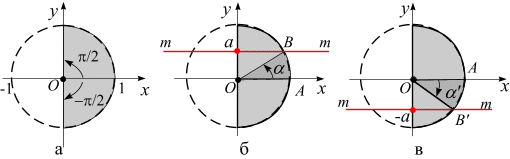
при различных значениях а. Для наглядности изобразим тригонометрические окружности, рис. 4.5.
Рис. 4.5
Точкам пересечения прямой « Случай 1. Пусть Случай 2. Пусть
Случай 3. Пусть
Случай 4. Пусть
4.3. Понятие арксинуса, арккосинуса, арктангенса и арктангенса числа
I. Для записи одного из корней уравнения
Для изображения угла С использованием арксинуса при
Рис. 4.6 В таблице 4.5 приведены значения Таблица 4.5
Числовое значение
Таблица 4.6
II. Для записи одного из корней уравнения
Для изображения угла
Числовое значение Таблица 4.7
Для уравнения
Таблица 4.8
III. Для записи одного из корней уравнения
Корни уравнения
В таблице 4.9 приведены значения Таблица 4.9
Пример. Решить уравнение Решение. Для уравнения
Таблица 4.10
IV. Решение уравнения Пример. Решить уравнение Решение. Данное уравнение равносильно уравнению
Имеем
В таблице 4.9 числовое значение Числовое значение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.248 (0.017 с.) |


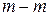 » с окружностью соответствуют все направленные углы, косинус которых равен а. В зависимости от значения а, возможны несколько случаев.
» с окружностью соответствуют все направленные углы, косинус которых равен а. В зависимости от значения а, возможны несколько случаев. . Тогда прямая «
. Тогда прямая «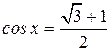 не имеет решений, так как
не имеет решений, так как  .
. (рис. 4.5, б). Тогда прямая «
(рис. 4.5, б). Тогда прямая « . Все направленные углы, которые соответствуют точке
. Все направленные углы, которые соответствуют точке  , можно записать в виде
, можно записать в виде ,
,  .
. (рис. 4.5, в). Тогда прямая «
(рис. 4.5, в). Тогда прямая « . Все направленные углы, которые соответствуют точке
. Все направленные углы, которые соответствуют точке  , можно записать в виде
, можно записать в виде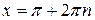 ,
, 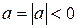 (рис. 4.5, д), например
(рис. 4.5, д), например  . Тогда прямая «
. Тогда прямая « и
и  . Если известен один корень уравнения
. Если известен один корень уравнения  (
( ), то все остальные корни можно найти точно так же, как это сделано в пункте II предыдущего параграфа, то есть
), то все остальные корни можно найти точно так же, как это сделано в пункте II предыдущего параграфа, то есть ,
,  для записи корней тригонометрических уравнений
для записи корней тригонометрических уравнений вводятся новое понятие и обозначение.
вводятся новое понятие и обозначение. арксинусом числа а называется угол
арксинусом числа а называется угол  (в радианах) из промежутка
(в радианах) из промежутка 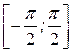 , для которого
, для которого  . Арксинус числа
. Арксинус числа  .
.
 точку с ординатой
точку с ординатой  , на рис 4.6, в –
, на рис 4.6, в –  .
.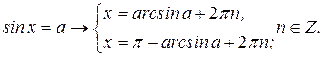














 для любого числа
для любого числа  по общим формулам можно сразу записать ответ (числовые значения
по общим формулам можно сразу записать ответ (числовые значения 
 , для которого
, для которого 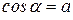 . Арккосинус числа
. Арккосинус числа  .
.
 точку с ординатой
точку с ординатой  С использованием арккосинуса при
С использованием арккосинуса при  В таблице 4.7 приведены значения
В таблице 4.7 приведены значения 



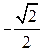
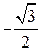




 по общим формулам можно сразу записать ответ (числовые значения
по общим формулам можно сразу записать ответ (числовые значения 
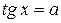 также вводятся понятие и обозначение.
также вводятся понятие и обозначение. . Арктангенс числа
. Арктангенс числа  .
.




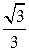

 Корни уравнения
Корни уравнения  при любом значении числа
при любом значении числа 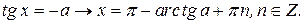
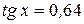 .
.
 при
при  сводится к решению уравнения вида
сводится к решению уравнения вида  (
( ).
). .
.

 .
. для любого числа
для любого числа 


