Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аргумент тригонометрической функцииСодержание книги Поиск на нашем сайте
Соответствие между углами и значениями данной тригонометрической функции позволяет всякую тригонометрическую функцию рассматривать как функцию; значениями аргумента являются углы, а значениями – числа. Если известна сторона Впишем в единичную окружность равносторонний треугольник
Имеем:
Итак, получили, что
Впишем в единичную окружность шестиугольник так, чтобы начальный радиус, лежащий на оси Имеем
Значения тригонометрических функций для некоторых аргументов приведены в таблице 1.3. Таблица 1.3
Приведенные значения тригонометрических функций полезно запомнить. Историческая справка. Значительный вклад в становление теории тригонометрических функций внесли арабские ученые. Достижением арабских ученых является то, что они отделили тригонометрию от астрономии. В первом тысячелетии н.э. происходит бурный расцвет культуры и науки в странах Арабского Халифата, и основные открытия тригонометрии принадлежат ученым этих стран.
Косинус – это сокращение латинского выражения “completely sinus”, т.е. дополнительный синус (или иначе - синус дополнительной дуги).
Туркменский ученый аль-Маразви первым из известных нам исследователей ввел понятие тригонометрических функций как отношение сторон прямоугольного треугольника (рис. 1.18) и составил таблицы синусов, тангенсов и котангенсов:
Значительных высот достигла тригонометрия и у индийских средневековых астрономов, достижением которых стала замена хорд синусами, что позволило вводить различные функции. В Индии было положено начало тригонометрии как учению о тригонометрических величинах.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.139 (0.008 с.) |

 правильного
правильного  -угольника, вписанного в тригонометрический круг (круг единичного радиуса), то легко вычислить значения тригонометрических функций от угла.
-угольника, вписанного в тригонометрический круг (круг единичного радиуса), то легко вычислить значения тригонометрических функций от угла. так, чтобы начальный радиус, лежащий на оси
так, чтобы начальный радиус, лежащий на оси  , поделил основание вписанного треугольника пополам (рис. 1.14). Тогда
, поделил основание вписанного треугольника пополам (рис. 1.14). Тогда  – синус угла
– синус угла  ,
, 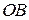 – косинус угла
– косинус угла  . Из геометрии известно, что катет, лежащий против угла в
. Из геометрии известно, что катет, лежащий против угла в  , равен половине гипотенузы.
, равен половине гипотенузы. Имеем
Имеем
 ;
;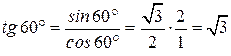 ;
; .
. Впишем в единичную окружность квадрат так, чтобы начальный радиус, лежащий на оси
Впишем в единичную окружность квадрат так, чтобы начальный радиус, лежащий на оси  ,
, 
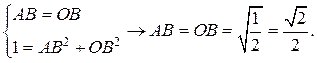
 ,
, ,
,  .
. . Из геометрии известно, что катет, лежащий против угла в
. Из геометрии известно, что катет, лежащий против угла в 
 .
. ,
, .
. , рис. 1.16’.
, рис. 1.16’.
 Рис. 1.16’
Рис. 1.16’
 будет соответствовать синусу угла
будет соответствовать синусу угла  , а
, а  – его косинусу, т.е.
– его косинусу, т.е.


 (градус)
(градус)


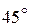













 Описывая положение звезд, ученые этих стран в 4-5 в. пользовались лучом (длина луча соответствовала 1 масштабу), который направляли на звезду. В трудах по астрономии индийского учёного Ариабхаты отрезок CB (рис. 1.17) назван “ардхаджива” (“ардха” – половина, “джива” – тетива лука, которая напоминает хорду). При переводе арабских математических текстов слово “ардхаджива” было заменено латинским словом “синус” (sinus – изгиб, кривизна).
Описывая положение звезд, ученые этих стран в 4-5 в. пользовались лучом (длина луча соответствовала 1 масштабу), который направляли на звезду. В трудах по астрономии индийского учёного Ариабхаты отрезок CB (рис. 1.17) назван “ардхаджива” (“ардха” – половина, “джива” – тетива лука, которая напоминает хорду). При переводе арабских математических текстов слово “ардхаджива” было заменено латинским словом “синус” (sinus – изгиб, кривизна).