
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы тригонометрии
Теорема синусов
В плоском треугольнике со сторонами
Доказательство. Рассмотрим
Длину стороны BD вычислим как разность AB и AD:
Вычислим по теореме Пифагора высоту Имеем
Подставим в последнее выражение вычисленные значения (а) и (б), получим
Раскроим скобки и приведем подобные члены, получим
Теорема доказана.
Решение. По теореме косинусов
Здесь по теореме приведения
Полезно эту задачу решить геометрически, т.е. построить заданный треугольник в масштабе и измерить сторону
Решение. Опустим из вершины
По теореме косинусов
или
Отсюда имеем:
Теорема синусов Рассмотрим
Доказательство. Рассмотрим произвольный треугольник, вписанный в окружность, обозначим его как ABC (рис. 2.4). Для доказательства всей теоремы, поскольку размеры треугольника выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R, например,
Из Повторив то же рассуждение для двух других сторон треугольника, получаем:
Если точки A и D лежат по разные стороны от прямой BC (рис. 2.5), то угол CDB равен углу Теорема сложения для косинуса. При произвольных значениях
Доказательство. Пусть точки
Вычислим квадрат расстояния между точками
Рассмотрим разность дуг Запишем координаты точки
Вычислим квадрат расстояния между точками
Приравняем правые части уравнений (1) и (2) между собой, получим
откуда
Заменив
Теорема доказана. Следствие 1. Подставляя в (4)
Эта формула позволяет 1. Заменить выражение 2. Разложить 3. Заменить выражение Следствие 1. Используя основное тригонометрическое тождество
Получим другие варианты формулы двойного угла
Пример 2.3. Вычислить Решение. Представим угол
Пример 2.4. Чему равно значение Решение. Воспользуемся формулой (3), получим
Формулы приведения Теорема сложения для синуса. При произвольных значениях
Доказательство. Синус угла
Заменив
Следствие. Если углы
Пример 2.5. Вычислить Решение.
Пример 2.6*. Вычислить Решение. Имеем:
Получили, что Пример 2.7*. Вычислить Решение. Имеем:
Получили, что Функции суммы и разности углов сведем в одну таблицу 2.1 Таблица 2.1
Рассмотрим формулы:
1. При
2. При
3. При
4. При
Значимые формулы приведения можно свести в одну таблицу 2.2. Таблица 2.2
Рассмотрим формулы:
1. При
2. При
3. При
4. При
Значимые формулы приведения можно свести в одну таблицу 2.3. Таблица 2.3
Эмпирические правила. Формул приведения много. Любую формулу приведения можно получить, зная значения тригонометрических функций в первой четверти, т. е. для углов
Правило 1. Перед приведенной функцией ставится тот знак, который имеет исходная функция в заданной четверти (квадранте), рис. 2.8. Правило 2. Для углов ( Правила приведения позволяют безошибочно и легко воспроизводить нужную формулу приведения. Все формулы приведения можно свести в одну таблицу 2.4. В практике удобно пользоваться два приведенных эмпирических правила, для этого их следует запомнить. Таблица 2.4
Пример 2.8. Вычислить Решение. 1.Угол
Имеем:
2. Угол Представим Имеем:
Представим
4. Представим угол
Угол Представим
5. Представим Тогда Пример 2.9. Вычислить Решение.
Представим
2. Угол Представим Имеем:
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.251.22 (0.104 с.) |

 и углом
и углом  , противолежащим стороне
, противолежащим стороне  (рис. 2.1), квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними, т. е. справедливо равенство
(рис. 2.1), квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними, т. е. справедливо равенство .
. . Из вершины C на сторону AB опустим высоту CD. Треугольник ADC является прямоугольным, поэтому величину стороны AD можно вычислить из соотношения тригонометрических функций:
. Из вершины C на сторону AB опустим высоту CD. Треугольник ADC является прямоугольным, поэтому величину стороны AD можно вычислить из соотношения тригонометрических функций: . (а)
. (а) . (б)
. (б) .
.
 .
.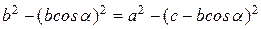 .
. ,
, . (1)
. (1) Пример 2.1. В треугольнике
Пример 2.1. В треугольнике  вычислить величину стороны
вычислить величину стороны  , если
, если  ,
,  , угол между сторонами равен
, угол между сторонами равен  (рис. 2.2).
(рис. 2.2).

 .
. Пример 2.2. Вычислить площадь треугольника
Пример 2.2. Вычислить площадь треугольника  ;
;  ;
;  (рис. 2.3).
(рис. 2.3). на основание
на основание  высоту
высоту  . Площадь треугольника
. Площадь треугольника  .
.
 .
. ;
; ;
;  .
.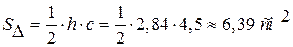 .
. , описанный вокруг треугольника окружности радиуса
, описанный вокруг треугольника окружности радиуса  ; a, b, c – стороны треугольника; α, β, γ – величины противолежащих этим сторонам углов (рис. 2.4).
; a, b, c – стороны треугольника; α, β, γ – величины противолежащих этим сторонам углов (рис. 2.4). Теорема. Стороны треугольника ABC пропорциональны синусам противолежащих углов:
Теорема. Стороны треугольника ABC пропорциональны синусам противолежащих углов: ,
,  .
. Проведем диаметр BD для описанной окружности (рис. 2.5). Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность). Рассмотрим случай, когда точки A и D лежат по одну сторону от прямой BC. Изгеометрии известно, что углы, вписанные в окружность и опирающиеся на одну и ту же дугу, равны между собой. Тогда угол
Проведем диаметр BD для описанной окружности (рис. 2.5). Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность). Рассмотрим случай, когда точки A и D лежат по одну сторону от прямой BC. Изгеометрии известно, что углы, вписанные в окружность и опирающиеся на одну и ту же дугу, равны между собой. Тогда угол 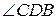 равен углу
равен углу  .
.

 .
. . Поскольку
. Поскольку  , то указанные варианты построения треугольника все равно приведут к одному результату.
, то указанные варианты построения треугольника все равно приведут к одному результату. имеют место теоремы сложения:
имеют место теоремы сложения: ;
;
 .
. и
и  – точки единичной окружности (рис. 2.6). Запишем координаты точек
– точки единичной окружности (рис. 2.6). Запишем координаты точек 
 (1)
(1) , измеряющаяся числом
, измеряющаяся числом 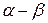 . Отложим È
. Отложим È  . Пусть
. Пусть  – конец отложенной, т.е. дуги È
– конец отложенной, т.е. дуги È 
 (2)
(2) ,
, в формуле (3), получим
в формуле (3), получим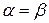 , получим формулу косинуса двойного угла:
, получим формулу косинуса двойного угла: .
. тождественно равным ему выражением
тождественно равным ему выражением  , зависящим от
, зависящим от  и
и  .
. :
:

 .
. в виде разности
в виде разности  . Тогда
. Тогда
 ?
?


 .
. равен косинусу аргумента
равен косинусу аргумента  , т.е.
, т.е.  , рис. 2.7. Этот аргумент можно представить следующим образом
, рис. 2.7. Этот аргумент можно представить следующим образом
 Тогда
Тогда (5)
(5)
 .
. ,
,  ,
,  ,
,  .
.

















 . Тогда:
. Тогда: ;
; .
. . Тогда:
. Тогда: ;
; .
. . Тогда:
. Тогда:

 . Тогда:
. Тогда: ;
; .
. ;
; 
 ;
;  .
.
 ;
;
 ;
; .
. ;
; .
. ;
; .
. .
.
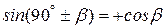 ;
; 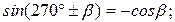
 ;
;  .
.
 (значения тригонометрических функций в смысле главного значения) и зная знак тригонометрической функции в различных четвертях (квадрантах), рис. 2.8. Анализируя вывод формул приведения, приведенных в таблицах 2.1–2.2, можно сформулировать общие два эмпирических правила, которыми следует пользоваться для использования этих формул без их запоминания.
(значения тригонометрических функций в смысле главного значения) и зная знак тригонометрической функции в различных четвертях (квадрантах), рис. 2.8. Анализируя вывод формул приведения, приведенных в таблицах 2.1–2.2, можно сформулировать общие два эмпирических правила, которыми следует пользоваться для использования этих формул без их запоминания. Рис. 2.8
Рис. 2.8  ) или (
) или ( ), образованных откладыванием угла
), образованных откладыванием угла  от оси абсцисс (оси
от оси абсцисс (оси  ), формула приведения название функции не измененяет. Для углов (
), формула приведения название функции не измененяет. Для углов ( ) или (
) или ( ), образованных откладыванием угла
), образованных откладыванием угла  ), формула приведения название функции измененяет: синус переходит в косинус (
), формула приведения название функции измененяет: синус переходит в косинус ( ), косинус переходит в синус (
), косинус переходит в синус ( ), тангенс переходит в котангенс (
), тангенс переходит в котангенс ( ), котангенс переходит в тангенс (
), котангенс переходит в тангенс ( ).
). 









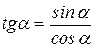



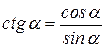




 ,
,  ,
,  ,
,  ,
,  .
. Представим
Представим  , имеем дело со случаем
, имеем дело со случаем  , следовательно, меняем функцию с синуса на косинус.
, следовательно, меняем функцию с синуса на косинус.
 находится в третьей четверти
находится в третьей четверти  , имеем дело со случаем
, имеем дело со случаем 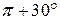 , следовательно, функция не меняется.
, следовательно, функция не меняется.
 3. Угол
3. Угол  находится в четвертой четверти (рис. 2.11), из рисунка видно, что знак
находится в четвертой четверти (рис. 2.11), из рисунка видно, что знак  в этой четверти равен «+», значит у приведенной функции тоже будет знак «+».
в этой четверти равен «+», значит у приведенной функции тоже будет знак «+». , имеем дело со случаем
, имеем дело со случаем  , следовательно, меняем функцию с косинуса на синус.
, следовательно, меняем функцию с косинуса на синус. Имеем:
Имеем:
 , тогда (рис. 2.12):
, тогда (рис. 2.12):
 находится во второй четверти; из рисунка видно, что знак
находится во второй четверти; из рисунка видно, что знак  , имеем дело со случаем
, имеем дело со случаем  Имеем:
Имеем: 
 как сумму
как сумму  (рис. 2.13).
(рис. 2.13).
 ,
,  .
. 1. Угол
1. Угол  в этой четверти «–», значит у приведенной функции тоже будет знак «–».
в этой четверти «–», значит у приведенной функции тоже будет знак «–». .
. Имеем:
Имеем:




