
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прикладные аспекты основных теорем тригонометрии
Задача 1. Даны три стороны треугольника Противолежащие углы
Аналогично вычисляются косинус угла Пример 2.10. Задано: Решение. Применим теорему косинусов для квадрата стороны, лежащей против угла
Тогда
Сторону
Далее, косинус угла
Угол
Пример 2.11. Задано: Решение. По теореме косинусов имеем:
Далее
Вычислим
Итак,
Задача 3. Заданы:сторона
Пример 2.12. Вычислить стороны Решение. По теореме синусов имеем
Задача 4. Заданы:сторона Первый шаг – вычисляем угол
Тогда
Используя теорему синусов, получим:
Если Пример 2.13. Дано: Решение. Вычислим угол
Имеем:
Используя теорему синусов, получим:
Из теоремы синусов запишем равенство
Выражение I. Если II. Если
III. Если
Далее вычислить
При Пример 2.14. Задано:
Решение. Из теоремы синусов запишем равенство
Откуда
Вычислим угол
Сторону
Пример 2.15. Задано: Решение. Из теоремы синусов запишем равенство
Задача решения не имеет. Смешанные задачи
Решение. Пусть ABCD – параллелограмм, рис. 2.21. Обозначим стороны Применим теорему косинусов к треугольникам
Сложим эти равенства между собой
Решение. Рассмотрим треугольник Для треугольника
Преобразуем выражение, стоящее в скобках:
Подставим полученное выражение в (а), получим
Как следствие рассмотренной задачи, получим теорему синусов. Рассмотрим вписанный треугольник Из предыдущих расчетов получаем:
В результате получаем теорему синусов: во всяком треугольнике стороны Итак
Теорема. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Доказательство. Пусть
Затем применим теорему синусов для треугольника
Так как
Разделим правые и левые части выражений (а) и (б) между собой, получим
Итак, получили, что Пример 2.18. В равнобедренный треугольник, основание которого равно Решение. Пусть
Из прямоугольного
Если
Из
Пример 2.19. Вычислить радиус вписанной окружности в Решение. Пусть Из условия
Пусть
Из
Основные тригонометрические определения, теоремы и формулы, которые следует запомнить.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.63.90 (0.045 с.) |
 Основные задачи на решение треугольников. Рассмотрим произвольный
Основные задачи на решение треугольников. Рассмотрим произвольный  , со сторонами
, со сторонами  и противолежащими углами
и противолежащими углами 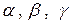 (рис. 2.16). Основные задачи на решение треугольников состоят в вычислении по некоторым известным элементам треугольника остальных элементов треугольника. Рассмотрим основные задачи.
(рис. 2.16). Основные задачи на решение треугольников состоят в вычислении по некоторым известным элементам треугольника остальных элементов треугольника. Рассмотрим основные задачи.
 и
и  .
. Вычислить
Вычислить  .
. , и подставим известные значения (рис. 2.16):
, и подставим известные значения (рис. 2.16):


 Задача 2. Заданы в треугольнике
Задача 2. Заданы в треугольнике  две стороны
две стороны  и угол между ними
и угол между ними  и углы
и углы 
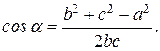
 .
. . Вычислить
. Вычислить  .
.
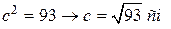 .
.



 и три угла
и три угла 
 . Для решения поставленной задачи используем теорему синусов:
. Для решения поставленной задачи используем теорему синусов: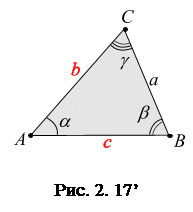

 треугольника
треугольника  ;
; 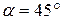 ;
;  ;
;  (рис.2.17’).
(рис.2.17’).
 .
. ,
,

 , то задача имеет единственное решение.
, то задача имеет единственное решение.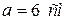 ;
;  .
. .
. .
.
 Задача
Задача  . Заданы две стороны и угол, лежащий против одной их них, например, сторона
. Заданы две стороны и угол, лежащий против одной их них, например, сторона  .
. может принимать различные значения.
может принимать различные значения. , то задача не имеет решения.
, то задача не имеет решения. , тогда
, тогда  , а это значит, что
, а это значит, что  . Следовательно, возможен только прямоугольный треугольник, рис. 2.18, б. Тогда сторона
. Следовательно, возможен только прямоугольный треугольник, рис. 2.18, б. Тогда сторона  .
. , тогда
, тогда 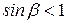 . В этом случае угол
. В этом случае угол  можно вычислить угол
можно вычислить угол 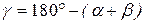 .
. , а затем из теоремы синусов вычислить
, а затем из теоремы синусов вычислить 
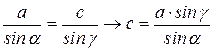 .
. задача иметь решения не будет.
задача иметь решения не будет.
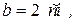



 .
.
 .
.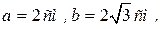 ,
,  , рис. 2.20. Вычислить
, рис. 2.20. Вычислить 
 Пример 2.16. Показать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Пример 2.16. Показать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.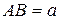 ,
,  , а угол при вершине
, а угол при вершине  обозначим
обозначим  будет равен
будет равен  .
. и
и  , получим
, получим (1) Отметим, что
(1) Отметим, что  . Тогда (1) примет вид
. Тогда (1) примет вид

 Пример 2.17. Вычислить длину хорды
Пример 2.17. Вычислить длину хорды  , если задан угол
, если задан угол  , (рис. 2.22).
, (рис. 2.22). . По теореме об измерении угла, вписанного в окружность, центральный угол
. По теореме об измерении угла, вписанного в окружность, центральный угол  , опирающийся на дугу
, опирающийся на дугу  .
. . (а)
. (а)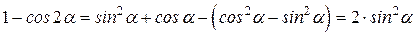 .
. .
. Итак,
Итак, .
. и углами
и углами 
 ,
, ,
,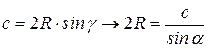 .
. .
.  – биссектриса треугольника
– биссектриса треугольника 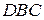 :
:
 . (а)
. (а) :
: .
. , то
, то . (в)
. (в)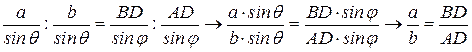 .
. , что и требовалось доказать.
, что и требовалось доказать. , вписана окружность, радиус которой равен
, вписана окружность, радиус которой равен  . Вычислить боковые стороны треугольника.
. Вычислить боковые стороны треугольника. – центр вписанной окружности. Тогда точка
– центр вписанной окружности. Тогда точка  треугольника
треугольника  ,
,  , тогда
, тогда 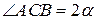 .
. получим:
получим:


 , имеем:
, имеем:
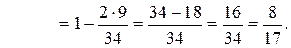
 имеем:
имеем: 
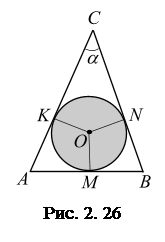

 равны радиусу вписанной окружности, проведенные в точки ее касания со сторонами треугольника.
равны радиусу вписанной окружности, проведенные в точки ее касания со сторонами треугольника. , получим:
, получим:
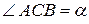 , тогда по теореме косинусов имеем:
, тогда по теореме косинусов имеем: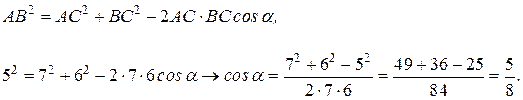



 .
.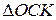 имеем
имеем



