
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Систематические погрешности, оценка их величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Физика. Лабораторный практикум Часть 1 Механика. Молекулярная физика И термодинамика Для студентов технологического, механико-радиотехнического, экономического факультетов и Института дистанционного и заочного обучения
шахты 2004 УДК 539.1(07) ББК 22.36я7 г Составители: доц. каф. «Физика», к.т.н. В.В. Глебов (№1) доц. каф. «Физика», к.ф-м.н. И.Н. Даниленко (№2) Зав. каф. «Физика», проф., д.т.н. С.В. Кирсанов (№3) ассистент каф. «Физика» А.В. Меркулова (№4) ассистент каф. «Физика» С.В. Токарева (№5) доц. каф. «Физика», к.ф-м.н. В.В. Коноваленко (№6) доц. каф. «Физика», к.ф-м.н. А.А. Баранников (№7) доц. каф. «Физика», к.т.н. Н.З. Алиева (№8) доц. каф. «Физика», к.т.н. Ю.В. Присяжнюк (№9) доц. каф. «Физика», к.т.н. Н.И. Санников (№10) Рецензент: доц. каф. «Радиотехника», к.ф-м.н. И.Н. Семенихин Г Глебов В.В. физика. Лабораторный практикум: В 3 ч. Ч.1: Механика. Молекулярная физика и термодинамика / В.В. Глебов, И.Н. Даниленко, В.В. Коноваленко, Н.З. Алиева, А.В. Меркулова, С.В. Кирсанов, С.В. Токарева, Н.И. Санников, Ю.В. Присяжнюк, А.А. Баранников; Под. ред. Ю.В. Присяжнюка. – Шахты: Изд-во ЮРГУЭС, 2004. – 79 с.
Лабораторный практикум издан в 3-х частях и предназначен для подготовки студентов технологического, механико-радиотехнического, экономического факультетов и Института дистанционного и заочного обучения к выполнению лабораторных работ по курсу «Физика». Первая часть охватывает такие разделы курса, как «Механика», «Молекулярная физика и термодинамика». В содержание каждой лабораторной работы входит: краткая теория, описания экспериментальной установки и методики проведения измерений, указания по обработки экспериментальных данных и представления полученных результатов.
УДК 539.1(07) ББК 22.36я7 © Южно-Российский государственный университет экономики и сервиса, 2004 © В.В. Глебов, И.Н. Даниленко, В.В. Коноваленко и др., 2004 СОДЕРЖАНИЕ Лабораторная работа №1: Измерение физических величин и математическая обработка результатов измерений. 4 Лабораторная работа №2: Определение ускорения силы тяжести при свободном падении тела. 17 Лабораторная работа №3: Определение ускорения свободного падения при помощи оборотного физического и математического маятников. 24 Лабораторная работа №4: Определение момента инерции твердого тела при помощи крутильного маятника. 34 Лабораторная работа №5: Определение момента инерции тел с помощью маятника Максвелла. 41 Лабораторная работа №6: Изучение законов вращательного движения с помощью маятника Обербека. 48 Лабораторная работа №7: Определение средней длинны свободного пробега и эффективного диаметра молекул воздуха. 57 Лабораторная работа №8: Определение коэффициента внутреннего трения жидкости методом падающего шарика (метод Стокса) 62 Лабораторная работа №9: Определение показателя адиабаты газа. 65 Лабораторная работа №10: Определение изменения энтропии. 74
Лабораторная работа №1: Измерение физических величин и математическая обработка результатов измерений Понятие об измерении Измерением называется нахождение значения физической величины опытным путем с помощью специальных технических средств. При измерении физическая величина сравнивается с некоторым ее значением, принятым за единицу. Результат измерения представляет собой, как правило, именованное число: числовое значение измеренной величины и наименование единицы. Например: напряжение U= 1,5 В; сила тока I = 0,27 А;частота n= 528 Гц. Погрешностью измерения физической величины называется отклонение результата измерения Xизм от истинного значения Xист D Х=Хизм -Хист Истинное значение физической величины не может быть известно, поэтому вместо него берут найденную экспериментально приближенную оценку истинного значения, которую затем используют вместо истинного для данной цели. Из указанного следует, что найденная при измерениях оценка истинного значения величины обязательно должна сопровождаться указанием ее погрешности. Поскольку погрешность определяет диапазон, внутрь которого истинное значение попадает только с некоторой вероятностью, то эта вероятность обязательно должна быть указана. Классификация измерений Прямые измерения – это измерения, при которых искомое значение величины U находится непосредственно из опытных данных Х. Например: измерение длины линейкой, напряжение вольтметром, силы тока амперметром. Математическая зависимость между измеряемыми и определяемыми путем прямых измерений величинами выражается так: U=Х. Эта связь называется уравнением измерения. Косвенные измерения – это измерения, при которых искомая величина находится с помощью заранее известной математической формулы. Причем аргументами этой формулы являются величины, определенные путем прямых измерений. Например: измерение объема куба V по измерению длины его ребра L: V=L 3 Уравнение косвенных измерений в общем случае имеет вид: Y = f (Х 1, Х 2, Х 3 ,... Хn), где Хj – аргументы, полученные путем прямых измерений, либо известные константы. Классификация погрешностей Классификация погрешностей по форме выражения Абсолютной погрешностью D называют погрешность, выраженную в единицах измерения величины. Например, D u = 0,5 В и т.п. D Х=Хизм - Хист Если измеренная величина превышает истинное значение, погрешность положительна, если же измеренная величина меньше истинного значения, то погрешность отрицательна. Величина абсолютной погрешности не характеризует качество измерения. Действительно, если полученная погрешность Относительной погрешностью d называется отношение абсолютной погрешности к истинному значению величины.
Эта погрешность является характеристикой качества измерения. Пример тот же - измерение длины стола L 1 и диаметра L 2 карандаша. Пусть L 1 = 1 м, а L 2 = 1 см = 0,01 м. Тогда относительные погрешности равны: для стола: для карандаша Видно, что относительная погрешность измерения длины стола в 100 раз меньше, чем диаметра карандаша, то есть качество измерения длины стола в 100 раз выше при одинаковой величине абсолютной погрешности. Классификация погрешностей по закономерности их появления Промахи – ошибки, возникающие в результате неправильных действий экспериментатора. Это может быть описка при записи, неправильное снятие показаний прибора и т.д. Обнаруженные промахи следует всегда исключать из рассмотрения при обработке результатов измерений. Систематическая погрешность D с – это составляющая общей погрешности измерения, которая остается постоянной при повторных измерениях одной и той же величины в одних и тех же условиях. К систематическим погрешностям относятся: погрешность градуировки шкалы прибора, температурная погрешность и т.д. Анализ источников систематических погрешностей – одна из основных задач при точных измерениях. Иногда найденная систематическая погрешность может быть исключена из результата измерения путем введения соответствующей поправки. Способы оценки систематической погрешности описаны ниже. Случайная погрешность D сл – это вторая составляющая общей погрешности измерения, которая при повторных измерениях в одних и тех же условиях изменяется случайным образом, без видимой закономерности. Случайные погрешности являются следствием наложения случайных процессов, сопровождающих любое физическое измерение и влияющих на его результат. Следует отметить, что случайная погрешность уменьшается при увеличении количества повторных измерений в отличие от систематической погрешности, которая не меняется. Способ оценки случайной погрешности описан ниже. Суммирование погрешностей Общая абсолютная погрешность измерения D всегда содержит две составляющие: систематическую погрешность D с и случайную погрешность D сл Можно оценить величину D с (п.4) и отдельно оценить величину D. Как после этого найти суммарную погрешность? Общая абсолютная погрешность находится по формуле
Сложение погрешностей можно интерпретировать и графически (рис. 1.2). Общая погрешность D равна гипотенузе треугольника, катетами которого являются Dс и Dсл. Покажем, что часто при сложении погрешностей формулой (1.3) можно и не пользоваться. Пусть одна из погрешностей, например Dс, в 2 раза меньше, чем другая Dсл. Тогда, согласно формуле (1.3),
Из сказанного вытекают следующие правила измерений: 1. Если систематическая погрешность в два и более раз больше, чем случайная, то случайной погрешностью можно пренебречь; большое количество измерений при этом проводить нецелесообразно, так как D с не уменьшается при увеличении n. Итак, если D с > 2Dсл, то D» D с (при этом достаточно провести три-четыре измерения только для того, чтобы убедиться, что показания прибора повторяются без случайных отклонений). 2. Если, наоборот, случайная погрешность более чем в 2 раза превышает систематическую, то систематической погрешностью можно пренебречь, то есть если D сл > 2D с, то D» D сл (желательно провести побольше измерений для уменьшения D сл). 3. Если обе составляющие общей абсолютной погрешности соизмеримы, то следует их суммировать по формуле (1.3) или графически по рис. 1.3. (Количество измерений целесообразно увеличить для уменьшения Dсл и перехода к случаю 1). Принимая во внимание, что вместо D сл можно взять её оценку s, то формула (1.3) примет вид:
На схеме (рис. 1.3) обобщены методы определения погрешности при прямых измерениях.
Правила округления погрешности и результата измерения Рассчитывая значения систематической, случайной и суммарной погрешностей, особенно при использовании электронного калькулятора, получают значение с большим числом знаков. Однако исходные данные для этих расчетов всегда указываются с одной или двумя значащими цифрами. Действительно, класс точности прибора на его шкале указывается не более чем с двумя значащими цифрами, а среднее квадратичное отклонение не имеет смысла записывать с более чем двумя значащими цифрами, так как точность этой оценки при 10 измерениях не выше 30%. Вследствие этого и в окончательном значении расчетной погрешности должны быть оставлены только первые одна – две значащие цифры. При этом необходимо учитывать следующее. Если полученное число начинается с цифры 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30 – 50%), это недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, то есть указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности. В итоге можно сформулировать правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения: 1. Абсолютная погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, – если первая есть 3 и более. 2. Среднее значение измеренной величины округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности. 3. Относительную погрешность, выраженную в процентах, достаточно записать двумя значащими цифрами. 4. Округления производится лишь в окончательном ответе, а все предварительные вычисления будут с одним-двумя лишними знаками. Пример: На вольтметре класса точности 2,5 с пределом измерений 300 В были произведены несколько повторных измерений одного и того же напряжения. При этом оказалось, что все замеры дали одинаковый результат 267,5 В. Отсутствие различий между знаками говорит о том, что случайная погрешность пренебрежимо мала, поэтому суммарная погрешность совпадает с систематической (см. рис. 1.3 а). Сначала найдем абсолютную, а затем относительную погрешности. Абсолютная погрешность градуировки прибора равна:
Так как первая значащая цифра абсолютной погрешности больше трех, то это значение должно быть округлено до 8 В. Относительная погрешность:
В значении относительной погрешности должны быть сохранены два значащих разряда 2,8% Таким образом, в окончательном ответе должно быть сообщено “Измеренное напряжение U =(268+8) В при относительной погрешности dU =2,8% ”. Краткая теория Все тела в природе притягивают друг друга. Закон, которому подчиняется это притяжение, был установлен Ньютоном и носит название закона Всемирного тяготения. Согласно этому закону сила, с которой две материальные точки притягивают друг друга, пропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними:
где g – Всемирная гравитационная постоянная, равная m 1, m 2 – массы взаимодействующих точек; r – расстояние между телами. Если тела не являются материальными точками, задача нахождения сил взаимодействия усложняется. Но если взаимодействующие тела представляют собой однородные шары или однородный шар и материальную точку, то их взаимодействие описывается формулой (2.1), где под r нужно понимать расстояние между центрами взаимодействующих тел. Притяжение тел осуществляется через гравитационное поле. Оно проявляет себя в том, что помещенное в него другое тело оказывается под действием силы притяжения. Гравитационное поле имеет две важных характеристики: силовую Напряженность
где Потенциалом гравитационного поля j называют:
где Uгр – потенциальная энергия, которой обладает в этом поле масса. Напряженность и потенциал связаны между собой соотношением:
Зная напряженность, можно вычислить разность потенциалов между точками 1 и 2 гравитационного поля:
Потенциальную энергию материальной точки массой m в гравитационном поле можно выразить так:
Если одно из взаимодействующих тел – Земля, то гравитационная сила называется силой тяжести. Движение под действием этой силы называется свободным падением, а ускорение, вызываемое этой силой, g – ускорением свободного падения. При точном решении задач о движении тел относительно земной поверхности нужно учитывать центробежную силу инерции, возникающую во вращающейся (по отношению к инерциальным системам) системе отсчета. Она равна (рис. 2.1):
где m – масса тела, w – угловая скорость суточного вращения Земли, RЗ – радиус Земли, j – широта местности.
 
Рис. 2.1 Наблюдаемое относительно Земли ускорение свободного падения тел Отличие силы тяжести Методика проведения измерений и описание установки Эксперимент состоит в определении ускорения свободного падения тел различной массы. Общий вид установки Атвуда показан на рисунке 2.2.
Электромагнит, после подведения к нему питающего напряжения, при помощи фрикционной муфты, удерживает систему ролика с грузиками в состоянии покоя. Верхний и средний кронштейны можно перемещать вдоль колонки и фиксировать в любом положении, устанавливая таким образом длину пути равномерноускоренного и равномерного движений грузика 14. Для облегчения определения этих путей на колонке имеется миллиметровая шкала, все кронштейны имеют указатель положения, а верхний кронштейн - дополнительную черту, облегчающую точное согласование нижней грани верхнего, большого грузика с определенным началом пути движения.
Нижний кронштейн оснащен фотоэлектрическим датчиком с оптической осью на уровне указателя положения кронштейна, после пересечения которой нижней гранью падающего грузика образуется электрический сигнал, указывающий прохождение грузиками определенного пути. На основании прибора, прикрепленного к нему жестко, находится миллисекундомер РМ-15. Через ролик, смонтированный на подшипнике таким образом, чтобы он мог вращаться с возможно малым сопротивлением, проходит нитка с двумя одинаковыми грузиками массой М каждый (14 и 8). Система при этом находится в равновесии. Если по одну сторону блока прибавим небольшой грузик массой m (13), тогда система получит ускорение под влиянием силы mg и, передвигаясь с ускорение а, пройдет путь S. По второму закону Ньютона для грузиков слева и справа (рис. 2.3):
Решая систему этих уравнений, получим:
Из законов кинематики
где t – время, в течение которого грузик 14 пройдет путь Н, двигаясь равномерно. Из формул (2.9) и (2.10) ускорение a равно:
Подставляя (2.11) в (2.8), получим расчетную формулу для нахождения ускорения свободного падения:
Формула (2.13) выведена в предположении, что сила трения и масса ролика нити пренебрежимо малы, нить нерастяжима. Порядок выполнения работы 1. При помощи регулируемых ножек основания привести колонку прибора к вертикальному положению. 2. Передвинуть средний кронштейн на избранную высоту, благодаря чему будет определен путь Н. 3. Передвинуть верхний кронштейн на заданную высоту, таким образом будет определен путь S. 4. Нажать клавишу «СЕТЬ», проверяя, все ли индикаторы измерителя высвечивают нуль. 5. На правый большой грузик М положить один из дополнительных грузиков массой m. 6. Согласовать нижнюю грань правого грузика с чертой, нанесенной на верхнем кронштейне. 7. Измерить при помощи шкалы на колонке заданные пути равноускоренного S и равномерного Н движений большого грузика. 8. Нажать клавишу «ПУСК». 9. Записать измеренное значение времени движении большого грузика на пути Н в таблицу 2.1. 10. Измерение повторить не менее 5 раз, устанавливая различные дополнительные грузики m и их комбинации для выбранных S и H. Полученные данные записать в таблицу 2.1, туда же занести рассчитанные значения (2 M + m) H 2 и 2 mSt 2. Таблица 2.1 – Результаты измерений S 1 = ____ м; H 1 = _____ м
11. Изменить параметры S и H, повторить измерения t как в пункте 10, данные занести в таблицу 2.2. Таблица 2.2 – Результаты измерений S 1 = ____ м; H 1 = _____ м
Краткая теория В данной работе изучаются свободные незатухающие гармонические колебания, подчиняющиеся следующему закону:
В этом уравнении: А – амплитуда колебаний, т.е. наибольшее отклонение маятника из положения равновесия,
Математическим маятником называют идеальную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Отклонение маятника от положения равновесия можно характеризовать углом j, образованным нитью с вертикалью (рис. 3.1). При отклонении маятника от положения равновесия возникает вращающий момент М, созданный силой
где m – масса, l – длина маятника. Уравнение динамики для вращательного движения имеет вид:
где I – момент инерции маятника, равный ml 2 (для материальной точки),
Приравняв выражения (3.3) и (3.4), получим
Приведем уравнение к виду
В случае малых колебаний
то получим дифференциальное уравнение второго порядка:
Оно имеет решение (сравните с 3.1)
Из формул (3.2) и (3.7) выразим период колебаний математического маятника
где l – длина математического маятника. Полученное соотношение (3.10) может быть использовано для определения ускорения свободного падения g. Для этого необходимо измерить Т, и l и выразить через них g с помощью формулы (3.10). Физический маятник Физическим маятником называют тело массой m произвольной формы и размеров, свободно колеблющееся вокруг оси, не проходящей через центр тяжести (рис. 3.2). При отклонении маятника на небольшой угол j он начнет колебаться около положения равновесия под действием составляющей
где m – масса,
Рис. 3.2 – Физический маятник Используя основной закон динамики вращательного движения (
где e – угловое ускорение (см. 3.3), I 0 – момент инерции маятника относительно оси качания О. При малых углах отклонения маятника от положения равновесия Приведем уравнение (3.9) к виду
и введя обозначение
имеем,
или
Частным решением дифференциального уравнения (3.13) является:
где
Период колебания
Достоинством метода оборотного физического маятника для определения ускорения свободного падения является то, что I 0 и l не входят в расчетную формулу для g. Перейдем к обсуждению этого метода. Согласно теореме Штейнера, момент инерции относительно оси качания О
где Iс – момент инерции маятника, относительно оси, параллельной оси качания и проходящей через центр масс С маятника. Подставляя (3.17) в (3.16), получаем
Попробуем найти такие два положения l 1 и l 2 (l 1¹ l 2) опорных призм по разные стороны от центра масс, чтобы периоды колебаний маятника совпадали: Т (l 1) = Т (l 2). Как видно из (3.18), для этого необходимо выполнение равенства
которое имеет место либо при l 1= l 2, либо при
В последнем случае период колебаний маятника
Следовательно, ускорение свободного падения может быть определено по формуле:
Как видно из (3.21), для нахождения g достаточно измерить только две величины: расстояние (l 1+ l 2) между опорными ребрами призм, период колебаний маятника в положении l 1 и в «перевернутом» положении l 2, при котором l 1¹ l 2. При этом периоды колебаний должны совпадать, т.е. должно выполняться равенство: Т (l 1)= Т (l 2)= Т. Из формул (3.8) и (3.16) видно, что математический маятник с длиной Величина lпр называется приведенной длиной физического маятника. Значит, приведенная длина физического маятника – это длина такого математического маятника, у которого период совпадает с периодом колебаний данного физического маятника. Порядок выполнения работы Определение ускорения свободного падения при помощи математического маятника 1. Нижний кронштейн вместе с фотоэлектрическим датчиком установить в нижней части колонки, обращая внимание на то, чтобы верхняя грань кронштейна показывала на шкале длину не менее 50 см. Затянуть вороток, фиксируя фотоэлектрический датчик в выбранном положении. 2. Поворачивая верхний кронштейн, поместить над датчиком математический маятник, установив предварительно его длину. 3. Включить миллисекундомер нажатием кнопки «СЕТЬ». 4. Вывести математический маятник из положения равновесия на 4-6°, отпустить его и нажать на кнопку «СБРОС». 5. После подсчета 10-20 колебаний нажать клавишу «СТОП». Записать время t и количество колебаний n. 6. По шкале прибора определить длину l маятника. 7. Повторить измерения для 5-7 различных длин маятника, для каждой фиксированной длины измерения провести по 3 раза. 8. Полученные данные занести в соответствующее количество (5-7) таблиц, аналогичных таблице 3..1 Таблица 3.1 – Длина маятника l = ________ (м)
Определение ускорения свободного падения при помощи оборотного маятника 1. Повернуть верхний кронштейн на 180°. 2. Зафиксировать подвижные грузы на стержне согласно рисунку 3.3. несимметрично, таким образом, чтобы один из них находился вблизи конца стержня, а другой – вблизи его середины. 3. Закрепить маятник на верхнем кронштейне на ноже, находящемся вблизи конца стержня. 4. Нижний кронштейн вместе с фотоэлектрическим датчиком переместить таким образом, чтобы стержень маятника пересекал оптическую ось. 5. Определить время t 10-20 полных колебаний оборотного маятника и определить период 6. Снять маятник и закрепить его на втором ноже. Проделать аналогичные измерения и определить период 7. Сравнить Т (l 2) с величиной Т (l 1). 8. Если 9. Повторно измерить периоды Т (l 1) и T (l 2) и сравнить их между собой. 10. Изменить положение второго ножа до момента получения равенства
Полученное зн
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 1677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.67.90 (0.018 с.) |

 = 1 мм при измерении стола L 1, это хорошее качество измерения, а если та же погрешность
= 1 мм при измерении стола L 1, это хорошее качество измерения, а если та же погрешность  = 1 мм имеет место при измерении диаметра карандаша L 2, это невысокое качество измерения.
= 1 мм имеет место при измерении диаметра карандаша L 2, это невысокое качество измерения. , или в процентах:
, или в процентах:  .
. ;
; .
. . (1.3)
. (1.3) =
=  .
. Видно, что абсолютная погрешность в этом случае лишь на 10% больше, чем случайная. То есть если бы систематической погрешности вообще не было, то в нашем примере это мало бы повлияло на общую абсолютную погрешность. Теперь учтем, что погрешность редко удается оценить с точностью лучше чем 10-20%, тогда в нашем случае можно положить D=D сл, то есть систематической погрешностью D с можно вообще пренебречь.
Видно, что абсолютная погрешность в этом случае лишь на 10% больше, чем случайная. То есть если бы систематической погрешности вообще не было, то в нашем примере это мало бы повлияло на общую абсолютную погрешность. Теперь учтем, что погрешность редко удается оценить с точностью лучше чем 10-20%, тогда в нашем случае можно положить D=D сл, то есть систематической погрешностью D с можно вообще пренебречь.




 , (2.1)
, (2.1) ,
, и энергетическую j.
и энергетическую j. , (2.2)
, (2.2) – гравитационная сила, действующая на материальную точку массы m.
– гравитационная сила, действующая на материальную точку массы m. , (2.3)
, (2.3) . (2.4)
. (2.4) . (2.5)
. (2.5) , а если гравитационное поле само создано материальной точкой или сферическим телом массой M, то потенциальную энергию материальной точки массой m можно найти следующим образом:
, а если гравитационное поле само создано материальной точкой или сферическим телом массой M, то потенциальную энергию материальной точки массой m можно найти следующим образом: .
. (2.6)
(2.6)


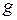
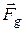 , с которой тело притягивается Землей, и силы
, с которой тело притягивается Землей, и силы  . Результирующая этих сил
. Результирующая этих сил  есть сила тяжести, равная
есть сила тяжести, равная  (
( – ускорение свободное падения, учитывающее вращение Земли).
– ускорение свободное падения, учитывающее вращение Земли). от силы притяжения к Земле
от силы притяжения к Земле  равна нулю на полюсах и достигает максимума, равного 0,3% силы
равна нулю на полюсах и достигает максимума, равного 0,3% силы  сама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0,2% меньше, чем у полюсов. В итоге ускорение свободного падения изменяется с широтой в пределах от 9,780 м/с 2 на экваторе до 9,832 м/с 2 на полюсах. Значение g =9,80665 м/с 2 принято в качестве нормального (стандартного) значения.
сама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0,2% меньше, чем у полюсов. В итоге ускорение свободного падения изменяется с широтой в пределах от 9,780 м/с 2 на экваторе до 9,832 м/с 2 на полюсах. Значение g =9,80665 м/с 2 принято в качестве нормального (стандартного) значения. На вертикальной колонне 1, установленной на основании 2, закреплены три кронштейна: неподвижный нижний кронштейн 3 и два подвижных: средний 4 и верхний 5, а также верхняя втулка 6. На верхней втулке закреплен ролик 7 и электромагнит 11. Через ролик проходит нить 12 с привязанными на ее концах грузиками 14 и 8.
На вертикальной колонне 1, установленной на основании 2, закреплены три кронштейна: неподвижный нижний кронштейн 3 и два подвижных: средний 4 и верхний 5, а также верхняя втулка 6. На верхней втулке закреплен ролик 7 и электромагнит 11. Через ролик проходит нить 12 с привязанными на ее концах грузиками 14 и 8. На среднем кронштейне закреплен кронштейн 9 и фотоэлектрический датчик 10. Кронштейн 9 снимает с падающего вниз большого грузика дополнительный грузик 13, а фотоэлектрический датчик в это время образует электрический импульс, сигнализирующий начало равномерного движения больших грузиков. Оптическая ось фотоэлектрического датчика (черта на его корпусе) находится на уровне указателя положения среднего кронштейна.
На среднем кронштейне закреплен кронштейн 9 и фотоэлектрический датчик 10. Кронштейн 9 снимает с падающего вниз большого грузика дополнительный грузик 13, а фотоэлектрический датчик в это время образует электрический импульс, сигнализирующий начало равномерного движения больших грузиков. Оптическая ось фотоэлектрического датчика (черта на его корпусе) находится на уровне указателя положения среднего кронштейна. , (2.7)
, (2.7) . (2.8)
. (2.8) (2.9)
(2.9) , (2.10)
, (2.10) , (2.11)
, (2.11) . (2.12)
. (2.12) . (2.13)
. (2.13)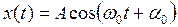 , (3.1)
, (3.1) – циклическая или круговая частота колебаний, t – время,
– циклическая или круговая частота колебаний, t – время,  – начальная фаза колебания,
– начальная фаза колебания,  – фаза колебания в момент времени t с. Периодом колебания маятника Т называют время, в течение которого маятник совершает одно полное колебание. Циклическая частота и период связаны соотношением:
– фаза колебания в момент времени t с. Периодом колебания маятника Т называют время, в течение которого маятник совершает одно полное колебание. Циклическая частота и период связаны соотношением: . (3.2)
. (3.2) Математический маятник
Математический маятник , являющейся составляющей силы тяжести
, являющейся составляющей силы тяжести  . Численное значение вращающего момента равно:
. Численное значение вращающего момента равно: , (3.3)
, (3.3) , (3.4)
, (3.4) – угловое ускорение, равное второй производной угла отклонения
– угловое ускорение, равное второй производной угла отклонения  по времени
по времени . (3.5)
. (3.5) .
. . (3.6)
. (3.6) и, если ввести обозначение
и, если ввести обозначение , (3.7)
, (3.7) . (3.8)
. (3.8) . (3.9)
. (3.9) , (3.10)
, (3.10) силы тяжести маятника
силы тяжести маятника 
 l – расстояние от точки подвеса до центра тяжести.
l – расстояние от точки подвеса до центра тяжести.
 ) имеем:
) имеем: ,
,
 , (3.11)
, (3.11) , (3.12)
, (3.12) . (3.13)
. (3.13) - циклическая частота колебаний, равная
- циклическая частота колебаний, равная . (3.15)
. (3.15) . (3.16)
. (3.16) Полученное соотношение (3.16) также может быть использовано для определения ускорения свободного падения g. Для этого необходимо измерить Т, I 0 и l и выразить через них g с помощью формулы (3.16). Оказывается, однако, что с высокой точностью можно измерить только период колебания Т маятника, а величины I 0 и l достаточно точно измерить не удается. Для этой цели удобно использовать оборотный маятник, т.е. маятник, представляющий собой массивный стержень (1), с двух концов которого закреплены параллельные друг другу опорные призмы (ножи) (2), за которые маятник может поочередно подвешиваться. Вдоль стержня могут перемещаться и закрепляться тяжелые грузы (3) (см. рис. 3.3).
Полученное соотношение (3.16) также может быть использовано для определения ускорения свободного падения g. Для этого необходимо измерить Т, I 0 и l и выразить через них g с помощью формулы (3.16). Оказывается, однако, что с высокой точностью можно измерить только период колебания Т маятника, а величины I 0 и l достаточно точно измерить не удается. Для этой цели удобно использовать оборотный маятник, т.е. маятник, представляющий собой массивный стержень (1), с двух концов которого закреплены параллельные друг другу опорные призмы (ножи) (2), за которые маятник может поочередно подвешиваться. Вдоль стержня могут перемещаться и закрепляться тяжелые грузы (3) (см. рис. 3.3). , (3.17)
, (3.17) (3.18)
(3.18) ,
,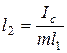 . (3.19)
. (3.19) . (3.20)
. (3.20)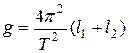 . (3.21)
. (3.21) будет иметь такой же период, что и физический маятник.
будет иметь такой же период, что и физический маятник. , (c 2)
, (c 2)
 .
. .
. , то второй нож переместить в направлении груза, находящегося в конце стержня, а если
, то второй нож переместить в направлении груза, находящегося в конце стержня, а если  - то в направлении середины стержня.
- то в направлении середины стержня. с точностью до 0,5%, т.е. до выполнения неравенства
с точностью до 0,5%, т.е. до выполнения неравенства или
или  .
.


