
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: будова атома. Теорія Бора
ПЛАН 1. Досліди Резерфорда з розсіяння a- частинок. Ядерна модель атома. 2. Атом водню та його спектр із теорії Бора. 3. Суцільний рентгенівський спектр і його короткохвильова межа. 4. Лінійчастий рентгенівський спектр. Закон Мозлі.
1. У другій половині минулого століття відкриття в різних галузях науки (періодичний закон Менделєєва, рентгенівські промені, радіоактивність) поставили під сумнів існуючі раніше уявлення про атом як неподільну частку.
+
a=180°
Основою сучасних уявлень про будову атома є досліди Резерфорда з розсіювання a-частин при проходженні через золоту фольгу. Із неспроможності пояснити ефект відхилення a-частин на основі існуючих уявлень, Резерфорд теоретично розв’язав задачу про розсіяння частинок у кулоновському полі, яке складалось із Р позитивних зарядів. Порівняльний аналіз результатів експериментів та розрахунків дозволив установити: 1) P = Z, де Z - порядковий номер елемента у таблиці Менделєєва. 2) В атомі містяться Z-електронів. Було запропоновано ядерну модель атома: у середині атома існує позитивний центр - ядро атома, навколо якого рухаються електрони, причому розміри ядра» 10-15 м, а діаметр атома ≈ 10-10 м. å me << mядра
10-15 м

Але ядерна модель не в змозі була пояснити два питання відповідно до законів класичної електродинаміки: 1) електрон повинен був випромінювати безперервну електромагнітну хвилю, але експеримент указує на те, що спектри випромінювання атомів дискретні. 2) випромінюючи електромагнітну хвилю, електрон повинен, втрачаючи енергію, згодом “впасти на ядро”, але атоми дуже стійкі.
Що ж відбувається насправді!?
2. Вивчаючи лінійчасті спектри атома водню, Бальмер у 1865 році встановив формулу для знаходження n або l у спектрі атома водню.
с = 3. 108 м/с - швидкість світла у вакуумі, R = 1,097 . 107 м-1 - стала Рідберга, n = 3, 4, 5... Усі лінії спектра, які відзначаються різним n, утворюють серію ліній. Узагальнуючи одержаний результат, Рідберг установив, що існують й інші серії ліній, а загальна формула для їх опису має вигляд:
n - номер орбіти (рівня), з якої “зникає” електрон,
к - номер рівня, на якому він з’являється.
к = 1,2; 3,4. n = к+1; к+2. к, n - номери орбіт електронів у вакуумі. (1) і (2) - формули для розрахунку частоти випромінювального світла.
Напишемо характерні існуючі серії: Якщо к = 1 n = 2,3... Лайман (УФ-область) к = 2 n = 3,4... Бальмер (видима область) к = 3 n = 4,5... Пашен (ІЧ-область) к = 4 n = 5,6... Брег(ІЧ-область) к = 5 n = 6,7... Пфунд(ІЧ-область) к = 6 n = 7,8... Хемфрі(ІЧ-область) Для воднеподібного іона (іон з одним електроном) формула (2) переходить:
Z - заряд ядра.
Однак ці експерименти знаходились у суперечності з класичними уявленнями про рух електрона в атомі, що і привело до створення некласичної (напівквантової) теорії Бора (1910 р.), яка певним чином на той час дозволила узгодити: 1) емпиричні закономірності лінійчастих спектрів, 2) ядерну модель атома, 3) квантовий характер випромінювання та поглинання світла атомами.
У теорії Бора поведінка електрона в атомі “регулюється” трьома постулатами: I. (Для стаціонарних станів): Існують такі стаціонарні стани для атомів, у яких атом не випромінює і не поглинає енергії. Це відповідає руху електрона по відповідній орбіті. II. Правило квантування орбіт: У стаціонарному стані електрон рухається по орбіті, рівняння якої має такий вигляд:
n = 1, 2, 3... vn - швидкість електрона масою m по орбіті радіуса rn із номером n. h - 6,626. 10-34 Дж.с -стала Планка.
III. Правило частот. При переході електрона в атом із однієї орбіти на іншу атом або поглинає, або випромінює квант енергії Е = hn, який дорівнює в точності різниці енергії рівнів атомів у цих стаціонарних станах.
Опишемо математично рух електрона в атомі:
m.aд.ц. = Fкул.; ад.ц. = vn2 / rn
Спільне рішення (6) і (4) дає
Для атома водню n = 1, Z = 1.
- перший боровський радіус (збігається з висновками ядерної моделі Резерфорда).
Повна енергія електрона в атомі:
Підстановка із (7) rn у цей вираз дає
Одержали дискретні (квантові) енергії електрона в атомі. n - квантове число, n = 1 - головний стан, n > 1 - збуджений стан.
При n®¥ и іонізація атома.
- потенціал іонізації
H: n = 1; Z = 1; ji = -13,59 eV. Тепер стало зрозумілоими спектральні особливості атома водню.
3. Рентгенівські промені були відкриті Рентгеном у 1895 р. і являють собою жорстке короткохвильове випромінювання, яке виникає внаслідок гальмування прискорених електронів.
~ кВ
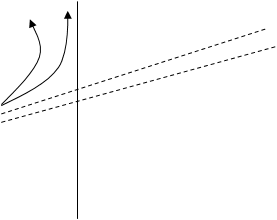
Експерименти показали, що при енергіях електронів, які не перевищують деяких критичних значень, визначених властивостями речовини анода, виникає суцільний рентгенівський спектр. Це випромінювання імітується самими електронами.
І
j2
j1
l min l
Це випромінювання буде обмежено з боку довжин хвиль або частот (lmin,nmax). j - потенціал, який подається на електрод рентгенівської трубки.
На основі збереженої енергії маємо: hnmax = Wк hnmax - енергія рентгенівського кванту, Wк - кінетична енергія електрона. Wк = еj
4. Поряд із гальмовим випромінюванням існує характеристичне рентгенівське випромінювання, яке характеризує речовину анода. Воно має не суцільний, а лінійчастий спектр.
+Ze
K L M N
При віддаленні електрона з К оболонки і вище на вільне місце приходить електрон, що супроводжується випромінюванням рентгенівського фотона, частота якого визначається законом Мозлі:
s - стала екранування, яка визначається фізико-хімічними властивостями речовини анода.
ЛЕКЦІЯ ХХII ТЕМА: ЕЛЕМЕНТИ КВАНТОВОЇ МЕХАНІКИ ПЛАН 1. Корпускулярно-хвильовий дуалізм. Гіпотеза Луї де Бройля. 2. Співвідношення невизначеності Гейзенберга. 3. Хвильова функція та її статистичний зміст. 4. Рівняння Шредінгера. 5. Рівняння Шредінгера для атома водню. Квантові числа. 6. Спін електрона. Дослід Штерна і Герлаха. 7. Принцип Паулі. 8. Розподіл електронів у атомі за станами.
1. Розглянена нами теорія Бора була значним кроком у розвитку теорії атомів. Вона показала: 1) неспроможність застосування законів класичної фізики до явищ у середині атомів; 2) визначне значення квантових законів у мікросвіті. Однак вона 1) не змогла побудувати теорію атома гелію, 2) їй була притаманна внутрішня суперечність.
У зв’язку з цим виникло питання про те, наскільки повним є уявлення про електрона як механічної частки з певними координатами та імпульсами. Якісним кроком на шляху до нових уявлень була гіпотеза Луї де Бройля про те, що корпускулярно-хвильовий дуалізм властивий не тільки електромагнітним хвилям, але й будь-яким елементарним частинкам. Таким чином, потоку елементарних частинок, які поширюються зі швидкістю v, відповідає певна електромагнітна хвиля з довжиною хвилі l (тобто поток частинок володіє властивостями плоскої хвилі).
l - довжина хвилі, h - стала Планка.
Якщо u ® c;
Експериментальне підтвердження цього - досліди Девідсона і Джермера із розсіяння електронів на монокристалі Нікеля, при цьому спостерігалось явище дифракції електронів (чисто хвильовий ефект).
Наявність max і min не можна було пояснити з законами класичної фізики. Однак найбільш дивне було в тому, що l електрона підрахована з цього досліду збігалася з такою, що була підрахована за формулою Вульфа-Брега, що дійсно пояснювала наявність у електроні хвильових властивостей.
2. Класична механіка стан будь-якої матеріальної точки визначає певними значеннями координат та часу. r = r (x, y, z, t) А як же бути з описом стану частинки у мікросвіті за умови наявності у ній хвильових властивостей згідно з гіпотезою де Бройля? Припустимо, що частинка знаходиться у деякій кінцевій області простору розмірами Dx, Dy, Dz. Можна припустити, що ця частинка у такому об’ємі буде приймати такі значення імпульсу Dpx, Dpy, Dpz, які задовольняють співвідношенням Гейзенберга. Dpx . Dx ³ h Dpy . Dy ³ h Dрz . Dz ³ h
Формула показує, що чим з більшою точністю Dx відома координата х, тим більша невизначеність у імпульсі Dpx ® ¥. Якщо частинка знаходиться у збудженому стані деякий час Dt, володіючи енергією Е, то її енергія також може бути задана тільки з точністю DЕ.
- співвідношення невизначеностей для енергій є одним із фундаментальних принципів квантової механіки (якщо електрон падає на ядро v Þ 0, то p = 0. Це суперечить основним положенням квантової механіки).
3. Із розглянутих вище двох питань видно, що описувати по-старому стан частинки не можна. А як же бути?! Для опису повединки мікрооб’єктів уводять поняття хвильової функції Y (x, y, z, t). Таким чином,
(3)
dW - імовірність того, що частинка знаходиться в елементі простору dV = dx dy dz. Але фізичний зміст має не сама функція, а квадрат її модуля |Y|2.
rw - густина імовірності, як раз вона і визначає ймовірність перебування частинки у даній точці простору. Слід сказати, що функція задовольняє такій вимозі нормування:
Фізичний зміст (5) у тому, що перебування частинки де-не-де у просторі є достовірною подією, ймовірність якої дорівнює 1.
4. Найважливіша проблема квантової механіки - знаходження рівняння аналогічного рівняння Ньютона у класичній механіці. Таке рівняння виведено Шредінгером у 1936 р. Це було рівняння для Y - функції:
m - маса частинки, яка має потенціальну енергію U(x, y, z) i - уявна одиниця, D - оператор Лапласа.
Для більшості фізичних явищ особливо важливим є знаходження незалежних від часу рішень рівняння Шредінгера, які називаються стаціонарними.
Для цього випадку
(7)
Підставивши (7) у (6),
- рівняння Шредінгера для стаціонарних станів.
Е - повна енергія частинки, яка рухається у потенціальному полі з енергією U. Математика дає розв’язок рівняння (8): це дає набір ji - власних функцій, які задовольняють рішення (8) та набір Еі - власних значень енергії. Таким чином, опис руху частинки зводиться до рішення рівняння Шредінгера, тобто до знаходження ji та Еі.
5. Застосуємо рівняння (8) до опису поведінки електрона в атомі водню. Можна показати на основі теорії діференційних рівнянь, що рівняння типу (8) мають рішення, які задовольняють вимоги однозначності, кінцевості та безперервності хвильової функції і її першої похідної тільки при таких значеннях власних енергії:
n = 1, 2, 3... Із формули (9) видно, що ми маємо дискретний спектр власних значень енергії, котрі отримали на основі рішення рівняння Шредінгера без якихось додаткових застосувань різних положень, як це було у теорії Бора. Ця формула в точності збігається з аналогічним результатом теорії Бора (8) по передньої лекції. Із (9) випливає фізично, що всі значення En < 0, а з цього виходить, що стан електрона є “зв’язаним”, тобто математично його стан можна описати як його знаходження у гіперболічній потенціальній ямі.
r
     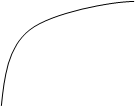  
Найнижчий рівень (n=1) відповідає основному станові системи, а всі рівні En>E1 (n=2,3...) - збуджені стани. Зі збільшенням n рівні будуть ще тісніше, а при n®¥, Е®0. Слід відмітити, що випадок з En>0 теж може випливати із розв’язання рівняння Шредінгера. Фізично це означає рух електрона поблизу ядра або на ¥, а це і є іонізація. n = 1; z = 1;
У квантовій механіці доводиться, що рівняння Шредінгера задовольняють тільки такі власні функції, що визначаються певними квантовими числами. Введемо числа: 1) n - головне квантове число, згідно з (9) воно приймає значення: 1) (10)
Фізичний зміст n полягає у тому, що воно визначає номер енергетичного рівня електрона в атомі і приймає тільки дискретні значення. 2) Із рішення рівняння Шредінгера випливає, що момент імпульсу електрона (механічний орбітальний момент) теж квантується за формулою
l = 0, 1, 2, 3... (n-1) (12) Фізичний зміст l полягає в тому, що воно визначає момент імпульсу електрона в атомі і кожному значенню n відповідає орбітальне квантове число. Згідно з теорією Бора припускається, що при прикладенні до атома зовнішнього магнітного поля вектори механічного моменту L і магнітного моменту `Pn будуть орієнтовані довільним чином відносно напрямку зовнішнього магнітного поля. Ця помилка усувається у квантовій механіці введенням просторового квантування. Із розв’язання рівняння Шредінгера виходить:`Le може приймати не всі орієнтації у просторі, а тільки такі, при яких квантується його проекція на напрямок зовнішнього магнітного поля:
(13)
де Lez – проекція механічного моменту на напрямок зовнішнього магнітного поля. 3) m – магнітне квантове число
(14)
Видно із (11), (13), (14), що Le може приймати (2l + 1) значень.
6. Для підтвердження ідеї просторового квантування Штерном і Герлахом у 1926 р. були проведені досліди з вимірювання магнітних моментів атомів різних хімічних елементів за величиною сили, діючої на атом у неоднорідному магнітному полі.
S N
- Ag Атоми срібла, за даними дослідами, відхилялися двояким чином у магнітному полі, що вказувало і відповідало двом орієнтаціям магнітного моменту атома. Але стан електронів у атомах розглядуваних хімічних елементів відповідали значенням l = 0 та m=0? Квантування якого моменту було знайдено? Для того, щоб результати досліду відповідали основним положенням квантової механіки, треба було ввести крім орбітального моменту електрона ` Le, власний механічний момент електрона `Les (спін) та власний магнітний момент електрона `Pes. Спін електрона ніяким чином не пов’язаний із рухом електрона у просторі. Спін – фундаментальна властивість будь-якої частинки. Згідно з основними положеннями квантової механіки визначається:
S– спінове квантове число. Аналогічно раніше введеному може бути 2s+1=2; S=1/2. Для спіну також характерне вторинне квантування
(16)
ms– магнітне спінове квантове число. 4) ms=±1/2
7. Таким чином, для характеристики електронного стану електрона в атомі треба задати тільки значення квантових чисел: n, l, m, ms `r =`r (x, y, z, t) Þ z= z(n, l, m, ms ) Зв’язок між цими числами регулюється принципом Паулі (1927 р.): У будь-якому атомі не може бути двох однакових електронів, які б знаходились у однакових стаціонарних станах і які б визначалися набором однакових чисел n, l, m, ms.
Принцип Паулі пов’язаний з основними обмеженнями квантової механіки та принципом нерозпізнаності частинок, із якого випливає існування двох класів частинок ферміонів і бозонів, для яких характерне існування анти- й симетричних функцій. S напівцілий y (-...) = -y () – ферміони (е, р, +n) S цілий y (-...) = +y () – бозони (фотони, гравітони, ядра хімічних елементів). Принцип Паулі з точки зору квантової механіки: ферміони зустрічаються в природі тільки у станах, які описуються антисиметричною функцією.
8. Користуючись принципом Паулі, можна знайти кількість електронів, які знаходяться у станах, що визначаються головним квантовим числом n.
l = 0; S - стан n=1 K – оболонка, 2 eл.
l = 1; p – стан l = 0; m=0; ms = ± 1/2, 2 eл. L = 2; d - cтан n = 2 l = 0,1 m = 0, ± 1 ms = ± 1/2 2 ел. 2S2 l = 0 l = 1 m =
ЛЕКЦІЯ ХХIII
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.11.34 (0.16 с.) |
 S
S



 *
*





 + -
+ -
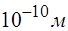
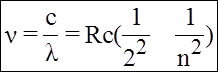 (1)
(1) Є (2)
Є (2) (3)
(3) (4)
(4)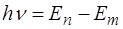

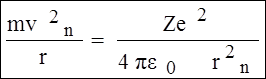 (6)
(6) (7)
(7)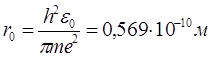
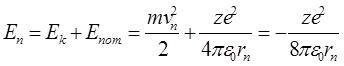 (з урахуванням (6))
(з урахуванням (6)) (8)
(8)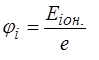
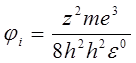
 вакуум
вакуум р. промені
р. промені


 А К
А К
 e
e -
-


 j3 j3 > j2 > j1
j3 j3 > j2 > j1


 (9)
(9)

 (np фотон)
(np фотон)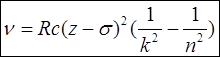 (10)
(10)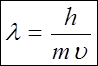 (1) 1924 р.
(1) 1924 р. (1а)
(1а) І
І 




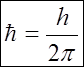 (2)
(2)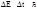
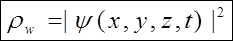 (4)
(4) (5) - умова нормування функції.
(5) - умова нормування функції. (6)
(6)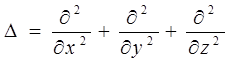
 (8)
(8) (9)
(9)
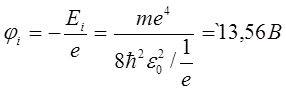

 (11)
(11)
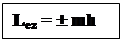
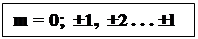


 + A
+ A
 10-5 мм рт. ст.
10-5 мм рт. ст.



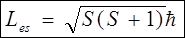 (15)
(15)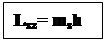

 6 ел. 2+6 = 8 ел.
6 ел. 2+6 = 8 ел.


