
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции, заданной неявно и параметрически.Содержание книги
Поиск на нашем сайте
Функция, заданная неявно Неявной функцией переменной Пусть дифференцируемая функция
Функция, заданная параметрически Пусть заданы две функции переменной
Задание этих функций означает задание функциональной зависимости между переменными Если в некотором интервале (a,b) функции
Тогда
Пример 4.7. Найти первую производную функции Решение Данная функция задано неявно. Продифференцируем тождество Выразим из получившегося тождества
Найдем значение первой производной в в точке
Пример 4.8. Найти первую и вторую производные функции Решение: Данная функция задано неявно. Продифференцируем тождество
Выразим из получившегося тождества
Из условия имеем
Найдем вторую производную, продифференцировав получившееся равенство по переменной x, имея в виду, что
Итак, имеем
Пример 4.9. Написать уравнение касательной и уравнение нормали к линии Решение
Нам необходимо написать уравнение касательной в точке Найдем производную, продифференцировав тождество
Разделим получившееся тождество на ln 2 и подставим вместо
Напишем уравнение касательной:
Напишем уравнение нормали:
Итак.
Пример 4.10. Найти первую и вторую производные функции, заданной параметрически: 1) Решение 1) Первую производную функции, заданной параметрически, найдем по формуле: Найдем производные функций Тогда
Вторую производную функции, заданной параметрически, найдем по формуле: Продифференцируем функцию
Тогда Таким образом:
2) Первую производную функции, заданной параметрически, найдем по формуле: Найдем производные функций
Тогда
Вторую производную функции, заданной параметрически, найдем по формуле: Продифференцируем функцию
Тогда Таким образом:
Пример 4.11. Написать уравнение касательной и уравнение нормали к кривой Решение
Найдем значение функции
Следовательно, Найдем значение функции
Следовательно, Вычислим производную функции по формуле Для этого найдем производные функций
Тогда по формуле
Следовательно, Напишем уравнение касательной:
Напишем уравнение нормали:
Итак.,
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.52.238 (0.009 с.) |

 называется функция, значения которой находятся из уравнения, связывающего
называется функция, значения которой находятся из уравнения, связывающего  , и не разрешенного относительно
, и не разрешенного относительно 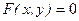 . Тогда производную
. Тогда производную  можно найти, дифференцируя тождество
можно найти, дифференцируя тождество  Производная функции, заданной неявно выражается через переменную
Производная функции, заданной неявно выражается через переменную 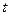 :
: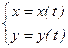 .
.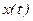 и
и 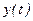 дифференцируемы и
дифференцируемы и 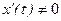 , то на интервале (a,b) функция
, то на интервале (a,b) функция 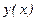 однозначно определена, дифференцируема и
однозначно определена, дифференцируема и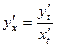 .
.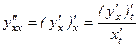
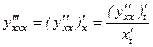 и т.д.
и т.д.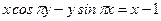 в точке
в точке 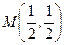 .
.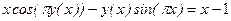 по переменной x, имея в виду, что
по переменной x, имея в виду, что 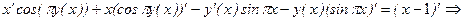
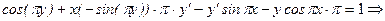
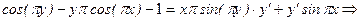
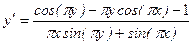 .
.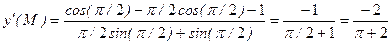
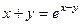 .
.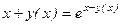 по переменной x, имея в виду, что
по переменной x, имея в виду, что 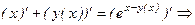
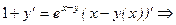
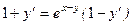 .
.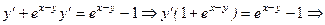
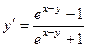 .
.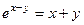 ; тогда
; тогда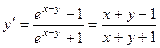 .
.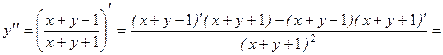
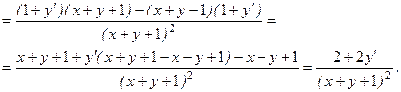
 Выражение для
Выражение для 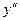 и получим:
и получим: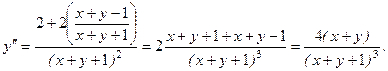
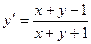 ;
;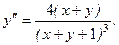
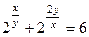 в точке
в точке 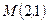 .
.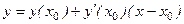 -уравнение касательной в точке
-уравнение касательной в точке  ;
;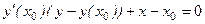 - уравнение нормали в точке
- уравнение нормали в точке  ; а
; а  .
.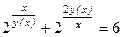 по переменной x, имея в виду, что
по переменной x, имея в виду, что 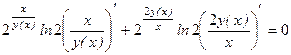 ;
;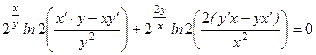 ;
;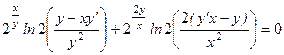 .
.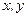 координаты точки М(
координаты точки М(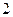 ;
; 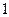 ), а затем найдем производную функции в точке М:
), а затем найдем производную функции в точке М: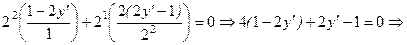
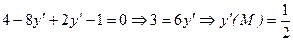 .
.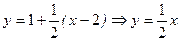 .
.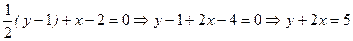 .
.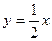 - уравнение касательной в точке М(2.1);
- уравнение касательной в точке М(2.1);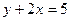 - уравнение нормали в точке М(2.1).
- уравнение нормали в точке М(2.1).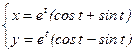 ; 2)
; 2) 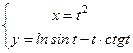 .
.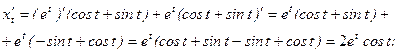
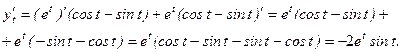
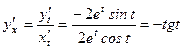 .
.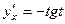 по переменной
по переменной 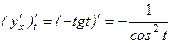 .
.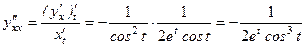 .
.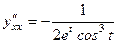 .
.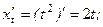
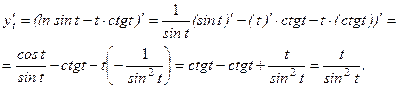
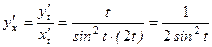 .
.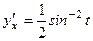 по переменной
по переменной 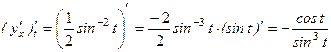 .
.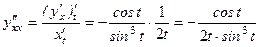 .
.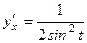 ;
;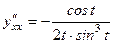
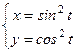 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра 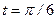 .
.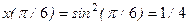 .
.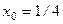
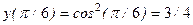 .
.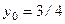
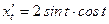 ;
;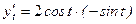
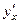 :
: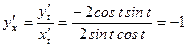 .
.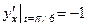 .
.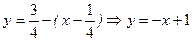 .
.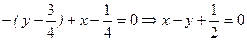 .
.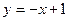 - уравнение касательной в точке М(2.1);
- уравнение касательной в точке М(2.1);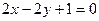 - уравнение нормали в точке М(2.1).
- уравнение нормали в точке М(2.1).


