
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о дифференцируемых функциях. Правило Лопиталя. Формула Тейлора.
Теорема Ролля Если функция 1) непрерывна на отрезке [ a, b ], 2) дифференцируема на интервале (a, b), 3) на концах отрезка принимает равные значения, т.е. тогда на интервале (a, b) существует по крайней мере одна точка
Все условия теоремы Ролля существенны, при нарушении хотя бы одного из этих условий утверждение теоремы может оказаться неверным. Например, непрерывная функция [ a, b ]. Например, функция Геометрический смысл теоремы Ролля заключается в следующем: если функция
Теорема Лагранжа
Если функция 1) непрерывна на отрезке [ a, b ], 2) дифференцируема на интервале (a, b), тогда на интервале (a, b) существует по крайней мере одна точка
Теорема Роля является частным случаем теоремы Лагранжа.
Следствия из теоремы Лагранжа 1.Если функция 2. Если функция дифференцируема на интервале (a, b) и для всех функция
Формула Коши Если функции 1) непрерывны на отрезке [ a, b ], 2) дифференцируемы на интервале (a, b), причем тогда на интервале (a, b) существует по крайней мере одна точка
Правило Лопиталя.
Пусть функции f (x) и g (x) дифференцируемы в некоторой проколотой окрестности точки а, причем
Тогда
Пример 4.11. Вычислить пределы, используя правило Лопиталя: 1) 3) 5) 7) 9) Решение 1) 2) 3) 4) 5)
Второй предел в данном произведении при в первом же пределе получили снова неопределенность вида 6) 7)
8)
9) Вычислим предел: В данном пределе имеем неопределенность вида Вычислим предел по правилу Лопиталя:
Следовательно, 10)
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.31.73 (0.016 с.) |

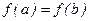 ,
, , в которой производная данной функции равна нулю, т. е.
, в которой производная данной функции равна нулю, т. е. .
. на концах отрезка [ -1, 1] имеет равные значения (
на концах отрезка [ -1, 1] имеет равные значения ( ), а вместе с тем ее производная нигде в ноль не обращается. В данном случае не выполнено второе условие теоремы Ролля: в точке
), а вместе с тем ее производная нигде в ноль не обращается. В данном случае не выполнено второе условие теоремы Ролля: в точке  , лежащей внутри интервала (-1,1), производная функции
, лежащей внутри интервала (-1,1), производная функции  имеет равные значения на концах отрезка [-1, 1]:
имеет равные значения на концах отрезка [-1, 1]:  , дифференцируема на интервале (-1,1), но ее производная во всех точках этого интервала равна 1, и, следовательно, нет точки, в которой производная равна нулю. Здесь нарушено первое условие теоремы, так как функция не является непрерывной на отрезке [ -1, 1]
, дифференцируема на интервале (-1,1), но ее производная во всех точках этого интервала равна 1, и, следовательно, нет точки, в которой производная равна нулю. Здесь нарушено первое условие теоремы, так как функция не является непрерывной на отрезке [ -1, 1]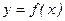 на некотором интервале удовлетворяет условиям теоремы Ролля, то на этом интервале найдется точка, в которой касательная параллельна оси абсцисс.
на некотором интервале удовлетворяет условиям теоремы Ролля, то на этом интервале найдется точка, в которой касательная параллельна оси абсцисс. ,
,  .
. для всех
для всех  , то
, то  на данном интервале.
на данном интервале. , то
, то  , т.е.
, т.е.
 во всех точках этого интервала,
во всех точках этого интервала, ,
,  и
и 
 также существует, причем
также существует, причем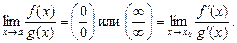
 ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  .
.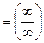
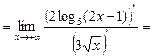

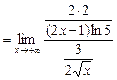



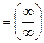



 = 0.
= 0.




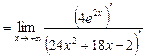



 = +¥.
= +¥.
 =
=


 =
=

 =
=


 = 0.
= 0.




 равен 1,
равен 1,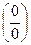 , еще раз применим правило Лопиталя:
, еще раз применим правило Лопиталя: 









 =
= 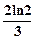 .
.






 .
.





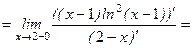


 .
.
 ;
; .
. .
.
 =
= =| по правилу Лопиталя|=
=| по правилу Лопиталя|=


 .
.



 .
.


