
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел последовательности, предел и непрерывность функции одной переменной.Стр 1 из 8Следующая ⇒
Предел последовательности, предел и непрерывность функции одной переменной. 3.1. Функции и основные понятия, связанные с ними. Пусть X – некоторое числовое множество. На множестве X определена числовая функция f, если каждому элементу x множества X ( Обычно функцию задают формулой, указывающей последовательность математических операций, которые необходимо выполнить над аргументом, чтобы получить ее значение. В этом случае под областью определения функции понимают множество тех значений аргумента, для которых указанные формулой действия выполнимы. Такой способ задания функции называется аналитическим. Табличный способ задания функции состоит в том, что указываются значения аргумента Функция f(x) задана графически, если на координатной плоскости изображен ее график. Графиком функции f(x) называется множество точек координатной плоскости с координатами (x, f(x)), т. е. множество точек, абсциссы которых принадлежат множеству X, а ординаты равны соответствующим значения функции. Функция f(x) определенная на множестве X, называется четной, если для любого - График четной функции симметричен относительно оси ординат. Функция f(x) определенная на множестве X, называется нечетной, если для любого - График нечетной функции симметричен относительно начала координат. Функция f(x) определенная на множестве X, называется периодической, если существует такое число Т >0, что для любого
Число Т называется периодом функции f(x). Функция f(x), называется ограниченной в окрестности точки
Сведения из элементарной математики Действия с многочленами
Разложение многочленов на множители Многочлен вида anxn + an –1 xn –1 … + a 0 можно разложить на множители по формуле: anxn + an– 1 xn– 1 +… + a 0 = an (x – x 1) (x – x 2)…(x – xn), где x 1, x 2, … xn – корни этого многочлена. Деление многочленов 1. Дробь вида
2. Деление многочлена на многочлен можно выполнить с остатком, подобно тому, как это делается при делении целых чисел. При делении многочлена на многочлен делят старший член многочлена-делимого на старший член многочлена-делителя, а затем частное от этого деления умножают на многочлен-делитель, и это произведение вычитают из многочлена-делимого. Затем повторяют то же самое до тех пор, пока деление не закончится или степень остатка не станет меньше степени многочлена-делителя. Пример 3.2. Разделить многочлен 2 x 3 – 3 x + 1 + 3 x 2 на многочлен x + 2. Решение 1) Записываем оба многочлена по убыванию степеней: 2 x 3 + 3 x 2 – 3 x + 1 | x + 2 2) Делим первый член делимого 2 x 3 на первый член делителя х. Результат 2 х 2 – есть первый член частного: 2 х 3 + 3 х 2 – 3 х + 1 | х + 2 2 х 2 3) Умножаем полученный член 2 х 2 на делитель х + 2, результат записываем под делимым: 2 х 3 + 3 х 2 – 3 х + 1| х + 2 2 х 3 + 4 х 2 2 х 2 4) Вычитаем члены результата из соответствующих членов делимого, сносим следующий по порядку член делимого: 2 х 3 + 3 х 2 – 3 х + 1 | х + 2 2 х 3 + 4 х 2 2 х 2 – х 2– 3 х 5) Делим получившийся первый член (– х 2) на первый член делителя х. Результат (– х) есть второй член частного: 2 х 3 + 3 х 2 – 3 х + 1 | х + 2 2 х 3 + 4 х 2 2 х 2 – х – х 2 – 3 х 6) Умножаем полученный член (– х) на делитель х +2, результат записываем под делимым. Вычитаем члены результата из соответствующих членов делимого, сносим следующий по порядку член делимого: 2 х 3 + 3 х 2 – 3 х + 1 | х + 2 2 х 3 + 4 х 2 2 х 2– х – х 2 – 3 х – х 2 – 2 х – х +1 7) Делим получившийся первый член (– х) на первый член делителя х. Результат (–1) есть третий член частного. Затем проделаем те же действия, что и в первых двух случаях: 2 х 3 + 3 х 2 – 3 х + 1 | х + 2 2 х 3 + 4 х 2 2 х 2 – х – 1 – х 2 – 3 х – х 2 – 2 х – х + 1 – х – 2 Получили остаток 3. Степень его меньше степени делителя. Деление закончено. Следовательно,
Пример 3.3. Разделить многочлен 2 х 4 + х 3 – 10 х 2 – 7 х + 2 на многочлен х 2 + 3 х + 2. Решение 2 х 4 + х 3 – 10 х 2 – 7 х + 2 | х 2 + 3 х + 2 2 х 4 + 6 х 3 + 4 х 2 2 х 2 – 5 х + 1 –5 х 3 – 14 х 2 – 7 х –5 х 3 – 15 х 2 – 10 х х 2 + 3 х + 2 – х 2 + 3 х + 2 т.е. Пример 3.4. Разделить многочлен – х 4 + х 3 + 2 х 2 + 3 х – 1 на многочлен x 2 + 3 x – 1. Решение Разделим многочлен – – х 4 + х 3 + 2 х 2 + 3 х – 1 | x 2 + 3 x – 1 – x 4 – 3 x 3 + 3 x – x 2 + 4 x – 11 4 x 3 + x 2 + 3 x 4 x 3 + 12 x 2 – 4 x –11 x 2 + 7 x – 1 –11 x 2 – 33 x + 11 40 x – 12 – Тогда Пример 3.5. Разложить на множители многочлены: б) (– х + 1)3 + (2 х + 3)3. Решение а) (– х + 1)2 – (2 х + 3)2 = (– х + 1 – 2 х – 3) (– х + 1 + 2 х + 3) = б) (– х + 1)3 + (2 х + 3)3 = (– х + 1 + 2 х + 3)((– х + 1)2 – (– х + 1) ´ Предел последовательности Последовательностью действительных чисел называется числовая функция Последовательность Последовательность Последовательность существуют такие числа m и M, что Число А называется пределом последовательности
Обозначение: С помощью логических символов определение предела последовательности записывается следующим образом:
Последовательность
Или с помощью логических символов:
Последовательность Последовательность Последовательность Последовательность Последовательность
Основные теоремы о сходящихся последовательностях. 1)Последовательность не может иметь двух различных пределов. 2)Сходящаяся последовательность ограничена. 3)Если последовательности
Если, кроме того,
4)Если для последовательностей 4) Если последовательность монотонна и ограничена, то она имеет предел (теорема Вейерштрасса).
Пример 3.8. Вычислить пределы последовательностей: 1) 7) Решение 1) 2) 3) 4) 5) 6)
8)
Предел функции Любой интервал, содержащий точку Функция f(x), называется ограниченной в окрестности
Определение предела функции. 1. По Коши. Пусть функция y = f (x) определена в некоторой проколотой окрестности Число a называется пределом функции f (x) в точке х 0 и обозначается
если для любого положительного числа Или с помощью логических символов:
Также определение предела функции можно записать, используя понятие окрестности:
2. По Гейне. Пусть функция y = f (x) определена в некоторой проколотой окрестности
Бесконечно большие функции. Пусть функция y = f (x) определена в некоторой проколотой окрестности Или с помощью логических символов:
Если
Односторонние пределы.
Пусть функция y = f (x) определена в некоторой проколотой окрестности Число а называется пределом функции при х ® x 0 + 0 справа ( Число а называется пределом функции при х ® x 0 – 0 слева ( Предел в бесконечности. Пусть функция y = f (x) определена для всех x, таких что Число а называется пределом функции при х ® ¥ (
. Основные теоремы о пределе функции. 1) Пусть при
Если, кроме того,
2)Если при 3) Если
3)Если
4) Если функция f(x), определенная в окрестности точки Замечательные пределы Частое применение находят следующие пределы:
или
Арифметика бесконечностей Пусть с = const, с ¹ 0, тогда: 1) с × ¥ = ¥; 5) –¥ – ¥ = –¥; 2) 3) 4) +¥ + ¥ = +¥; 8) Неопределенности Если при вычислении пределов получается выражение вида
называемое неопределенностью, то необходимо с помощью преобразований избавиться от этих неопределенностей. Бесконечно малые функции. Пусть функция y = f (x) определена в некоторой проколотой окрестности
Свойства бесконечно малых функций. 1)Сумма (разность) двух бесконечно малых функций при 2)Произведение бесконечно малой функции при x ® x 0 на ограниченную в некоторой проколотой окрестности точки x 0 функцию есть бесконечно малая функция при x ® x 0. Из определения предела функции следует, что число а является пределом функции f(x) в точке Сравнение бесконечно малых функций Пусть функции Бесконечно малые при x ® x 0 функции
Бесконечно малые при x ® x 0 функции Бесконечно малые при x ® x 0 функции
Бесконечно малая при x ® x 0 функция
Обозначение: Бесконечно малая при x ® x 0 функция
Таблица эквивалентных бесконечно малых Пусть a(x) ® 0, тогда sin a(x) ~ a(x) tg a(x) ~ a(x) 1 – cos a (x) ~ arcsin a (x) ~ a (x) arctg a (x) ~ a (x) a a(x) – 1 ~ a (x) ln a e a(x) – 1 ~ a (x) log a (1 + a (x)) ~ a (x) log a e ln (1 + a (x)) ~ a (x) (1 + a (x)) m – 1 ~ m ×a (x) Если a(x), b(х) – бесконечно малые фуекции и a(x) ~ a1(x),
При вычислении предела частного двух бесконечно малых одну из них или обе можно заменить эквивалентными им бесконечно малыми. Самые распространенные ошибки при вычислении предела некоторого выражения заключаются в замене функции Например, нельзя заменить бесконечно малую при Пример 3.9. Вычислить пределы функций: 1) 4) 6) 8) 10) 12) 14) 17) 20) 23) 26) 28) 30) 33) 35) 37)
Решение 1) 2) 3) = 4) 5) 6) 7) 8)
9) 10)
11) 12) Разложим числитель и знаменатель на множители:
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.158.92 (0.201 с.) |
 ) поставлено в соответствие действительное число f(x). Множество X называется областью определения функции. Произвольный элемент области определения обозначается буквой x и называется аргументом функции. Множество всех значений функции f(x), когда аргументпробегает область определения функции, называется множеством значений функции f.
) поставлено в соответствие действительное число f(x). Множество X называется областью определения функции. Произвольный элемент области определения обозначается буквой x и называется аргументом функции. Множество всех значений функции f(x), когда аргументпробегает область определения функции, называется множеством значений функции f. и соответствующие им значения функции
и соответствующие им значения функции  . При табличном задании функции, ее область определения состоит только из значений
. При табличном задании функции, ее область определения состоит только из значений  .
. .
. и
и  .
. , если существует такое число М> 0, что
, если существует такое число М> 0, что , для любого
, для любого  данной окрестности точки
данной окрестности точки  можно разложить на сумму дробей по формуле:
можно разложить на сумму дробей по формуле:
 .
. .
.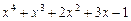 на многочлен
на многочлен  столбцом:
столбцом: целая часть; 40 x – 12 – остаток.
целая часть; 40 x – 12 – остаток. .
. , определенная на множестве всех натуральных чисел. Аргумент этой функции обозначается n, а сама функция -
, определенная на множестве всех натуральных чисел. Аргумент этой функции обозначается n, а сама функция -  . Таким образом, числовая последовательность задана, если указан закон, по которому каждому натуральному числу n ставится в соответствие определенное число
. Таким образом, числовая последовательность задана, если указан закон, по которому каждому натуральному числу n ставится в соответствие определенное число  называются членами последовательности. Принято обозначать последовательность символом:
называются членами последовательности. Принято обозначать последовательность символом: 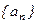 .
.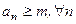 .
.
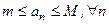 .
. существует такое натуральное число N, что при всех n>N выполняется неравенство:
существует такое натуральное число N, что при всех n>N выполняется неравенство: .
.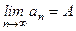

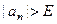 .
.

 .
. .
. .
. . Последовательность
. Последовательность  сходятся, то сходятся и последовательности
сходятся, то сходятся и последовательности  ;
;  , причем
, причем

 ;
;
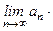
 и
и  , то последовательность
, то последовательность  также сходится и
также сходится и
 .
. , начиная с некоторого номера, выполняется неравенство
, начиная с некоторого номера, выполняется неравенство  и
и 
 ; 2)
; 2) 
 ;
;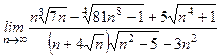 ;
;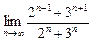 ; 6)
; 6)  ;
;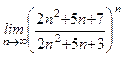 ; 8)
; 8) 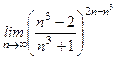 .
.
 =
=  =
=  =
=  =
=  =
= 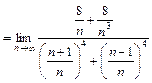 =
=  =
=  .
. =
=  =
= 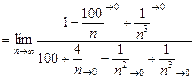 =
=  .
. = =
= =  =
=  .
.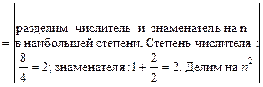 =
=  =
=  =
=  =
=  =
=  .
.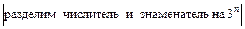 =
=  =
=  .
.
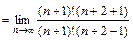 =
=
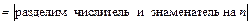 =
=  = 1. 7)
= 1. 7)  =
=


 =
=  называется
называется  - окрестностью точки.
- окрестностью точки. 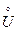
 (x 0)=
(x 0)= 
 называется проколотой
называется проколотой 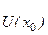 точки
точки  точки x 0, где r > 0 – некоторое число, тогда:
точки x 0, где r > 0 – некоторое число, тогда: ,
,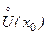 и удовлетворяющих неравенству 0 < | x – x 0| < d(e), будет верно неравенство | f (x) – a | < e.
и удовлетворяющих неравенству 0 < | x – x 0| < d(e), будет верно неравенство | f (x) – a | < e.


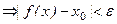 .
.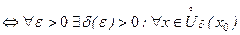
 значений аргумента х Î
значений аргумента х Î  сходится к числу а.
сходится к числу а.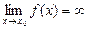 ), если для любого сколь угодно большого числа Е > 0 существует такое число d(Е) > 0 и зависящее от Е, такое, что для " х Î
), если для любого сколь угодно большого числа Е > 0 существует такое число d(Е) > 0 и зависящее от Е, такое, что для " х Î 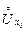 , из условия 0 < | x – x 0| < d(Е) следует условие | f (x)| > E.
, из условия 0 < | x – x 0| < d(Е) следует условие | f (x)| > E.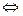

 .
. ), если для "e > 0 $ d(e) > 0, такое что для " х Î
), если для "e > 0 $ d(e) > 0, такое что для " х Î 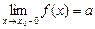 ),если для " e > 0 $ d(e) > 0, такого что для " х Î
),если для " e > 0 $ d(e) > 0, такого что для " х Î  .
.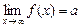 ), если для " e > 0 $ d(e) > 0, такое что для " х из условия | x | > d(e) следует неравенство | f (x) – a | < e.
), если для " e > 0 $ d(e) > 0, такое что для " х из условия | x | > d(e) следует неравенство | f (x) – a | < e.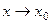 существуют конечные пределы функций
существуют конечные пределы функций  и
и  . Тогда при
. Тогда при 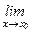 (f 1(x)
(f 1(x)  f 2(x)) =
f 2(x)) =  , то существует предел частного этих функций и
, то существует предел частного этих функций и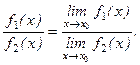
 для всех х Î
для всех х Î  и
и  имеют в точке
имеют в точке 
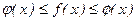 для всех х Î
для всех х Î  и
и  в точке
в точке  =
= 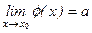 .
.
 – первый замечательный предел;
– первый замечательный предел;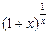 = e – второй замечательный предел,
= e – второй замечательный предел,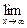
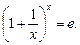
 6) (+¥) с = +¥;
6) (+¥) с = +¥; ; 7) (+¥)+¥ = +¥;
; 7) (+¥)+¥ = +¥; .
. ,
, .
. , где a(x) бесконечно малая функция при x ® x 0.
, где a(x) бесконечно малая функция при x ® x 0.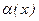 и
и  - бесконечно малые функции при x ® x 0.
- бесконечно малые функции при x ® x 0. 1.
1.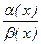 или
или  .
. .
.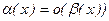 .
.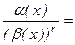 c
c 


 на эквивалентную бесконечно малую в случае, если функция
на эквивалентную бесконечно малую в случае, если функция 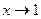 функцию
функцию  на функцию
на функцию  , так как при
, так как при  заменить функции
заменить функции  и
и  на эквивалентную им бесконечно малую при
на эквивалентную им бесконечно малую при  функцию
функцию  .
.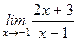 ; 2)
; 2)  ; 3)
; 3)  ;
;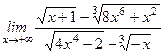 ; 5)
; 5)  ;
; ; 7)
; 7)  ;
; ; 9)
; 9)  ;
; ; 11)
; 11) 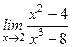 ;
;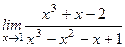 ; 13)
; 13)  ;
; ; 15)
; 15)  ; 16)
; 16)  ;
; ; 18)
; 18) 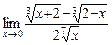 ; 19)
; 19)  ;
; ; 21)
; 21)  ; 22)
; 22)  ;
; ; 24)
; 24)  ; 25)
; 25)  ;
; ;27)
;27)  ;
; ; 29)
; 29)  ;
; ; 31)
; 31)  ; 32)
; 32)  ;
;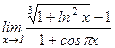 ; 34)
; 34)  ;
;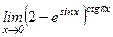 ; 36)
; 36) 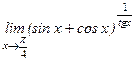 ;
;
 .
.
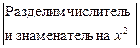 =
= 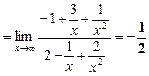 .
.
 .
. =
= 
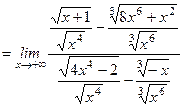 =
= 
 .
.
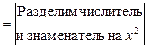 =
= 
 =
= 
 .
.
 =
=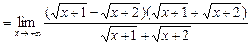
 =
= 
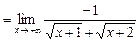
 .
.
 =
= 
 =
= 

 =
= .
.


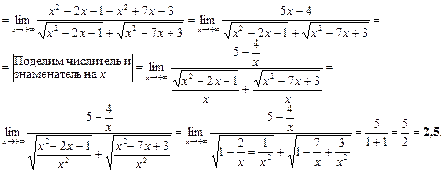
 =
=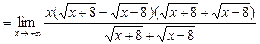
 =
= 
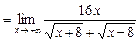
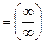 =
= 
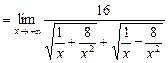
 .
. =
=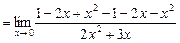 =
= 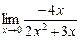

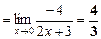 .
.

 .
.


