
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции. Дифференцируемость функции.Содержание книги
Поиск на нашем сайте
Пусть функция
функции
где А - некоторое число, которое не зависит от Для того чтобы функция Если функция дифференцируема в точке dy = y ¢(x 0) Для функции dy = y ¢(x 0) d x, и производная
Основные правила вычисления дифференциалов функций те же, что и для вычисления производной. 1) 2) 3) 4) 5) Функция, дифференцируемая в каждой точке некоторого интервала, называется дифференцируемой на этом интервале. Производная дифференцируемой на интервале функции Связь между непрерывностью и дифференцируемостью. Если функция Обратное заключение неверно: из непрерывности функции в точке Например, функция
Левая и правая производные не равны между собой. Следовательно, в точке Геометрический смысл дифференциала Дифференциал функции в точке
Рис. 4.2
Применение дифференциала функции к приближенным вычислениям. Если приращение
Пример 4.3. Найти дифференциал функции Решение 1) y = Для нахождения дифференциала воспользуемся формулой dy = y ¢(x) d x. Найдем производную заданной функции, применив формулу для нахождения производной произведения:
и правило нахождения производной сложной функции: (f (g (x))' = f ' (g (x))× g ' (x).
Тогда
2) у = dy = y ¢(x) d x – дифференциал функции y(x) Найдем производную заданной функции. Функция у =
Тогда
По формуле для нахождения производной произведения и по правилу дифференцирования сложной функции имеем:
Пример 4.4. Вычислить приближенно с помощью дифференциала 1) Решение 1) Рассмотрим функцию В формуле Найдем значение функции
Тогда имеем: Следовательно, 2) Рассмотрим функцию В формуле Найдем значение функции точке
Тогда имеем: Следовательно,
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

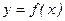 определена в некоторой окрестности точки
определена в некоторой окрестности точки  , а приращение
, а приращение
 в точке
в точке 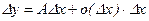 ,
,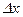 , а
, а  при
при 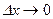 . Тогда функция f(x) называется дифференцируемой в точке
. Тогда функция f(x) называется дифференцируемой в точке  называется ее дифференциалом в точке
называется ее дифференциалом в точке  .
. x.
x. имеем
имеем  , т. е. дифференциал независимого переменного x совпадает с приращением
, т. е. дифференциал независимого переменного x совпадает с приращением  может быть записана как отношение дифференциалов:
может быть записана как отношение дифференциалов: .
. , где c=const.;
, где c=const.; ;
; ;
;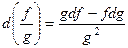 (
(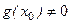 );
); .
. сама является функцией аргумента
сама является функцией аргумента  .
. непрерывна в точке
непрерывна в точке  , но она не дифференцируема в этой точке, т.к.
, но она не дифференцируема в этой точке, т.к.
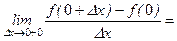
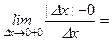
 ,
, 


 .
.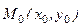 равен приращению ординаты касательной к графику этой функции в точке с абсциссой
равен приращению ординаты касательной к графику этой функции в точке с абсциссой  , при изменении аргумента от
, при изменении аргумента от 
 функции
функции  приближенно равны между собой.
приближенно равны между собой.

 .
. ;2) у =
;2) у = 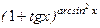 .
.


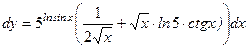 .
.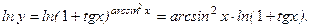
 .
. Тогда
Тогда
 ; 2)
; 2)  .
. .
. ,
,  .
.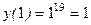 ;
; .
.

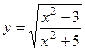 .
. ,
,  .
.
 ;
;

 ;
;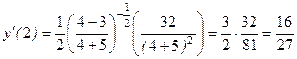

 .
.


