
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функции одного переменного.Содержание книги
Поиск на нашем сайте
Производная функции, ее геометрический смысл.
Пусть функция
Производной функции y = f (x) в точке х 0 называется предел отношения приращения функции Δ f (x 0, Δ x) к соответствующему приращению аргумента Δ x, если приращение аргумента стремится к нулю:
Геометрический смысл производной
Рис.4. 1 Рассмотрим график некоторой функции Значение производной функции f (x) в точке x 0 равно угловому коэффициенту касательной, проведенной к графику функции в этой точке: f ¢(x 0) = k = tg j. Тогда y – f (x 0) = f ¢(x 0)·(x – x 0) – уравнение касательной к графику функции Нормалью к кривой в точке Тогда x – x 0 + f ¢(x 0)·(y – f (x 0)) = 0 – уравнение нормали к графику функции
Основные правила нахождения производных Пусть с = const, v = v (x) и u = u (x) – некоторые функции, дифференцируемые в точке 1) (c)¢ = 0; 2) (x)¢ = 1; 3) (u + v)¢ = u ¢ + v ¢; 4) (u – v)¢ = u ¢ – v ¢; 5) (c u)¢ = c u ¢; 6) 7) (u v)¢ = u ¢ v + u v ¢; 8) 9) Таблица производных основных функций 1) (ха)¢ = a xa– 1; 2) (ax)¢ = ax ln a, 3) 4) (sin x)¢ = cos x; 5) (cos x)¢ = –sin x; 6) (tg x)¢ = 7) (ctg x)¢ = 8) (arcsin x)¢ = 9) (arсcos x)¢ = 10) (arctg x)¢ = 11) (arcctg x)¢ = 12) (log a x)¢ = 13) (sh x)¢ = ch x; 14) (ch x)¢ = sh x; 15) (th x)¢ = Правило дифференцирования сложной функции Если функции z ¢(x 0) = g ¢ (y 0) f ¢(x 0). Правая и левая производная. Правой производной функции
Левой производной функции
Для существования производной
Логарифмическая производная Если функция y = f (x) – дифференцируемая в точке
Функция вида Для дифференцирования степенно-показательной функции
Например, найдем производную от функции
Тогда
Для функции
Тогда
Формулу Например, для нахождения производной от произведения
Пример 4. 1. Найти производные следующих функций: 1) y = – x 4+ x 3+2 х 2+3 x +2 в точке x 0 = – 1; 2) 3) y = 4) y = 5) 7) y = 6 x sin x; 8) y = sin–1(2 x)–log2(2 x –3); 9) 11) y = –log25(– x +2). 12) y = 13) y = 14) y = 15) y = 17) y = Решение а) y = – x 4+ x 3+2 х 2+3 x +2 в точке x 0= – 1. y ' = (– x 4 + x 3 + 2 х 2 + 3 x + 2)' = (– x 4)' + (x 3)' + 2(х 2)' + 3(x)' + 0 = Тогда y '(–1) = –4(–1)3 + 3(–1)2 + 4(–1) + 3 = 4 + 3 – 4 + 3 = 6. б) Преобразуем функцию:
Тогда y ' y '(2) 3) y = Преобразуем функцию
Тогда y ' y' (1) 4) y = y ' = y '(0) 5) Воспользуемся правилом нахождения производной сложной функции: (f (g (x))¢ = f (g (x))¢× g ¢ (x). y ' 6) Воспользуемся правилом нахождения производной сложной функции: (f (g (x))¢ = f ¢ (g (x))× g ¢ (x). y ' 7) y = 6 x sin x. Воспользуемся правилом нахождения производной произведения двух функций: (uv)¢ = u ¢ v + uv ¢. y ' = (6 x)'sin x + 6 x (sin x)' = 6 x ln6 sin x + 6 x cos x. 8) y = sin–1(2 x)–log2(2 x –3). По правилу нахождения производной сложной функции: y ' = (–1)sin–22 x (sin2 x)' – (log2(2 x –3))' = –sin–22 x (cos2 x)(2 x)' – 9) Воспользуемся правилом нахождения производной частного:
10) Преобразуем функцию
Воспользуемся правилом нахождения производной сложной функции: (f (g (x))' = f ' (g (x))× g ' (x). y ' 11) y = –log25(– x +2). Воспользуемся правилом нахождения производной сложной функции: (f (g (x))' = f ' (g (x))× g ' (x).
y ' = –(log25(– x + 2))' = –5log24(– x + 2)(log2(– x + 2))' =
12) y = Воспользуемся правилом нахождения производной сложной функции: (f (g (x))' = f ' (g (x))× g ' (x), а также нечетностью функции
y ' = 13) y = По правилу дифференцирования сложной функции: y ' = 14) y = По правилу дифференцирования сложной функции: y ' = 15) y = По правилу дифференцирования сложной функции:
y ' = 16) y = – x arctg(2 x). y ' = –(x arctg(2 x ))'. Данная функция не является ни показательной, ни степенной. Поэтому для нахождения производной этой функции воспользуемся предварительным логарифмированием: y 1' = y 1(ln y 1)', где у 1 = x arctg(2 x ); ln у 1 = ln x arctg(2 x) = arctg (2 x) ln (x); (ln у 1)' = (arctg (2 x))'ln (x) + arctg (2 x)(ln (x))' =
тогда y ' = – y 1(ln y 1)'= – x arctg(2 x) 17) y = Функция не является ни показательной, ни степенной. Поэтому для нахождения производной этой функции воспользуемся предварительным логарифмированием: ln y = ln
y ' = y (ln y)' = Пример 4.2. Написать уравнение касательной и уравнение нормали к графикам функций Решение 1)Пусть y = y = f (x 0) + f '(x 0)(x – x 0) - уравнение касательной; (x – x 0) + f '(x 0)(y – f (x 0)) = 0 - уравнение нормали. Найдем значение функции в точке х 0=0: f (x 0) = f (0) = Найдем производную функции y = f '(x) = Тогда значение производной в точке х 0=0: f '(x 0) = f '(0) Запишем уравнение касательной: y = Запишем уравнение нормали: (x – 0) + x – Итак, y =
Итак, x – б) у = y = f (x 0) + f '(x 0)(x – x 0) - уравнение касательной; (x – x 0) + f '(x 0)(y – f (x 0)) = 0 - уравнение нормали. Найдем значение функции в точке х 0= -1: f (x 0) = f (-1) = Найдем производную функции у = f '(x) = Тогда значение производной в точке х 0= -1: f '(x 0) = f '(-1) = Запишем уравнение касательной: y =1+2 (x +1) =2 x +3. Запишем уравнение нормали: (x +1)+2 (y –1) = 0; x +1 +2 y -2= 0. Итак, y = 2 x+ 3 – уравнение касательной к графику функции у =
Итак, x +2 y –1 = 0 – уравнение нормали к графику функции у =
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.76.174 (0.006 с.) |

 определена в некоторой окрестности
определена в некоторой окрестности 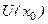 точки
точки  . Тогда для любой точки
. Тогда для любой точки  разность
разность  обозначается
обозначается 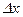 и называется приращением аргумента, соответствующая разность значений функции
и называется приращением аргумента, соответствующая разность значений функции  обозначается
обозначается  и называется приращением функции. Так как
и называется приращением функции. Так как 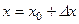 , то
, то 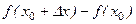 .
.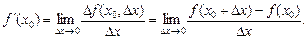

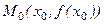 ,
,  - произвольные точки, лежащие на кривой
- произвольные точки, лежащие на кривой 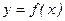 (
(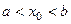 ). Прямая MN называется секущей. Отношение
). Прямая MN называется секущей. Отношение  равно угловому коэффициенту прямой, проходящей через точки M и N. Пусть
равно угловому коэффициенту прямой, проходящей через точки M и N. Пусть 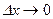 , тогда точка N стремится к точке M. Если существует производная
, тогда точка N стремится к точке M. Если существует производная 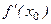 , т.е.существует предел отношения
, т.е.существует предел отношения 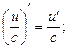
 , v ¹ 0;
, v ¹ 0;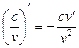 , v ¹ 0.
, v ¹ 0.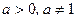 ; (ex)¢ = ex;
; (ex)¢ = ex;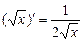 ;
; ;
;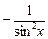 ;
;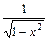 ;
;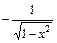 ;
;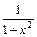 ;
; ;
;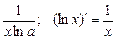 ;
;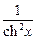 ; 16) (cth x)¢ =
; 16) (cth x)¢ = 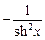 .
. дифференцируемы соответственно в точках
дифференцируемы соответственно в точках 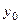 , где y 0 = f (x 0), то сложная функция z = g (f (x)) дифференцируема в точке
, где y 0 = f (x 0), то сложная функция z = g (f (x)) дифференцируема в точке 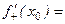
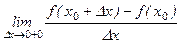 , если указанный предел существует.
, если указанный предел существует.
 , если указанный предел существует.
, если указанный предел существует. функция и
функция и  , то логарифмической производной называется
, то логарифмической производной называется .
. (u(x)>0), где и основание и показатель изменяются вместе с независимой переменной x, называется степенно-показательной. Простейшим примером такой функции является функция
(u(x)>0), где и основание и показатель изменяются вместе с независимой переменной x, называется степенно-показательной. Простейшим примером такой функции является функция 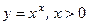 .
.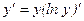 .
. :
: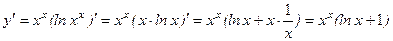 Найти производную функции
Найти производную функции  .
.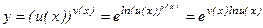 .
.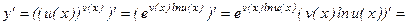
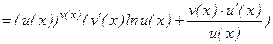 .
.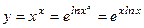 .
.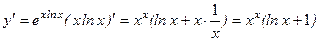 .
. удобно применить логарифмическую производную, что позволит быстрее найти результат. Тогда
удобно применить логарифмическую производную, что позволит быстрее найти результат. Тогда
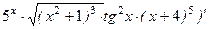 )=
)= 
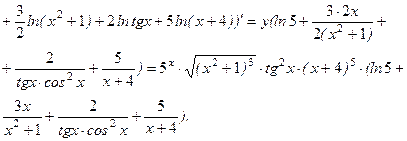
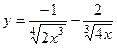 в точке x 0 = 2;
в точке x 0 = 2;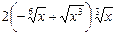 в точке х 0 = 1;
в точке х 0 = 1;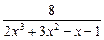 в точке х 0 = 0;
в точке х 0 = 0;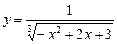 ; 6)
; 6) 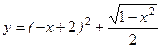 ;
;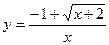 ; 10)
; 10) 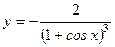 ;
;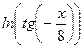 ;
;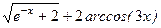 ;
;  ;
;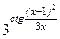 16) y = – x arctg(2 x );
16) y = – x arctg(2 x );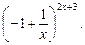


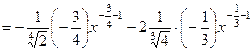 =
=  .
.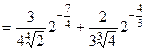
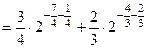
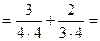
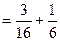
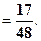

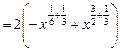
 .
.
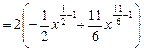

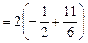

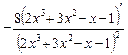
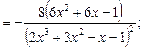
 = 8.
= 8. .
. =
=


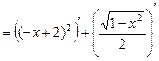
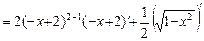 =
=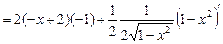

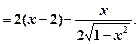
 (2 x –3)' = –2
(2 x –3)' = –2 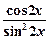 –
– 



 =
= 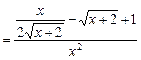
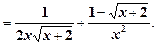


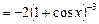 .
.

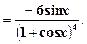
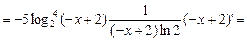

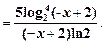
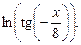
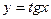 и четностью функции
и четностью функции 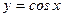 .
.
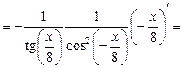

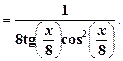


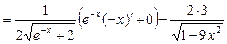

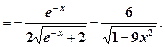

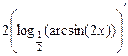
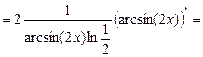

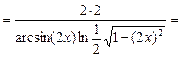
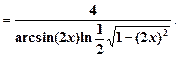
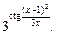

 =
= =
=  =
= 


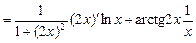

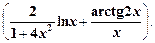


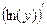

 =
= 

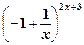

 в точке с абсциссой х 0 = 0;
в точке с абсциссой х 0 = 0; в точке с абсциссой х 0 = -1.
в точке с абсциссой х 0 = -1. .
.

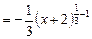
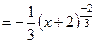
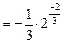
 .
.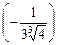 (x – 0).
(x – 0).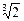 ) = 0;
) = 0; y –
y –  = 0.
= 0. –
– 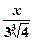 – уравнение касательной к графику функции y =
– уравнение касательной к графику функции y = 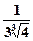 y –
y –  = 0 –уравнение нормали к графику функции y =
= 0 –уравнение нормали к графику функции y = 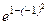 =
= 
 =
= 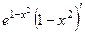 =
= 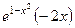 =
=  .
. =
= 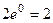 .
.


