
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обробка результатів експертних оцінокСодержание книги
Поиск на нашем сайте Розраховується середнє значення оцінки i-го критерію
Де rik – ранг i - критерій k - експерт
mk – коефіцієнт авторитетності k-го експерта mk Î 0 <mk <1 Далі розраховується дисперсія оцінок:
Потім розраховується варіація цих оцінок
Далі розраховуються вагові коефіцієнти
Ранжирування й зважування, вироблені при ігноруванні правил оперування зі шкальними вимірами, можуть давати настільки ж невірні результати, як, вимір за допомогою гумової стрічки, або ж можуть виявитися настільки ж наївними, як обчислення повного розміру предмета шляхом додавання його маси й обсягу. Якщо не встановлені логічні зв'язки між вимірюваними параметрами, немає способу провести значимі порівняння по єдиній шкалі. Той факт, що фахівці досить часто й успішно використають ці методи, змушує припустити, що ці помилки не завжди настільки великі, щоб спотворити результати. Таким чином, хоча повністю усунути недоліки цих методів і не вдається, можна все-таки виявити необхідну обережність при їхньому використанні. Більшість методів розрахунку страждає подібними недоліками. Він указує, що математично строгі обчислення застосовні тільки для завдань нижчого порядку, а при порівнянні завдань вищого порядку неминуче деяке сполучення обчислень зі здогадами. Як практичне правило можна рекомендувати у всіх випадках, коли є сумніви в застосовності обчислень, просто порівнювати завдання подумки або шляхом обговорення. Інакше не залишається нічого іншого, як засновувати свої судження на суб'єктивних моральних принципах і на вірі (покладаючись, таким чином, на стабільність і непорушність цих принципів при всіх соціально-технічних змінах). Матриця взаємодії Виробляється пошук взаємозв'язків між елементами в рамках однієї системи. При цьому: визначити “елемент” і “взаємозв'язок”; скласти матрицю взаємодій; визначити взаємозв'язок. Матриця взаємодій є одним із самих корисних проектувальних засобів, що виникло в результаті пошуків систематичних методів проектування. Головна перевага цього методу полягає в тому, що він служить засобом виконання суворої, об'єктивної перевірки, нездійсненної чисто уявним шляхом, без допоміжних засобів. Багато спроб систематизувати процес проектування включають використання матриці взаємодій того або іншого виду, і такі матриці використаються також у всіх спробах виразити проектні проблеми у формі, придатної для обробки на ЕОМ. Описані вище порівняно прості дії над матрицею є лише елементарним прикладом застосування загального апарата матричної алгебри. При використанні цього методу виникають наступні труднощі: висока ймовірність помилок при складанні навіть невеликої матриці і її копіюванні. Тому, якщо потрібна висока точність, матрицю повинна перевірити інша людина. тривалий час, необхідне для виконання всіх оцінок, що вимагаються для заповнення матриці, і стомлюючий характер цієї праці, що включає численні консультації. Якщо це дозволяють умови завдання, краще обмежитися матрицею, що містить не більше 20 елементів, або розчленувати завдання так, щоб вийшло кілька невеликих матриць; обмежена цінність матриць, у яких елементи й взаємозв'язки між ними не визначені таким чином, щоб будь-яка людина змогла за тих самих умов виявити ту ж конфігурацію взаємозв'язків; ускладнення, які виникають, якщо елементи не ставляться до того самого рівня ієрархії (тобто якщо якісь елементи насправді становлять частину інших елементів) або якщо не всі елементи належать до того ж сімейства, до якого дійсно застосовні зазначені взаємозв'язки. Діапазон складних проектних ситуацій, у дослідженні яких можна успішно використати матриці, практично необмежений. Важливо вміти розпізнавати ті види невизначеності й складності, які не можна чітко представити в матриці. Матриця взаємодій марна в тих випадках, коли наведені вище правила визначення й вибору елементів незастосовні, тобто коли структуру проблеми не можна з достатнім рівнем точності охарактеризувати за допомогою якої-небудь моделі. Приклад Побудувати матрицю взаємодії для двоколійної тягової ділянки живлення тяговими підстанціями (приймемо, що рівень напруги на шинах однаковий), схема якого наведена на рис. 2.11.
Рисунок 2.11. Схема ділянки
Струм, що виходить із вузла, запишемо зі знаком 1, що входить у вузол - -1, при відсутності такого = 0. Кількість галузей 6 шт., вузлів - 5 шт.
Мережа (граф) взаємодій. Базується на теорії графів. Аналогічно матриці взаємодії, тільки зв'язки будуються в графічному виді (рис. 2.12). Метою побудов є мінімізація перетинань галузей графа.
Рисунок 2.12. Мережа взаємодій Перша робота з теорії графів належить Леонарду Ейлеру (1736 рік), хоча термін «граф» уперше ввів в 1936 році угорський математик Денеш Кеніг. Графами були названі схеми, що складаються із точок, і відрізків, прямих або кривих, які з'єднують ці точки (приклади графів зображені на рис. 2.13).
Рисунок 2.13. Приклади графів За допомогою графів часто спрощувалося рішення завдань, сформульованих у різних областях знань: в автоматиці, електроніці, фізиці, хімії й ін. За допомогою графів зображуються схеми дороги, газопроводів, тепло- і електромережі. Допомагають графи в рішенні математичних і економічних завдань.
Рисунок 2.14. а - Нульовий граф з п'ятьма вершинами, б - Неповний граф з п'ятьма вершинами Точки А, Б, В, Г, Д називаються вершинами графа (рис. 2.14), а відрізки ліній, що з'єднують ці точки — ребрами графа. При зображенні графів на рисунках або схемах, відрізки можуть бути прямолінійної або криволінійними; Довжини відрізків і розташування точок довільні. Наприклад, всі три фігури на рис. 2.15 зображують той самий граф.
Рисунок 2.15. Різні варіанти зображення одного графа Розглянемо процес з'єднання точок А, Б, В, Г, Д ребрами. 1. Точкову схему, зображену на рисунку 2.14 а. Така схема, що складається з «ізольованих» вершин, називається нульовим графом. 2. Графи, у яких не побудовані всі можливі ребра, називаються неповними графами. 3. На рисунку 2.16 зображений граф, який відповідає всім можливим з'єднанням. Цей граф є повним графом. Якщо підрахувати число його ребер, то одержимо 10.
Малюнок 2.16. Повний граф з п'ятьма вершинами Помітимо, що якщо повний граф має n вершин, то кількість ребер буде дорівнює n(n-1)/2 Дійсно, кількість ребер у повному графі з n вершинами визначається як число неупорядкованих пар, складених із всіх n точок-ребер графа, тобто як число сполучень із n елементів по 2. Граф, що не є повним, можна доповнити до повного з тими ж вершинами, додавши відсутні ребра. Так, наприклад, на рисунку 2.14 зображений неповний граф з п'ятьма вершинами. На рисунку 2.16 ребра, які перетворюють граф у повний граф, зображені іншими кольорами, сукупність вершин графа із цими ребрами називається доповненням графа. Ступінь вершини - кількість ребер графа, що виходять із цієї вершини. На рисунку 2.17 зображений граф з п'ятьма вершинами. Ступінь вершини А позначимо Ст.А. На малюнку: Ст.А = 1, Ст.Б = 2, Ст.В = 3, Ст.Г= 2, Ст.Д= 0.
Рисунок 2.17. Ступінь вершини Вершина називається непарною, якщо ступінь цієї вершини непарна, і парною, якщо ступінь цієї вершини парна. Сформулюємо деякі закономірності, властивим певним графам. Закономірність 1. Ступені вершин повного графа однакові, і кожна з них на 1 менше числа вершин цього графа. Закономірність 2. Сума ступенів вершин графа є число парне, рівне подвоєному числу ребер графа. Ця закономірність справедлива не тільки для повного, але й для будь-якого графа. Закономірність 3. Число непарних вершин будь-якого графа парне. Закономірність 4 (випливає з розглянутої нами закономірності 3). Неможливо накреслити граф з непарним числом непарних вершин. Закономірність 5. Якщо всі вершини графа парні, то можна не відриваючи олівець від паперу («одним розчерком»), проводячи по кожному ребру тільки один раз, накреслити цей граф. Рух можна почати з будь-якої вершини й закінчити його в тій же вершині. Закономірність 6. Граф, що має всього дві непарні вершини, можна накреслити, не відриваючи олівець від паперу, при цьому рух потрібно почати з однієї із цих непарних вершин і закінчити в другий з них. Закономірність 7. Граф, що має більше двох непарних вершин, неможливо накреслити «одним розчерком». Фігура (граф), яку можна накреслити, не відриваючи олівець від паперу, називається унікурсальною. Мережі, графи, блок-схеми, потокові схеми й т.ін. - все це способи реалізації загальної угоди про подання зв'язків між елементами у вигляді конфігурації ліній. Єдиною перевагою мережі перед матрицею є легкість сприйняття її структури і з'ясування проблеми. Матриці й мережі - способи вираження однієї й тієї ж системи взаємозв'язків, що доповнюють один одного. Матриця дозволяє послідовно, елемент за елементом відтворити в просторі поза нашим мозком такі структурні моделі, які занадто складні, щоб наш мозок міг охопити їх цілком. Мережа, яка відображає ті ж взаємозв'язки, як тільки вона закінчена й перевірена, дозволяє знову «пересадити» цю структурну модель у наш мозок, звідки надійшли складові її компоненти. Таким чином, наш мозок може використати зовнішні засоби для виявлення структурних моделей у сукупностях елементів інформації, які раніше сприймалися свідомістю тільки ізольовано. Такі структурні моделі занадто важкі для сприйняття в цілісній формі, якщо в них більше 15-20 елементів; тому більші мережі рідко використаються як схеми, що пояснюють структуру проблеми. Як і матриці, мережі знаходять безліч корисних застосувань за умови, що є чіткі визначення елементів і взаємозв'язків між ними.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

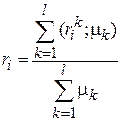
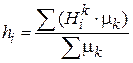

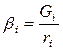






 а)
а)
 б)
б)







