Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Боровская теория водородоподобного атома.⇐ ПредыдущаяСтр 14 из 14
Первый постулат Бора (постулат стационарных состояний): существуют стационарные состояния атома, находясь в которых он не излучает энергию. Этим стационарным состояниям соответствуют вполне определенные (стационарные) орбиты, по которым движутся электроны. При движении по стационарным орбитам электроны, несмотря на наличие у них ускорения, не излучают электромагнитных волн. Правило квантования орбит Бора утверждает, что в стационарном состоянии атома электрона, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию
где m – масса электрона; Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией равной разности энергий соответствующих стационарных состояний:
где Радиус n -й стационарной орбиты:
где а 0 – первый боровский радиус ( Энергия электрона в атоме водорода:
где Энергия, излучаемая или поглощаемая атомом водорода:
или
где n 1 и n 2 – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме. Спектроскопическое волновое число:
где λ – длина волны излучения или поглощения атомом; R – постоянная Ридберга; n 1 и n 2 – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме. Физика твердого тела Средняя энергия квантового одномерного осциллятора:
где Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов:
где R – универсальная газовая постоянная;
Молярная теплоёмкость кристаллического твёрдого тела в области низких температур (предельный закон Дебая):
Теплота, необходимая для нагревания тела:
где m – масса тела; M – молярная масса; T1 и T2 – начальная и конечная температуры тела. Распределение свободных электронов в металле по энергиям при 0 К:
где dn(ε) – концентрация электронов, энергия которых заключена в пределах от ε до ε + d ε; m – масса электрона. Это выражение справедливо при ε < εF (где εF – энергия или уровень Ферми). Энергия Ферми в металле при Т=0 К:
где n - концентрация электронов в металле. Удельная проводимость собственных полупроводников:
где Δ E – ширина запрещённой зоны; γ0 – константа; k – постоянная Больцмана ( Сила тока в p-n – переходе:
где I 0 – предельное значение силы обратного тока; U – внешнее напряжение, приложенное к p-n – переходу; k – постоянная Больцмана ( Внутренняя контактная разность потенциалов:
где
Ядерная физика Ядром называется центральная часть атома, в которой сосредоточены практически вся масса атома и его положительный электрический заряд. Атомное ядро состоит из элементарных частиц – протонов и нейтронов (протонно - нейтронная модель ядра была предложена российским физиком Д. Иваненко, а в последствии развита В. Гейзенбергом). Протоны и нейтроны называются нуклонами. Массовое число ядра (число нуклонов в ядре):
где Z – зарядовое число (число протонов); N – число нейтронов. Энергией связи нуклона в ядре называется физическая величина, равная работе, которую нужно совершить для удаления нуклона из ядра, не сообщая ему кинетической энергии. Энергия связи ядра определяется той работой, которую нужно совершить, чтобы расщепить ядро на составляющие ее нуклоны, не сообщая им кинетической энергии. При образовании ядра происходит уменьшение его массы: масса ядра меньше, чем сумма масс составляющих его нуклонов. Уменьшение массы ядра объясняется выделением энергии связи, то есть
где называется дефектом массы и характеризует уменьшение суммарной массы при образовании ядра из составляющих его нуклонов. Если ядро с массой
где Дефект массы служит мерой энергии связи ядра:
где Во внесистемных единицах энергия связи ядра равна Ядерными реакциями называются превращения атомных ядер, вызванных взаимодействием их друг с другом или с элементарными частицами. В ядерных реакциях участвуют два ядра и две частицы. Одна пара ядро – частица является исходной, другая пара – конечной. Символическая запись ядерной реакции:
где А и В – исходное и конечное ядра; a и b – исходная и конечная частицы в реакции (например: a и b – это такие частицы как α - частица, β - частица, n - нейтрон, p - протон, e+ - позитрон). Ядерная реакция характеризуется энергией Q ядерной реакции, равной разности энергий конечной и исходной пар в реакции. Если Q<0, то реакция идет с поглощением энергии и называется эндотермической; если Q>0, то реакция идет с выделением энергии и называется экзотермической. Закон радиоактивного распада:
где Число ядер, распавшихся за время
В случае, если интервал времени
Зависимость периода полураспада от постоянной радиоактивного распада:
В ядерных реакциях выполняются законы сохранения энергии, импульса, электрического заряда и массовых чисел. Закон сохранения массовых чисел:
Закон сохранения зарядового числа:
При α – распаде распадающее «материнское» ядро испускает α – частицу
Дочерний элемент Y имеет атомный номер на две единицы меньший и, следовательно, сдвинут относительно Х на две клетки влево по таблице Менделеева. При β – распад происходит испускание отрицательно заряженного электрона (то есть β = e)
Уравнения (8.40) и (8.41) носят название правил радиоактивного смещения.
а) электронный β-– распад: ядро испускает электрон и электронное антинейтрино
б) позитронный β+ – распад: ядро испускает позитрон е+ и электронное нейтрино νe, процесс происходит при превращении протона в нейтрон по следующей схеме:
и заключается в том, что исчезает один из электронов на ближайшем к ядру слое. Протон, превращаясь в нейтрон, как бы захватывает электрон. Электронный захват сопровождается характеристическим рентгеновским излучением. 3) γ – излучение Среднее время
Число
где m – масса изотопа; M – молярная масса; Активность A радиоактивного изотопа:
где Удельная активность изотопа:
Примеры решения задач Задача 8.1. Электрон в атоме водорода перешел с четвёртого энергетического уровня на второй. Определить энергию испущенного при этом фотона.
Решение:
Для определения энергии фотона воспользуемся сериальной формулой для водородоподобных ионов (8.20):
где λ – длина волны фотона; R = 3,29·1015 c-1– постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z=1 формула переходит в сериальную формулу для водорода); n 1– номер орбиты, на которую перешел электрон; n 2 – номер орбиты, с которой перешел электрон (n 1 и n 2 – главные квантовые числа). Согласно формуле (8.25), энергия фотона ε равна:
Умножив обе части равенства (1) на hc, получим выражение для энергии фотона:
Так как Rhc есть энергия ионизации E1 атома водорода, то:
Вычисления производим в Международной системе СИ: Ei = 21,76·10-19 Дж
Ответ: ε = Задача 8.2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U 1=51 В; 2) U 2=510 кВ.
Решение:
Длина волны де Бройля согласно формуле (8.2), равна:
Согласно формуле (8.6), имеем (в нерелятивистском случае):
где m 0 – масса покоя частицы. (в релятивистском случае):
где E0 = m0c2 – энергия покоя частицы. Формула (1) с учетом соотношений (2) и (3) (в нерелятивистском случае) имеет вид:
(в релятивистском случае):
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U 1= 51 В и U 2= 510000 В, с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля. Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, равна:
В первом случае, T 1 = e U =
Согласно формуле (8.32),
Во втором случае кинетическая энергия T 2 = eU 2 =
или
Проверим, дает ли полученная формула единицу длины волны (м). Для этого в правую часть формулы (7) вместо величин подставим их единицы:
Вычисления производим в Международной системе единиц СИ:
Ответ:
Задача 8.3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T= 10 эВ. Используя соотношение неопределённостей, оценить минимальные линейные размеры атома.
Решение:
Согласно уравнению (8.7), имеем:
Из соотношения неопределённостей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределённым становится импульс, а следовательно, энергия частицы. Пусть атом имеет линейные размеры l, и тогда электрон атома будет находиться где-то в пределах области с неопределённостью:
С учетом уравнения (2) соотношение неопределённостей (1) имеет вид:
Тогда
Физически разумная неопределённость импульса Δ рх, во всяком случае не должна превышать значения самого импульса рх, т.е.
Проверим, даёт ли полученная (5) формула единицу длины (м). Для этого в правую часть формулы (5) вместо символов величин подставим обозначения их единиц:
Вычисления производим в Международной системе единиц СИ:
Ответ: Задача 8.4. Волновая функция
Так как x изменяется в интервале
С учетом (4) уравнение (3) примет вид:
Так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале (Δ l =0,01 l) практически не изменяется, во втором случае интегрированием можно пренебречь. Поэтому искомая вероятность во втором случае определяется выражением
Вычисления производим в Международной системе единиц СИ:
Ответ: w1 =6,6·10-6, w2 =0,02. Задача 8.5. Вычислить дефект массы и энергию связи ядра
Откуда
Подставляя (2) в уравнение (1), получаем
Учитывая, что
Числовые значения масс находим из таблицы в приложении. В соответствии с законом пропорциональности массы и энергии, согласно формуле (8.24)
Подставляя уравнение (4) в (5), получаем
Вычисления:
Ответ: Δm=0,689 10-28 кг, Wсв =6,201 10-12 Дж.
Задача 8.6. При соударении α-частицы с ядром бора
Решение:
1. Обозначим неизвестное ядро символом
2. Согласно формулам (8.38), (8.39), имеем:
неизвестное ядро является ядром изотопа углерода 3. Тогда реакция имеет вид:
Согласно формуле (8.33), имеем:
Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках - массы ядер – продуктов реакции. При числовых подсчётах по этой формуле массы ядер заменяют массами нейтральных атомов. Возможность 0такой замены вытекает из следующих соображений. Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер – продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода. Вычисления производим в Международной системе единиц:
=
Ответ: Q =
Задача 8.7. Определить начальную активность А0 радиоактивного препарата магния массой m=0,2 мкг, а также его активность A через время t=6 ч. Период полураспада T1/2 магния считать известным.
По закону радиоактивного распада, согласно (8.25), число распадающихся ядер данного сорта N убывает со временем по экспоненциальному закону:
где N0 – начальное число распадающихся атомов при t = 0, λ – постоянная распада. Продифференцируем уравнение (2) по времени:
Поставляя (3) в формулу (1), получаем:
Начальную активность А0 препарата получаем при t=0:
Постоянная радиоактивного распада связана с периодом полураспада Т1/2 соотношением:
Число N0 радиоактивных ядер, содержащихся в изотопе, равно произведению постоянной Авогадро NА на количество вещества данного изотопа:
С учетом выражений (6) и (7) формулы (5) и (4) принимают вид
Вычисления производим в Международной системе единиц СИ:
Ответ: А0=5,13 1012 Бк, А=81,3 Бк.
Задача 8.8. Используя квантовую теорию теплоёмкости Эйнштейна, вычислить удельную теплоёмкость с при постоянном объёме алюминия при температуре Т= 200 К. Характеристическую температуру ΘЕ Эйнштейна принять для алюминия равной 300 К.
Решение:
Формула удельной теплоёмкости c вещества имеет вид:
где М – молярная масса, Согласно формуле (8.23) молярная теплоёмкость при постоянном объёме имеет вид:
Подставим (2) в (1), получим:
Проверим, дает ли полученная формула единицу удельной теплоемкости
Вычисления производим в Международной системе единиц СИ:
Ответ: с = 770 ( Задача 8.9. Определить теплоту Δ Q, необходимую для нагревания кристалла NaCl массой m= 20 г от температуры T 1=2 K до температуры T2 = 4 K. Характеристическую температуру Дебая Θ для NaCl принять равной 320 К и условие T<< ΘD считать выполненным.
Решение: Согласно формуле (8.24) теплота Δ Q, подводимая для нагревания тела от температуры T 1 до T 2, имеет вид:
где С Т – теплоёмкость тела. Теплоёмкость тела связана с молярной теплоёмкостью соотношением:
где m – масса тела; M – молярная масса.
Подставим (2) в (1), получим:
В общем случае теплоёмкость Сm есть сложная функция температуры, поэтому выносить её за знак интеграла нельзя, если выполнено условие T<<ΘD, то Δ Q находим по формуле (8.23), получаем:
Подставим (4) в (3), получим:
Проинтегрировав выражение (5), получим:
Вычисления производим в Международной системе единиц СИ:
Ответ: ΔQ = 1,22 мДж.
Задача 8.10. Вычислить максимальную энергию εF (энергию Ферми), которую могут иметь свободные электроны в металле (медь) при температуре T= 0 К. Принять, что на каждый атом меди приходится по одному валентному электрону.
Решение:
Согласно формуле (8.26) максимальная энергия εF, которую могут иметь электроны в металле при T= 0, имеет вид:
где ħ – постоянная Планка; m – масса электрона.
Концентрация свободных электронов по условию задачи равна концентрации атомов, которая может быть найдена по формуле:
где ρ – плотность меди; NA – постоянная Авогадро; M – молярная масса.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.203.143 (0.246 с.) |
 или
или 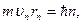
 – скорость электрона на n -й орбите; rn – радиус n- й стационарной орбиты; ħ – постоянная Планка; n – главное квантовое число (n = 1, 2, 3, …).
– скорость электрона на n -й орбите; rn – радиус n- й стационарной орбиты; ħ – постоянная Планка; n – главное квантовое число (n = 1, 2, 3, …).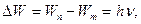
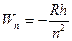 и
и 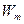 - соответственно энергии стационарных состояний атома до и после излучения (поглощения), где R – постоянная Ридберга (
- соответственно энергии стационарных состояний атома до и после излучения (поглощения), где R – постоянная Ридберга (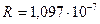
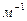 ), n – главное квантовое число.
), n – главное квантовое число.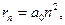
 м).
м).
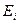 – энергия ионизации атома водорода (
– энергия ионизации атома водорода (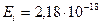 Дж).
Дж).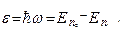

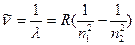
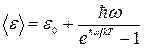 ,
,
 - нулевая энергия (
- нулевая энергия ( );
);  - постоянная Планка;
- постоянная Планка;  - круговая частота колебаний осциллятора; k – постоянная Больцмана (
- круговая частота колебаний осциллятора; k – постоянная Больцмана (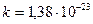 Дж/К); T – абсолютнаятемпература.
Дж/К); T – абсолютнаятемпература.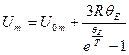
 - характеристическая температура Эйнштейна;
- характеристическая температура Эйнштейна; 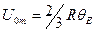 - молярная нулевая энергия (по Эйнштейну).
- молярная нулевая энергия (по Эйнштейну). (
( .
.
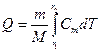 ,
,
 ,
,
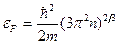 ,
,
 ,
,
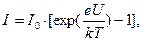
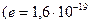 Кл).
Кл).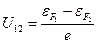 ,
,
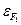 и
и 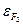 - энергия Ферми соответственно для первого и второго металлов; e – заряд электрона.
- энергия Ферми соответственно для первого и второго металлов; e – заряд электрона.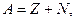

 - энергия связи ядра; с – скорость света в вакууме.
- энергия связи ядра; с – скорость света в вакууме.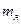 образовано из Z протонов с массой
образовано из Z протонов с массой 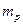 и из (A - Z) нейтронов с массой
и из (A - Z) нейтронов с массой 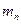 , то дефект массы ядра:
, то дефект массы ядра:
 - зарядовое число (число протонов в ядре);
- зарядовое число (число протонов в ядре); 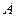 - массовое число (число нуклонов в ядре); (
- массовое число (число нуклонов в ядре); ( ) - число нейтронов в ядре;
) - число нейтронов в ядре; 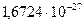 кг);
кг); 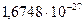 кг);
кг); 
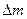 - дефект массы ядра; с – скорость света в вакууме.
- дефект массы ядра; с – скорость света в вакууме.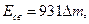 где дефект массы
где дефект массы  ,
,
 или
или 
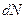 - число ядер, распадающихся за интервал времени
- число ядер, распадающихся за интервал времени 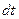 ;
;  - число ядер, не распавшихся к моменту времени
- число ядер, не распавшихся к моменту времени  ;
; 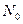 - число ядер в начальный момент (
- число ядер в начальный момент (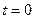 );
); 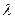 - постоянная радиоактивного распада (
- постоянная радиоактивного распада (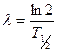 ).
).
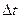 , за который определяется число распавшихся ядер, много меньше периода полураспада
, за который определяется число распавшихся ядер, много меньше периода полураспада 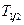 (периодом полураспада называется интервал времени, в течение которого распадается половина ядер), то число распавшихся ядер можно определить по формуле:
(периодом полураспада называется интервал времени, в течение которого распадается половина ядер), то число распавшихся ядер можно определить по формуле: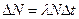 .
.


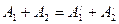
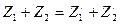
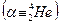 и превращает в «дочернее» ядро элемента Y.
и превращает в «дочернее» ядро элемента Y. .
.
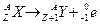 .
.
 ; распад происходит при превращении одного вида нуклона в другой: нейтрона в протон по следующей схеме:
; распад происходит при превращении одного вида нуклона в другой: нейтрона в протон по следующей схеме: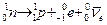 .
.
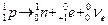 .
.
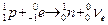 ,
,
 является жестким электромагнитным излучением, энергия которого испускается при переходе ядер из возбужденных энергетических состояний в основное или менее возбужденные состояния, а также при ядерных реакциях.
является жестким электромагнитным излучением, энергия которого испускается при переходе ядер из возбужденных энергетических состояний в основное или менее возбужденные состояния, а также при ядерных реакциях.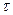 жизни радиоактивного ядра, то есть интервал времени, за который число нераспавшихся ядер уменьшится в е раз:
жизни радиоактивного ядра, то есть интервал времени, за который число нераспавшихся ядер уменьшится в е раз: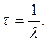
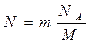 ,
,
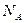 - постоянная Авогадро (
- постоянная Авогадро (
 ).
). или
или 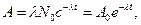
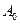 - активность изотопа в начальный момент времени.
- активность изотопа в начальный момент времени.

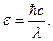

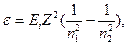
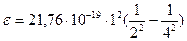 =
= 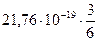 =
=  Дж.
Дж. =?
=?
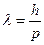 , (1)
, (1)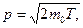
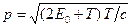 ,
,
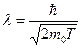
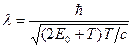 .
.
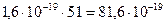 Дж, что много меньше энергии покоя электрона E0 = m0·c2 =
Дж, что много меньше энергии покоя электрона E0 = m0·c2 = 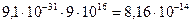 Дж. Следовательно, в этом случае можно применить формулу (4). Так как T 1=10-4 · m0c2,, тогда выражение (4), имеет вид:
Дж. Следовательно, в этом случае можно применить формулу (4). Так как T 1=10-4 · m0c2,, тогда выражение (4), имеет вид: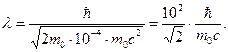
 есть комптоновская длина волны, тогда выражение (7), имеет вид:
есть комптоновская длина волны, тогда выражение (7), имеет вид:
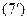
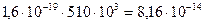 Дж, то есть равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5).
Дж, то есть равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5).
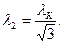
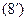

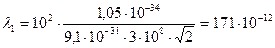 м = 171 пм;
м = 171 пм;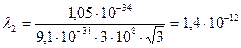 м = 1,4 пм.
м = 1,4 пм.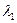 = 171 пм;
= 171 пм;  = 1,4 пм.
= 1,4 пм.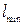 =?
=?
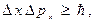 (1)
(1)
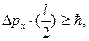

 Согласно (8.6), имеем:
Согласно (8.6), имеем: 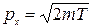 . Заменим Δ рх значением
. Заменим Δ рх значением 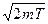 (такая замена не увеличит l). Переходя в уравнении (4) от неравенства к равенству, получим:
(такая замена не увеличит l). Переходя в уравнении (4) от неравенства к равенству, получим: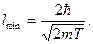
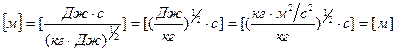
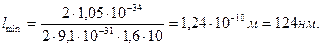
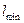 = 124 нм.
= 124 нм.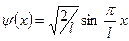 описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Δ l =0,01 l в двух случаях: 1) вблизи стенки
описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Δ l =0,01 l в двух случаях: 1) вблизи стенки 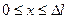 ; 2) в средней части ящика
; 2) в средней части ящика  .
.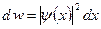 (2)
(2)
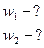
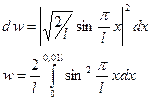
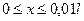 и, следовательно,
и, следовательно,  , справедливо приближенное равенство
, справедливо приближенное равенство 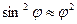 , т.е.
, т.е. .
.

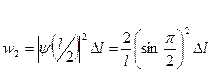
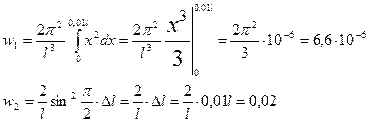
 .
.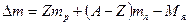 .
.
 .
.
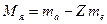 .
.
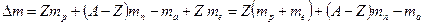
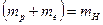 , где mH – масса атома водорода, находим
, где mH – масса атома водорода, находим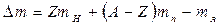
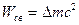 .
.


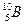 произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода  . Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить её энергетический эффект.
. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить её энергетический эффект.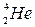 ,
,
 ,
,
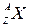 =?
Q =?
=?
Q =?
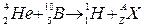 (1)
(1)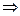 А = 13,
2 + 5 1 + Z
А = 13,
2 + 5 1 + Z 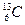 .
.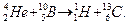
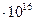
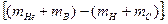
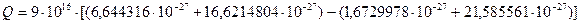 =
=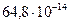 Дж.
Дж.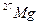

 ,
,
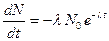 .
.
 .
.
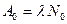 .
.
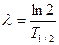 .
.
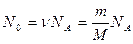 .
.
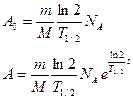

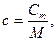
 - молярная теплоемкость.
- молярная теплоемкость.

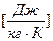 , для этого в правую часть формулы (3) вместо величин подставим их единицы.
, для этого в правую часть формулы (3) вместо величин подставим их единицы.
 =770 (
=770 ( ).
).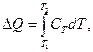 (1)
(1)
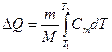 .
.
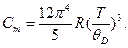
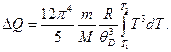
 =
= 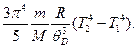
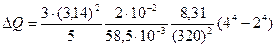 Дж =
Дж = 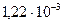 Дж = 1,22 мДж.
Дж = 1,22 мДж.