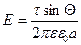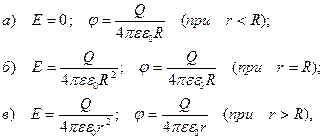Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность поля между пластинами конденсатора
где U – разность потенциалов между пластинами конденсатора, d – расстояние между ними. Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь – система двух равных по модулю разноименных зарядов (+Q, - Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда q на плечо l, называется дипольным электрическим моментом
Величина дипольного момента в первом приближении прямо пропорциональна приложенному полю E. Число силовых линий, пронизывающих элементарную площадку dS, нормаль n которой составляет угол α с вектором Е, определяет поток вектора электрической напряженности, т.е.
где En – проекция вектора напряженности Е на нормаль n к площадке dS (рис. 4.3). Для произвольной замкнутой поверхности S, поток вектора напряженности
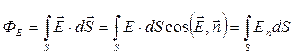 (4.11) (4.11)
Поток вектора напряженности зависит только от алгебраической суммы зарядов, охватываемых этой поверхностью, т.е.
Выражение (4.12) составляет суть теоремы Гаусса: поток вектора Скачкообразное изменение вектора напряженности электрического поля и числа линий напряженности на границе диэлектриков создает ряд неудобств при расчете электрических полей. Поэтому вводят вспомогательное поле
Вектор По теореме Гаусса поток вектора электрического смещения через любую замкнутую поверхность численно равен алгебраической сумме находящихся внутри этой поверхности зарядов
Между потоком вектора электрического смещения и числом силовых линий напряженности имеется числовое равенство
где ρ – объемная плотность зарядов, V – объем, в котором заключен заряд.
Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя теорему Гаусса (4.15), определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность. Рассмотрим примеры расчета электростатических полей в вакууме с использованием теоремы Гаусса. Равномерно заряженная бесконечная плоскость создает однородное электростатическое, модуль напряженности которого равен
где σ – поверхностная плотность зарядов, ε – диэлектрическая проницаемость среды, ε0 – электрическая постоянная. Две равномерно, с одинаковой поверхностной плотностью, и разноименно заряженные бесконечные параллельные плоскости (например, плоский конденсатор) создают однородное электростатическое поле в пространстве между плоскостями с напряженностью, модуль которого равен
Если плоскость представляет собой диск радиусом R, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из центра диска на расстоянии а от нее
Напряженность поля, образованного заряженной бесконечно длинной нитью (или цилиндром)
где τ – линейная плотность заряда на нити, a – расстояние от нити до заряда. Если нить имеет конечную длину, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из середины нити на расстоянии а от нее,
где Θ – угол между направлением нормали к нити и радиус – вектором, проведенным из рассматриваемой точки к концу нити. Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы
где Q – заряд сферы.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1891; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.81.240 (0.006 с.) |
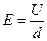 ,
,
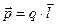 ,
,
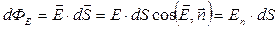 , (4.10)
, (4.10)
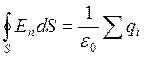 (4.12)
(4.12)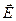 сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на электрическую постоянную
сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на электрическую постоянную 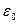 .
.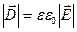 . (4.13)
. (4.13)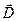 , равный произведению вектора напряженности
, равный произведению вектора напряженности 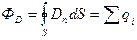 . (4.14)
. (4.14)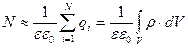 , (4.15)
, (4.15)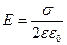 ,
,
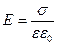 .
.
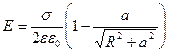
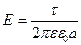 ,
,