
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовая механика. Основы атомной и ядерной физики
Основные формулы и понятия Квантовая механика Французский физик Луи де Бройль пришел к выводу, что корпускулярно-волновая двойственность свойств характерна не только для света. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс
где h = 6,62 10-34 Дж · с – постоянная Планка. Соотношения (8.1) постулировалось не только для фотонов, но и для других микрочастиц (например, электрон, протон, мюзон и т.д. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:
Длина волны для частицы с массой m, движущейся со скоростью υ <<c,
Если частица имеет кинетическую энергию W, то длина волны
Формула де Бройля экспериментально подтвердилась в экспериментах К. Дэвиссона и Л. Джермера, наблюдавших рассеяние электронов монокристаллов никеля. Соотношением, углубляющим представление о корпускулярно-волновой двойственности свойств частиц, является перенесенная на эти частицы связь между энергией W свободной частицы и частотой ν волн де Бройля:
где Импульс частицы и его связь с кинетической энергией Т:
где m 0 – масса покоя частицы; m – релятивистская масса; υ – скорость частицы; с – скорость света в вакууме ( Соотношение неопределённостей: Для координаты и импульса:
где Для энергии и времени:
где Одномерное уравнение Шредингера для стационарных состояний:
где
Плотность вероятности:
где Вероятность обнаружения частицы в интервале от
Решение уравнения Шредингера для бесконечно глубокой одномерной потенциальной ямы.
Рис 8.1. Потенциальная энергия частицы, находящейся в бесконечно глубокой одномерной потенциальной яме
Собственная нормированная волновая функция:
Собственное значение энергии:
где Атомная физика
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.60.35 (0.008 с.) |
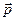 , а с другой стороны – волновые характеристики – частота ν и длина волны λ. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:
, а с другой стороны – волновые характеристики – частота ν и длина волны λ. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов: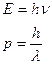 ,
,
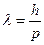 .
.
 .
.
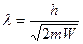 .
.
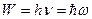 ,
,
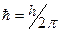 , ω – циклическая частота. Под свободной частицей понимается частица, движущаяся по инерции в отсутствие внешнего силового поля.
, ω – циклическая частота. Под свободной частицей понимается частица, движущаяся по инерции в отсутствие внешнего силового поля.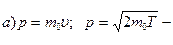 для нерелятивистской частицы;
(8.6)
для нерелятивистской частицы;
(8.6)
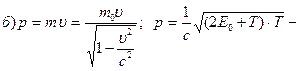 для релятивистской частицы
для релятивистской частицы
 м/с); E 0 – энергия покоя частицы (
м/с); E 0 – энергия покоя частицы ( ).
).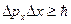 ,
,
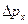 - неопределенность проекции импульса на ось ОX;
- неопределенность проекции импульса на ось ОX; 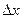 - неопределённость координаты.
- неопределённость координаты. ,
,
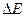 – неопределённость энергии;
– неопределённость энергии; 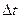 – время жизни квантовой системы в данном энергетическом состоянии.
– время жизни квантовой системы в данном энергетическом состоянии.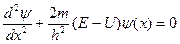 ,
,
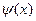 - волновая функция, описывающая состояние частицы; m – масса частицы; Е – полная энергия;
- волновая функция, описывающая состояние частицы; m – масса частицы; Е – полная энергия; 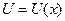 - потенциальная энергия частицы.
- потенциальная энергия частицы.
 - вероятность того, что частица может быть обнаружена вблизи точки с координатой
- вероятность того, что частица может быть обнаружена вблизи точки с координатой  на участке
на участке 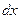 .
. до
до 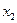 :
: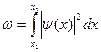
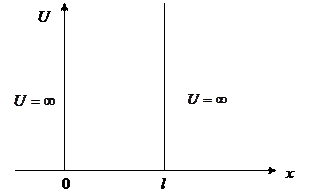

 ,
,
 - квантовое число (
- квантовое число ( 1, 2, 3, …);
1, 2, 3, …); 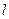 - ширина ямы. В области
- ширина ямы. В области 
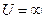 и
и  .
.


