
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Период колебаний пружинного маятника
где k – коэффициент упругости тела, m - масса груза Математическим маятником называется система, состоящая из материальной точки массой m, подвешенной на невесомой нерастяжимой нити, совершающей колебания под действием силы тяжести (рис.5.13,б). Период колебаний математического маятника
где l – длина математического маятника, g – ускорение свободного падения. Физическим маятником называется твердое тело, которое совершает колебания под действием силы тяжести вокруг горизонтальной оси подвеса, не проходящей через центр масс тела (рис.5.13,в).
где J – момент инерции колеблющегося тела относительно оси колебаний; d – расстояние центра масс маятника от оси колебаний; При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой
Результирующая начальная фаза, получаемая при сложении двух колебаний, определяется следующим соотношением:
где A1 и A2 – амплитуды слагаемых колебаний, φ1 и φ2 – их начальные фазы. При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего движения имеет вид:
Если на материальную точку, кроме упругой силы действует сила трения, то колебания будут затухающими, и уравнение такого колебания будет иметь вид
где Логарифмическим декрементом затухания называется отношение двух амплитуд, отстоящих друг от друга по времени, равным периоду
Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины периодически меняются и сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – цепь, состоящая из включенных последовательно катушки индуктивности L, конденсатора емкостью C и резистора сопротивлением R (рис.5.14). Период T электромагнитных колебаний в колебательном контуре
Если сопротивление колебательного контура мало, т.е.
Если сопротивление контура R не равно нулю, то колебания будут затухающими. При этом разность потенциалов на обкладках конденсатора меняется со временем по закону
где δ – коэффициент затухания, U0 – амплитудное значение напряжения. Коэффициент затухания колебаний в колебательном контуре
где L – индуктивность контура, R – сопротивление. Логарифмическим декрементом затухания называется отношение двух амплитуд, отстоящих друг от друга по времени, равное периоду
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы ω к частоте, равной или близкой собственной частоте ω0 колебательной системы (рис.5.15.). Условие получения резонанса:
Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшится в e раз, называется временем релаксации
Для характеристики затухания колебательных контуров часто пользуются величиной, называемой добротностью контура. Добротностью контура Q называется число полных колебаний N, умноженное на число π, по истечению которых амплитуда уменьшается в e раз
Если коэффициент затухания равен нулю, то колебания будут незатухающими, напряжение будет меняться по закону
В случае постоянного тока отношение напряжения к силе тока называют сопротивлением проводника. Подобно этому при переменном токе отношение амплитуды активной составляющей напряжения U а к амплитуде тока i0 называется активным сопротивлением цепи X
В рассматриваемой цепи оно равно сопротивлению постоянного тока. Активное сопротивление всегда приводит к выделению тепла. Отношение
называется реактивным сопротивлением цепи. Наличие реактивного сопротивления в цепи не сопровождается выделением тепла. Полным сопротивлением называется геометрическая сумма активного и реактивного сопротивления
Емкостным сопротивлением цепи переменного тока Xc называется соотношение
Индуктивное сопротивление
Закон Ома для переменного тока записывается в виде
где Iэф и Uэф – эффективные значения силы тока и напряжения, связанные с их амплитудными значениями I0 и U0 соотношениями
Если цепь содержит активное сопротивление R, емкость C и индуктивность L, соединенные последовательно, то cдвиг фаз между напряжением и силой тока определяется формулой
Если активное сопротивление R и индуктивность включены параллельно в цепь переменного тока, то полное сопротивление цепи определяется формулой
и сдвиг фаз между напряжением и током определяется следующим соотношением
где υ – частота колебаний. Мощность переменного тока определяется следующим соотношением
Длина волны связана с периодом следующим соотношением
где c=3·108м/с – скорость распространения звука.
Примеры решения задач Задача 5.1. По отрезку прямого провода длиной l = 80 см течет ток I = 50 А. Определить магнитную индукцию B поля, создаваемого этим током, в точке А, равноудаленной от концов отрезка провода и находящейся на расстоянии r0 = 30 см от его середины.
где символ l означает, что интегрирование распространяется на всю длину провода.
Запишем закон Био - Савара – Лапласа для индукции магнитного поля в векторной форме:
где dB – магнитная индукция, создаваемая элементом провода длиной d l с током I в точке, определяемой радиус-вектором r; μ0 – магнитная постоянная, μ – магнитная проницаемость среды, в которой находится провод (в нашем случае, т.к. средой является воздух, μ = 1). Векторы
где dB определяется выражением (2), которое в скалярной форме имеет вид:
где α – угол между радиус-вектором Подставляя выражение (4) в (3), получим
Из рисунка найдем:
С учетом этого уравнение (5) примет вид:
где α1, α2 – пределы интегрирования. Проинтегрировав выражение (5), получим
Заметим, что при симметричном расположении точки А относительно отрезка провода cos α2 = - cos α1. С учетом этого формула (7) примет вид
Из рисунка следует, что
Подставляя формулу (9) в (8), получим
Проверим, дает ли правая часть полученного равенства единицу индукции магнитного поля (Тл)
Вычисления:
Ответ: B = 26,7·10-6 Тл.
Задача 5.2. Два параллельных бесконечно длинных провода D и C, по которым текут токи в одном направлении электрические токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию  поля, создаваемого проводниками с током в точке А (рис.), отстоящей от оси одного проводника на расстоянии r1 = 5 см, от другого – r2 = 12 см. поля, создаваемого проводниками с током в точке А (рис.), отстоящей от оси одного проводника на расстоянии r1 = 5 см, от другого – r2 = 12 см.
Модуль вектора магнитной индукции найдем по теореме косинусов:
где α – угол между векторами B1 и B2. Магнитные индукции B1 и B2 выражаются соответственно через силу тока I и расстояния r1 и r2 от проводов до точки А:
Поставляя выражение (2) в (1), и вынося
Из рисунка видно, что α = Ð DAC (как углы с соответственно перпендикулярными сторонами). Из треугольника DAC по теореме косинусов, найдем cosα
Подставляя выражение (4) в (3), получим
Проверим, дает ли правая часть полученного равенства единицу индукции магнитного поля (Тл)
Вычисления:
Ответ: B = 3,08·10-4 Тл.
Задача 5.3. По тонкому проводящему кольцу радиусом R = 10 см течет ток I = 80 А. Найти магнитную индукцию
определяемой радиус-вектором
Выделим на кольце элемент dl и от него в точку А проведем радиус-вектор r (рис). Вектор dB направим в соответствии с правилом буравчика. Согласно принципу суперпозиции магнитных полей (5.3), магнитная индукция B в точке А определяется интегрированием
где интегрирование ведется по всем элементам d l кольца. Разложим вектор dB на две составляющие dB┴, перпендикулярную плоскости кольца, и dB ||, параллельную плоскости кольца, т.е.
Подставляя выражение (2) в (1), получим
Заметив, что
где С учетом этого формула (3) примет вид
Из рисунка видно, что Следовательно, формула (4) примет вид
Проверим, дает ли правая часть равенства (5) единицу магнитной индукции
Вычисления:
Ответ: B = 6,28·10-5 Тл. Задача 5.4. Длинный провод с током I = 50 А изогнут под углом α = 2π/3. Определить магнитную индукцию
Из закона Био-Савара-Лапласа следует, что в точках, лежащих на оси провода, магнитная индукция dB=0 (т.к. Следовательно, магнитная индукция B2 = 0. Согласно формуле (5.9), магнитная индукция B1 определяется соотношением
где r0 – кратчайшее расстояние от провода 1 до точки А (рис. к задаче 5.4., б). В нашем случае, т.к. провод длинный α1→0, α2 = α = 2π/3 (cosα2 = cos(2π/3) = - 1/2). Из рисунка следует, что С учетом этого формула (1) примет вид
Проверим, дает ли правая часть полученного равенства единицу магнитной индукции (Тл):
Вектор Вычисления:
Ответ: B = 3,46·10-5 Тл.
Задача 5.5. Два бесконечно длинных провода скрещены под прямым углом (рис. к задаче 5.5., а). По проводам текут токи I1 = 80 А и I2 = 60 А. Расстояние d между проводами равно 10 см. Определить магнитную индукцию B в точке А, одинаково удаленной от обоих проводов.
Из рисунка следует, что векторы B1 и B2 взаимно перпендикулярны (их направления находятся по правилу буравчика и изображены в двух проекциях на рис. к задаче 5.5.,б).
Тогда модуль вектора B можно определить по теореме Пифагора:
Напряженность магнитного поля, согласно (5.8), созданного бесконечно длинным прямолинейным проводником,
где r – расстояние от точки, где находится напряженность, до проводника с током. Согласно формуле (5.6), магнитная индукция B связана с напряженностью H магнитного поля соотношением
где μ – относительная магнитная проницаемость среды (в нашем случае μ = 1). Подставляя формулу (2) в (3), найдем магнитные индукций B1 и B2, создаваемых токами I1 и I2
По условию задачи, r0 = d/2. С учетом этого выражение (4) примет вид
Подставляя формулу (4) в (1), получим
Проверим, дает ли правая часть полученного равенства единицу магнитной индукции (Тл):
Вычисления:
Ответ: B = 4·10-6 Тл.
Задача 5.6. Бесконечно длинный провод изогнут так, как это изображено на рисунке к задаче 5.6, а. Радиус R дуги окружности равен 10 см. Определить магнитную индукцию
В нашем случае провод можно разбить на три части (рис. к задаче 5.6, б): два прямолинейных провода (1 и 3), одним концом, уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
где Так как точка О лежит на оси провода 1, то С учетом этого, уравнение (1) примет вид:
Учитывая, что векторы
Магнитную индукцию B2 найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока:
В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому
Магнитную индукцию B3 найдем, воспользовавшись соотношением (5.9):
В нашем случае r0 = R, α1 = π/2 (cos α1 = 0), α2 → π (cos α2 = -1). Тогда
Подставляя формулы (4), (6) в (3), получим
или
Проверим, дает ли правая часть полученного равенства единицу магнитной индукции (Тл):
Вычисления:
Ответ: B = 3,31·10-4 Тл.
Задача 5.7. По двум параллельным прямым проводам длиной l = 2,5 см каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.
Ток I1 создает в месте расположения второго провода (с током I2) магнитное поле. Проведем линию магнитной индукции (пунктир на рис.) через второй провод и по касательной к ней – вектор магнитной индукции B1.
Рисунок к задаче 5.7
Модуль магнитной индукции B1 определяется соотношением
Согласно закону Ампера (5.4), на каждый элемент второго провода с током I2 длиной d l действует в магнитном поле сила
Так как вектор d l перпендикулярен вектору B1, то sin(d l,B) = 1 и тогда
Подставив выражение (1) в (2), получим
Силу F взаимодействия проводов с током найдем интегрированием:
Так как I1 = I2 = I, получим
Проверим, дает ли правая часть полученного равенства единицу силы (Н):
Вычисление:
Ответ: F = 2,5 Н.
Задача 5.8. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией B = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.
Так как сила Лоренца перпендикулярна вектору скорости Согласно второму закону Ньютона,
где m – масса протона. На рисунке совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора Запишем выражение (1) в скалярной форме (в проекции на радиус):
Согласно формуле (5.19), сила Лоренца в скалярной форме имеет вид
С учетом того, что
Нормальное ускорение
Подставляя выражения (4) и (5) в (2), получим
Следовательно, радиус окружности
Заметив, что m
Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. A = ΔT, или
где φ1 – φ2 = U– ускоряющая разность потенциалов; T1, T2 – начальная и конечная кинетическая энергии протона. Пренебрегая начальной кинетической энергией протона (T1 = 0) и выразив кинетическую энергию T2 через импульс p, получим
Откуда
Подставляя выражение (8) в (7), получим
Убедимся, что правая часть полученного равенства дает единицу длины (м):
Вычисления:
Ответ: R = 0,0118 м.
Задача 5.9. Электрон движется в однородном магнитном поле (B = 10 мТл) по винтовой линии, радиус r которой равен 1 см и шаг h = 6 см. Определить период T обращения электрона и его скорость  . .
Скорость Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью Согласно формуле (5.20), период обращения электрона в магнитном поле
Согласно второму закону Ньютона
Согласно формуле (5.19), сила Лоренца в скалярной форме имеет вид
С учетом того, что sinα = 1, получим
Нормальное ускорение
Подставляя выражения (4) и (3) в (2), получим
Следовательно, скорость электрона
Подставляя полученное выражение в формулу (1), получим
Модуль скорости электрона
Параллельную составляющую скорости
Подставляя выражение (6) в (8), получим
Таким образом, модуль скорости электрона
Убедимся в том, что правая часть равенств (6) и (9) дает единицы времени (с) и скорости (м/с) соответственно:
Вычисления:
Ответ: T = 3,57·10-9 с, Задача 5.10. Альфа – частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое (E = 10 кВ/м) и магнитное (B = 0,1 Тл) поля. Найти отношение заряда альфа - частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.30.162 (0.341 с.) |
 , (5.47)
, (5.47) , (5.48)
, (5.48) ,
, - приведенная длина физического маятника.
- приведенная длина физического маятника. . (5.49)
. (5.49) , (5.50)
, (5.50) . (5.51)
. (5.51) , (5.52)
, (5.52) называется коэффициентом затухания (r – коэффициент сопротивления).
называется коэффициентом затухания (r – коэффициент сопротивления). . (5.53)
. (5.53)
 . (5.54)
. (5.54) <<1/LC, то период колебаний колебательного контура определяется формулой Томсона
<<1/LC, то период колебаний колебательного контура определяется формулой Томсона . (5.55)
. (5.55) , (5.56)
, (5.56) , (5.57)
, (5.57) . (5.58)
. (5.58)
 . (5.59)
. (5.59) . (5.60)
. (5.60) . (5.61)
. (5.61) . (5.62)
. (5.62) . (5.63)
. (5.63) . (5.64)
. (5.64) , (5.65)
, (5.65) . (5.66)
. (5.66) . (5.67)
. (5.67) , (5.68)
, (5.68) и
и  . (5.69)
. (5.69)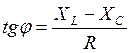 . (5.70)
. (5.70) , (5.71)
, (5.71) , (5.72)
, (5.72) . (5.73)
. (5.73)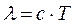 , (5.74)
, (5.74) , (1)
, (1)




 ,
,
 от различных элементов тока сонаправлены (рис.), поэтому выражение (1) можно переписать в скалярной форме:
от различных элементов тока сонаправлены (рис.), поэтому выражение (1) можно переписать в скалярной форме: ,
,
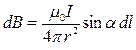 ,
,
 и элементом тока dl.
и элементом тока dl. .
.
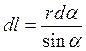 , где
, где  .
. ,
,
 .
.




 Тл.
Тл.

 , (1)
, (1)
 за знак корня, получим
за знак корня, получим .
.

 .
.

 Тл
Тл .
.
 ,
,

 .
. из соображений симметрии и что векторы
из соображений симметрии и что векторы  от различных элементов d l сонаправлены, заменим векторное суммирование (интегрированием) скалярным:
от различных элементов d l сонаправлены, заменим векторное суммирование (интегрированием) скалярным: ,
,
 и
и  (поскольку d l перпендикулярен r и, следовательно, sinα = 1).
(поскольку d l перпендикулярен r и, следовательно, sinα = 1). .
.
 .
.

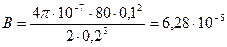 Тл.
Тл.
 и
и  полей, создаваемых отрезками 1 и 2
полей, создаваемых отрезками 1 и 2
 .
.
 ).
). ,
,

 .
.

 Тл.
Тл.




 ,
,
 ,
,
 и
и 
 и
и 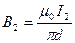

 Тл.
Тл.

 .
.
 ,
,
 - магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.
- магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода. .
.
 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим:
направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим:
 .
.
 .
.

 .
.



 Тл.
Тл.
 .
.






 Н.
Н.
 .
.
 , то она сообщит частице (протону) нормальное ускорение a n.
, то она сообщит частице (протону) нормальное ускорение a n. ,
,
 . Силу Лоренца направим перпендикулярно вектору
. Силу Лоренца направим перпендикулярно вектору  к центру окружности (векторы a n и Fл сонаправлены). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора
к центру окружности (векторы a n и Fл сонаправлены). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора  ).
). .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 есть импульс протона (p), выражение (6) можно записать в виде:
есть импульс протона (p), выражение (6) можно записать в виде: .
.
 ,
,
 .
.
 .
.
 .
.

 м.
м.
 электрона на две составляющие: параллельную вектору B (
электрона на две составляющие: параллельную вектору B ( ) и перпендикулярную ему (
) и перпендикулярную ему ( ).
).
 в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль силовой линии. Скорость
в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль силовой линии. Скорость  в результате действия силы Лоренца будет изменяться только по направлению (
в результате действия силы Лоренца будет изменяться только по направлению ( ) (в отсутствие параллельной составляющей (
) (в отсутствие параллельной составляющей ( = 0) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям).
= 0) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям). и равномерном движении по окружности со скоростью
и равномерном движении по окружности со скоростью  .
.
 .
.
 .
.
 .
.
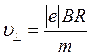 .
.


 , откуда
, откуда


 .
.

 .
. с.
с. м/с
м/с = 2,46·107 м/с.
= 2,46·107 м/с.



