
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент полезного действия цепи
где Аст – работа сторонних сил.
Примеры решения задач Задача 4.1. Три точечных заряда Q1=Q2=Q3=1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?
Заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (см. рис.):
где F2, F3, F4 – силы, с которыми соответственно действуют на заряд Q1 заряды Q2, Q3, Q4; F – равнодействующая сил F2 и F3. Так как силы F и F4 направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным:
F - F4 = 0,
Откуда F = F4. Согласно рисунку Следовательно, модуль силы F4
т.к. F2 = F3 По закону Кулона, согласно уравнению (4.1.)
Подставляя уравнения (3) в формулу (2), с учетом того, что Q1=Q2=Q3, получим
откуда
Из геометрических построений в равностороннем треугольнике следует, что
С учетом этого формула (4) примет вид
Вычисления:
Ответ: Q4 = 5,77 · 10-10 Кл.
Задача 4.2. Два шарика одинаковых радиусов и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд нужно сообщить шарикам, чтобы сила натяжения стала равной 98 мН? Расстояние от центра шарика до точки подвеса 10 см, масса каждого шарика 5г.
Спроецируем уравнение (1) на оси OX и OY: Ось OX:
Ось OY:
По закону Кулона, согласно уравнению (3.1):
т.к. по условию, поверхности шариков соприкасаются, то заряд, полученный шариками, распределится поровну, и заряд каждого шарика будет равен q/2. Следовательно, уравнение (4) можно записать в следующем виде:
Из основного тригонометрического тождества:
Из рисунка видно, что
Решая полученную систему уравнений относительно искомой величины:
можно получить:
Проверим, дает ли правая часть равенства (8) единицу заряда (Кл):
Вычисления производим в Международной системе СИ:
Ответ:
Задача 4.3. На тонком стержне длиной l = 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня, на расстоянии a = 10 см от ближайшего конца находится точечный заряд Q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне.
Выделим на стержне (см. рис) малый участок dr с зарядом
Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,
Интегрируя выражение (2) в пределах от a до a+l, получаем
откуда
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:
Найденная единица является единицей линейной плотности заряда. Вычисления:
Ответ: τ=2,5·10-9 Кл/м. Задача 4.4. Два точечных электрических заряда Q1 = 1 нКл и Q2 = - 2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Определить напряженность E и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1 на расстоянии r1 = 9 см и от заряда Q2 на r2 = 7 см.
Вектор
Модуль вектора E найдем по теореме косинусов:
где α – угол между векторами
В данном случае во избежание громоздких записей удобно значение cosα вычислить отдельно:
Подставляя выражение (2) в (3) и вынося общий множитель 1/(4πε0) за знак корня, получаем
Потенциал результирующего поля, создаваемого двумя зарядами Q1 и Q2, согласно формуле (4.27)
Потенциал поля точечного заряда Q, находящегося в точке на расстоянии r от него, согласно (4.26)
Соответственно потенциал поля для зарядов Q1 и Q2 :
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.112.1 (0.086 с.) |
 ,
,


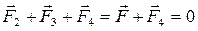 (1)
(1) ,
, , (2)
, (2) . (3)
. (3)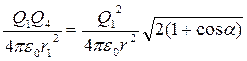 ,
, . (4)
. (4) .
.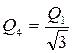 .
.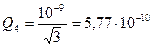 Кл
Кл (1)
(1)
 (2)
(2)
 (3)
(3) , (4)
, (4) . (5)
. (5)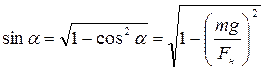 . (6)
. (6) (7)
(7)
 (8)
(8)

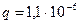 Кл.
Кл.
 . (1)
. (1)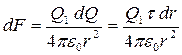 . (2)
. (2)
 .
.
 Кл/м
Кл/м . (1)
Напряженности Е1 и Е2 полей, создаваемых каждым зарядом Q 1 и Q 2 в отдельности:
. (1)
Напряженности Е1 и Е2 полей, создаваемых каждым зарядом Q 1 и Q 2 в отдельности:
 (2)
(2)
 (см. рис) направлен по силовой линии от заряда Q1, так как этот заряд положителен; вектор
(см. рис) направлен по силовой линии от заряда Q1, так как этот заряд положителен; вектор  направлен также по силовой линии, но к заряду Q2, так как этот заряд отрицателен.
направлен также по силовой линии, но к заряду Q2, так как этот заряд отрицателен.
 , (3)
, (3) .
.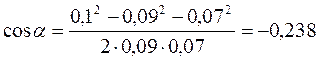
 (4)
(4) . (5)
. (5) .
. (6)
(6)


