
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод простой интерации явного типа решения некорректных задач с апостериорным выбором числа итерацийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При приближенном решении математических задач или прикладных задач весьма существенным является вопрос о том, корректна ли решаемая задача. Большинство некорректных задач может быть приведено к уравнению 1 рода, имеющему вид: в котором по заданному, не обязательно линейному оператору А, действующему из пространства X в пространство Y и по заданному элементу Определение. Задача определения решения x=R(y) из пространства Х по исходным данным Определение. Следуя Ж. Адамару, задачу отыскания Определение. Назовем задачу (1.1) корректной по Тихонову на множестве а) Точное решение задачи существует в классе М, б) принадлежащее множеству М решение задачи единственно для любой правой части у из множества Постановка задачи В действительном гильбертовом пространстве Н решается уравнение 1 рода Ах = у, (1) где А - ограниченный, положительный, самосопряжённый оператор, для которого нуль не является собственным значением. Причём нуль принадлежит спектру оператора А, т.е. задача некорректна. Предполагается существование единственного решения х при точной правой части у. Для его отыскания предлагается итеративный метод Однако на практике часто правая часть у уравнения (1) бывает неизвестной, а вместо у известно приближение
Если раскрыть скобки во втором слагаемом в (2) и (3), то Решение задачи Для решения Ax = y используется метод (3). Все результаты получены в предположении, что точное решение
Определим момент т останова итерационного процесса (3) условии
Предполагаем, что при начальном приближении Покажем, что правило останова по невязке применимо к методу (3). Рассмотрим семейство функций
Лемма 1. Пусть Лемма 2. Пусть Лемма 3. Пусть Используем доказанные леммы при доказательстве следующей теоремы. Теорема 1. Пусть Доказательство. По индукции легко показать, что Следовательно, Отсюда В силу лемм 1 и 2 имеем
Кроме того, из (5) и (6) следует, что Применим правило останова (4). Тогда Для Из (13) и (18) получаем при
Действительно, из (17) имеем Имеет место Теорема 2. Пусть выполнены условия теоремы 1 и пусть Доказательство. Имеем
(см. (17)). Тогда, поскольку соотношение (5) справедливо для любых n,то Замечание 1. Порядок оценки (19) есть
Замечание 2. Хотя формулировка теоремы 2 даётся с указаниями степени представимости s и истокопредставимого элемента z, на практике их значение не потребуется, так как они не содержатся в правиле останова (4). И тем не менее в теореме 2 утверждается, что будет автоматически выбрано количество итераций т, обеспечивающее оптимальный порядок погрешности. Но даже если истокопредставимость точного решения отсутствует, останов по невязке (4), как показывает теорема 1, обеспечивает сходимость метода, т.е. его регуляризующие свойства.
Понятие корректно поставленной и некорректно поставленной задачи. Пример. Неявный метод простой итерации решения некорректных задач с априорным выбором числа итераций. Пусть в гильбертовом пространстве Н требуется решить Опр. Задача определения решения Пример некорректной задачи: Х=У=L2(0,1). Интегральное уравнение Фредгольма 1-ого рода Опр. назовём задачу (1) корректной по Тихонову на множестве Будем решать ур-е (1) с помощью неявного итерационного метода:
Предполагая существование единственного точного решения x уравнения (1) при точной правой части у, ищем его приближение
Под сходимостью метода (3) понимается утверждение о том, что приближение Справедлива Теорема 1. Итерационный процесс (2) при условии Док-во: По индукции нетрудно показать, что
Разобьём полученный интеграл на 2 интеграла
При условии (4) величина
Покажем, что при тех же условиях процесс (3) можно сделать сходящимся, если нужным образом выбрать число итераций n в зависимости от уровня погрешности Теорема 2. При условии Доказательство: Будем считать
Тогда Теорема 3. Если точное решение ур-я (1) истокопредставимо, т.е. 58 .Метод обобщенного суммирования рядов для решения некорректных задач. При приближенном решении математических задач сущ. является вопрос корректно поставленной задачи. Задача наз. устойчивой - если бесконечно-малой вариации правой части уравнения, соответствует бесконечно-малые вариации левой части.
Задача наз. корректной по Адамару, если при любой фиксированной правой части правой части y=y0, точное решение: существует в x, единственно, устойчиво. Задача наз. корректной по Тихонову на мн-ве X, если: точное реш. сущ в M, ед при любом у из N, устойчиво. Метод обобщенного суммирования рядов предназначен для решения некорректных задач. Рассмотрим его на примере уравнения: zi(t) – соотв. полная, ортонормированная система собственных функций уравнения: Возьмем вместо точного y(t) – приближенное yδ(t) такое, что Рассмотрим: Оценить Найдем, при каком n эта оценка – оптимальна (принимает мин. значение).
Получим оптимальную оценку: Если имеет место s-кратная истокопредставимость, то
|
|||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.44.115 (0.007 с.) |

 (1.1)
(1.1) требуется определить решение х в пространстве Х.
требуется определить решение х в пространстве Х. можно указать такое число
можно указать такое число  , что неравенства
, что неравенства  следует, что
следует, что  где х 1= Ry 1, x2=Ry2, x1,x2
где х 1= Ry 1, x2=Ry2, x1,x2  X, y1,y2
X, y1,y2  из (1.1) называют корректной, если при любой фиксированной правой части у=у0 из Y ее решение: а) существует в пространстве Х; б) единственно в Х; в) устойчиво в Х. Если хотя бы одно из условий не выполняется, то задачу называют некорректной.
из (1.1) называют корректной, если при любой фиксированной правой части у=у0 из Y ее решение: а) существует в пространстве Х; б) единственно в Х; в) устойчиво в Х. Если хотя бы одно из условий не выполняется, то задачу называют некорректной. а само множество М – ее множеством корректности, если:
а само множество М – ее множеством корректности, если: , в) принадлежащие множеству М решение задачи устойчиво относительно любой правой части у из множества N.
, в) принадлежащие множеству М решение задачи устойчиво относительно любой правой части у из множества N. (2)
(2) , тогда метод (2) примет вид:
, тогда метод (2) примет вид: (3)
(3) исчезает, следовательно, вычислять
исчезает, следовательно, вычислять  и
и  не придётся.
не придётся. уравнения (1) истокопредставимо, т.е.
уравнения (1) истокопредставимо, т.е.  . Однако, поскольку сведения об элементе
. Однако, поскольку сведения об элементе  и степени истокопредставимости s имеются не всегда, то трудно определить число итераций п, обеспечивающих сходимость метода (3). Тем не менее этот метод можно сделать вполне эффективным, если воспользоваться следующим правилом останова по невязке.
и степени истокопредставимости s имеются не всегда, то трудно определить число итераций п, обеспечивающих сходимость метода (3). Тем не менее этот метод можно сделать вполне эффективным, если воспользоваться следующим правилом останова по невязке. (4)
(4) невязка достаточно велика, больше уровня останова ε, т.е.
невязка достаточно велика, больше уровня останова ε, т.е. 
 Нетрудно показать, что для
Нетрудно показать, что для  выполняются условия:
выполняются условия:  5)
5) 

 где
где  Справедлива
Справедлива . Тогда для
. Тогда для 
 . Тогда для
. Тогда для  имеет место соотношение
имеет место соотношение 
 и
и  при
при  имеем
имеем  то
то 
 в методе (3) выбирается по правилу (4). Тогда
в методе (3) выбирается по правилу (4). Тогда 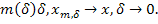







 и из (11) и (15) получим
и из (11) и (15) получим  . (17)
. (17)
 , поэтому
, поэтому  . Итак, для
. Итак, для 
 или
или (т.к. из (13)
(т.к. из (13)  ). Если при этом
). Если при этом  при
при  , то используя (10), получим
, то используя (10), получим  так как из (12)
так как из (12)  Если же для некоторых
Если же для некоторых  последовательность
последовательность  окажется ограниченной, то и в этом случае
окажется ограниченной, то и в этом случае 
 Следовательно,
Следовательно,  и по Лемме 3 получаем, что
и по Лемме 3 получаем, что  Отсюда
Отсюда  ч.т.д.
ч.т.д.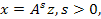 тогда справедливы оценки
тогда справедливы оценки 

 Воспользовавшись (18), получим
Воспользовавшись (18), получим  , откуда
, откуда  . При помощи неравенства моментов оценим
. При помощи неравенства моментов оценим 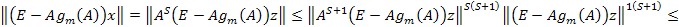

 ч.т.д.
ч.т.д. и он оптимален в классе задач с истокопредставимыми решениями
и он оптимален в классе задач с истокопредставимыми решениями 
 , где А – ограниченный, положительный и самосопряжённый оператор. Нуль не является собственным значением оператора, поэтому уравнение (1) имеет единственное решение. Предполагаем, что
, где А – ограниченный, положительный и самосопряжённый оператор. Нуль не является собственным значением оператора, поэтому уравнение (1) имеет единственное решение. Предполагаем, что  , поэтому задача (1) неустойчива и зн. некорректна.
, поэтому задача (1) неустойчива и зн. некорректна. из пространства Х по известной правой части
из пространства Х по известной правой части  наз. устойчивой на пространствах Х и У, если
наз. устойчивой на пространствах Х и У, если  Опр. Следуя Ж.Адамару, задачу отыскания
Опр. Следуя Ж.Адамару, задачу отыскания  из ур-я (1) наз. корректной (корректно поставленной), если при любой фиксированной правой части
из ур-я (1) наз. корректной (корректно поставленной), если при любой фиксированной правой части  из У её решение: 1) существует в пространстве Х; 2) единственно в Х; 3) устойчиво в Х. Если хотя бы одно условие не выполняется, то задачу наз. некорректной (некорректно поставленной).
из У её решение: 1) существует в пространстве Х; 2) единственно в Х; 3) устойчиво в Х. Если хотя бы одно условие не выполняется, то задачу наз. некорректной (некорректно поставленной). .
. , а само множество М - её множеством корректности, если: 1) точное решение задачи существует в классе М; 2) принадлежащее множеству М решение задачи единственно для любой правой части у из множества
, а само множество М - её множеством корректности, если: 1) точное решение задачи существует в классе М; 2) принадлежащее множеству М решение задачи единственно для любой правой части у из множества  ; 3) принадлежащее множеству М решение задачи устойчиво относительно любой правой части у из N. В случае нарушения любого из этих условий задачу (1) наз. некорректной.
; 3) принадлежащее множеству М решение задачи устойчиво относительно любой правой части у из N. В случае нарушения любого из этих условий задачу (1) наз. некорректной. (2)
(2) при приближённой правой части
при приближённой правой части  ,
,  . В этом случае метод примет вид
. В этом случае метод примет вид (3)
(3) подходит к точному решению х ур-я (1) при подходящем выборе n и достаточно малых
подходит к точному решению х ур-я (1) при подходящем выборе n и достаточно малых  , т.е.
, т.е.  .
. (4) сходится в исходной норме гильбертова пространства
(4) сходится в исходной норме гильбертова пространства  .
. . Используя интегральное представление самосопряжённого оператора
. Используя интегральное представление самосопряжённого оператора  спектральная ф-я,
спектральная ф-я,  . Так как уравнение (1) имеет по предположению единственное точное решение, то
. Так как уравнение (1) имеет по предположению единственное точное решение, то  и, следовательно,
и, следовательно, .
.
 , тогда
, тогда .
. Следовательно,
Следовательно,  , т.е. итеративный процесс (2) сходится, ч.т.д.
, т.е. итеративный процесс (2) сходится, ч.т.д. . Имеет место
. Имеет место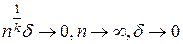 .
. и рассмотрим разность
и рассмотрим разность  . Как показано ранее,
. Как показано ранее,  . Воспользовавшись интегральным представлением самосопряженного оператора
. Воспользовавшись интегральным представлением самосопряженного оператора  , получим
, получим По индукции нетрудно показать, что
По индукции нетрудно показать, что  .
. . Поскольку
. Поскольку  и, как показано ранее,
и, как показано ранее,  , то при условии
, то при условии  .
.  .
. в пр-ве L2(0,1) c полным симметр. квадратично суммируемым ядром A(t,s). λ=0-принадлеж S(p), но не явл. его собственным значением. λi – собств. значения ядра, располож. в порядке убывания.
в пр-ве L2(0,1) c полным симметр. квадратично суммируемым ядром A(t,s). λ=0-принадлеж S(p), но не явл. его собственным значением. λi – собств. значения ядра, располож. в порядке убывания. где,
где,  . В этом случае решение запишется:
. В этом случае решение запишется: 
 , или, что то же самое, вместо точных коэф. Фурье – приближенные
, или, что то же самое, вместо точных коэф. Фурье – приближенные  ,
, 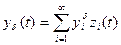 . Требуется по этим точным приближениям коэф. Фурье построить аппроксимацию для точного решения. В этом случае решение запишется:
. Требуется по этим точным приближениям коэф. Фурье построить аппроксимацию для точного решения. В этом случае решение запишется:  - т.к. задача не корректна, то этим рядом пользоваться нельзя. Не будем доводить суммирование этого ряда до конца, а воспользуемся некоторым конечным отрезком:
- т.к. задача не корректна, то этим рядом пользоваться нельзя. Не будем доводить суммирование этого ряда до конца, а воспользуемся некоторым конечным отрезком:  . Покажем, что это действительно можно сделать.
. Покажем, что это действительно можно сделать. . Первый член справа
. Первый член справа  ,
, 
 . Следов.: если n выбрать так, чтобы
. Следов.: если n выбрать так, чтобы  , то
, то  , при n=n(δ) →∞, для δ →0.
, при n=n(δ) →∞, для δ →0. невозможно без дополнит. предположения, т.к. неизв., и может быть сколь угодно малой скорость убывания нормы. Потребуем чтобы x было истокопредставимо:
невозможно без дополнит. предположения, т.к. неизв., и может быть сколь угодно малой скорость убывания нормы. Потребуем чтобы x было истокопредставимо:  . Из этого предположения следует, что сходится ряд x(t)=Az отсюда
. Из этого предположения следует, что сходится ряд x(t)=Az отсюда 
 и что
и что  . Оценим
. Оценим  , получим
, получим  .
. ,
,  отсюда
отсюда  ,
,  з.н. t*- min.
з.н. t*- min. при
при  .
.



