
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходимость метода итераций явного типа решения некорректных задач в энергетической норме.
В действительном гильбертовом пространстве
где
Однако на практике часто правая часть
Рассмотрим сходимость процессов (2) и (3) в энергетической норме Полагаем
Рассмотрим первое слагаемое Покажем по индукции, что При
Следовательно, формула (*) справедлива при Предполагаем, что формула (*) верна при
Покажем, что формула (*) справедлива для
Покажем, что Так как уравнение (1) имеет по определению единственное точное решение, то
Воспользовавшись интегральным представлением самосопряженного оператора, имеем:
где Известно, что Таким образом, при
для любых
и, следовательно,
Оценка для Оценим второе слагаемое в (4). Как было показано ранее, справедливо равенство
Воспользовавшись интегральным представлением самосопряженного оператора, получим
Обозначим через
Тогда получаем, Запишем общую оценку при условии (5):
Теорема 1. Итерационный процесс (3) при условии Оптимизируем полученную оценку (7) по
Получим, что оптимальная оценка погрешности не зависит от параметра Рассмотрим вопрос о том, когда из сходимости в энергетической норме следует сходимость в обычной норме гильбертова пространства Теорема 3. Если выполнены условия: 1) 2) то из сходимости Доказательство. Так как
Следовательно, Отсюда
Замечание 1. Так как Замечание 2. Использование энергетической нормы позволило получить оценки погрешности метода и априорный момент останова
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.232 (0.008 с.) |
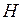 решается уравнение 1 рода
решается уравнение 1 рода (1)
(1)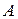 - ограниченный, положительный, самосопряженный оператор, для которого нуль не является собственным значением. Причем нуль принадлежит спектру оператора
- ограниченный, положительный, самосопряженный оператор, для которого нуль не является собственным значением. Причем нуль принадлежит спектру оператора  при точной правой части
при точной правой части 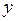 . Для его отыскания предлагается итеративный метод
. Для его отыскания предлагается итеративный метод (2)
(2)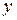 известно приближение
известно приближение 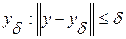 , тогда метод (2) примет вид:
, тогда метод (2) примет вид: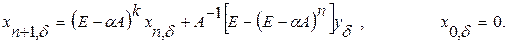 (3)
(3)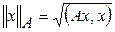 , где
, где 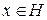 . При этом, как обычно, число итераций
. При этом, как обычно, число итераций 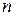 нужно выбирать в зависимости от уровня погрешности
нужно выбирать в зависимости от уровня погрешности  .
.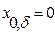 и рассмотрим разность
и рассмотрим разность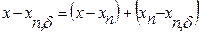 . (4)
. (4)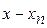 .
.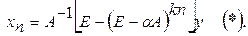
 из формулы (2) получаем:
из формулы (2) получаем: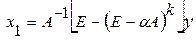 , т.к.
, т.к. 
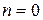 .
.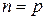 , т.е.
, т.е.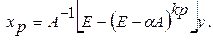
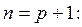
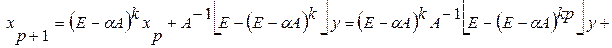


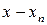 бесконечно мало в норме пространства
бесконечно мало в норме пространства  при
при 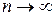 .
. и, следовательно,
и, следовательно,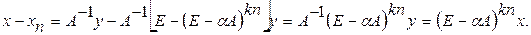
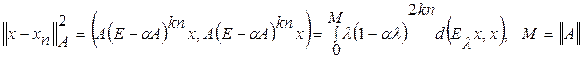 ,
,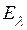 – соответствующая спектральная функция,
– соответствующая спектральная функция, 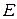 – единичный оператор. Для оценки нормы найдем максимум подынтегральной функции
– единичный оператор. Для оценки нормы найдем максимум подынтегральной функции 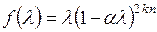 при
при 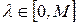 .
.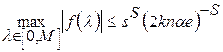 .
.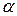 , удовлетворяющих условию
, удовлетворяющих условию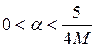 , (5)
, (5)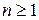 справедливо неравенство
справедливо неравенство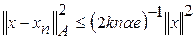 ,
, .
.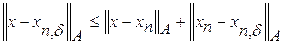 .
.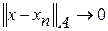 , при
, при 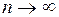 .
. .
.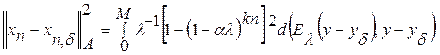 .
. подынтегральную функцию и оценим ее сверху при условии (5).
подынтегральную функцию и оценим ее сверху при условии (5).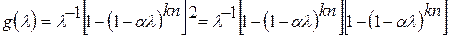 .
.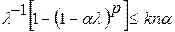 ,
, .
.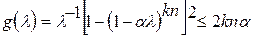 (6)
(6)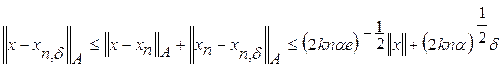 (7)
(7) сходится в энергетической норме гильбертова пространства
сходится в энергетической норме гильбертова пространства  из условия
из условия 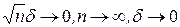 . Для процесса (3) справедлива оценка погрешности (7).
. Для процесса (3) справедлива оценка погрешности (7).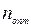 . Подставив
. Подставив 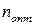 в оценку (7), получим ее оптимальное значение
в оценку (7), получим ее оптимальное значение 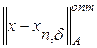 .
. . Поэтому для уменьшения
. Поэтому для уменьшения  ,
, , где
, где  ,
,  - фиксированное положительное число
- фиксированное положительное число  ,
, к
к 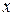 в энергетической норме следует сходимость в обычной норме гильбертова пространства.
в энергетической норме следует сходимость в обычной норме гильбертова пространства. и
и  и
и , т.е.
, т.е. .
. .
.



 , ч.т.д.
, ч.т.д. , то для того, чтобы
, то для того, чтобы  . Т.о. если
. Т.о. если  и
и  без требования знания истокопредставимости точного решения, что делает метод (3) эффективным и тогда, когда нет сведений об истокообразной представимости точного решения.
без требования знания истокопредставимости точного решения, что делает метод (3) эффективным и тогда, когда нет сведений об истокообразной представимости точного решения.


