Поиск и включение элемента в дерево.

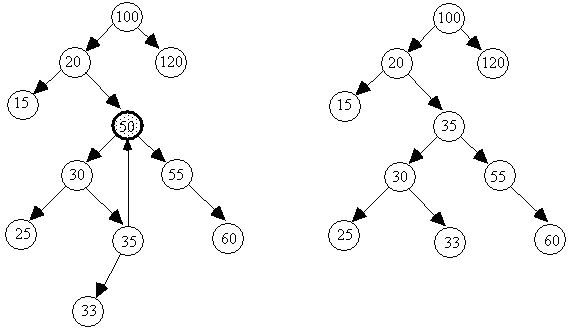
Задача. Задана последовательность слов. Определить частоту вхождения каждого из слов в последовательности.

Для решения задачи любое слово ищется в дереве, которое на начальном этапе пусто. Если слово найдено, то счетчик его вхождений увеличивается на 1, если нет, то слово включается в дерево с единичным значением счетчика.

Program Poisk;

Uses

Crt;

Type

Words = ^WordTree;

WordTree = record

Data: string;

k: integer;

Left, Right: Words;

end;

Var

n: integer;

kd: Words;

x: string;

f: text;

Procedure Tree(x: string; Var p: Words);

Begin

if p=nil

then

begin

new(p);

with p^ do

begin

k:= 1;

Data:= x;

Left:= Nil;

Right:= Nil;

end;

end;

else

if x>p^.Data

then

Tree(x. p^.Left)

else

if x<p^.Data

then

Tree(x. p^.Right)

else

Inc(p^.k);

End;

Procedure PrintTree(t: Words; h: integer);

Var

i: integer;

Begin

if t <> Nil

then

with t^ do

begin

PrintTree(Left, h+1);

for i:= 1 to h do

write(' ');

writeln(Data, ',(', k, ')');

PrintTree(Right, h+1);

end;

End;

Begin

ClrScr;

assign(f, 'c:\f.dan');

reset(f);

write('n=');

readln(n);

kd:= Nil;

while n>0 do

begin

readln(f,x);

Tree(x, kd);

Dec(n);

end;

close(f);

PrintTree(kd, 0);

readln;

End.

Эта задача называется задачей поиска по дереву с включением.

Задание. Наберите программу, протестируйте ее, вставьте комментарий, приготовьтесь объяснить учителю принцип поиска по дереву с включением. По желанию можете усложнить текст задачи, усовершенствовать ее решение или внести еще какие-либо изменения.

Удаление из дерева.

Непосредственное удаление элемента из упорядоченного дерева реализуется достаточно просто, если эта вершина является конечной или из нее выходит только одно ребро. Для этого нужно изменить соответствующую ссылку у предшествующей вершины.

Если же из удаляемой вершины выходит две ветви, то нужно найти подходящую вершину дерева, которую можно было бы вставить на место удаляемой вершины.

 

 

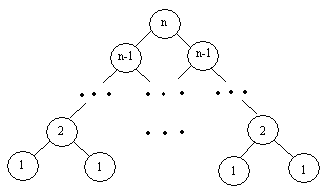
Из вышесказанного следует, что процедура удаления элемента из дерева должна различать три случая.

1. Удаляемая вершина имеет два поддерева. В этом случае удаляемый элемент нужно заменить либо на самый правый элемент его левого поддерева, либо на самый левый элемент его правого поддерева. При этом они должны иметь не больше одного потомка.

2. Удаляемая вершина имеет не более одного поддерева (0 или 1).

3. Удаляемой вершины в дереве нет.

Просмотрите рекурсивную процедуру DelTree, которая отыскивает элемент с заданным ключом и удаляет его. В процедуре DelTree описана процедура d1, которая работает только в первом из трех перечисленных случаев.

Вспомогательная процедура d1 "движется" по правой ветви левого поддерева исключаемого элемента q^ и заменяет значение ключа в q^ на соответствующее значение из самого правого элемента r^ левого поддерева.

Type

Pt = ^Node;

Node = Record

Data: integer;

Left, Right: Pt;

End;

Procedure DelTree(x: integer; Var p: Pt);

Var

q: Pt;

Procedure D1(Var r: Pt);

Begin

if r^.Right <> Nil

then

d1(r^.Right)

else

begin

q^.Data:= r^.Data;

q:= r;

r:= r^.Left;

Dispose(q);

end;

End;

Begin

if p=nil

then

writeln('Элемента с ключом ', x, 'в дереве нет.')

else

if x<p^.Data

then

DelTree(x, p^.Left)

else

if x>p^.Data

then

DelTree(x, p^.Right)

else

begin

q:= p;

if q^.Right = Nil

then

begin

p:= q^.Left;

dispose(q);

end;

else

if q^.Left = Nil

then

begin

p:= q^.Right;

dispose(q);

end;

else

D1(q^.Left)

end;

End;

Задание. Наберите программу, протестируйте ее, вставьте комментарий, приготовьтесь объяснить учителю принцип удаления элемента из дерева.

Выберите задачу для решения из предложенных ниже.

1. Удалите из дерева все равные между собой элементы. В программе используйте подпрограммы.

2. Удалите из дерева все повторяющиеся элементы. В программе используйте подпрограммы.

3. Постройте два дерева. Проверьте, является ли одно из них поддеревом другого. Если "да", то удалите это поддерево. В программе используйте подпрограммы.

4. Постройте два дерева. Проверьте, является ли одно из них поддеревом другого. Если "нет", то включите это поддерево. В программе используйте подпрограммы.

5. Используя очередь или стек, вычислите среднее арифметическое всех элементов непустого дерева Т и удалите все элементы меньшие этого числа. В программе используйте подпрограммы.

6. Используя очередь или стек, поменяйте местами максимальный и минимальный элементы непустого дерева Т, все элементы которого различны. В программе используйте подпрограммы.

7. Используя очередь или стек, напечатайте все элементы дерева Т по уровням: сначала – из корня дерева, затем (слева направо) – из вершин, дочерних по отношению к корню, затем (также слева направо) – из вершин, дочерних по отношению к этим вершинам, и т.д. В программе используйте подпрограммы.

8. Используя очередь или стек, найдите в непустом дереве Т длину (число ветвей) пути от корня до ближайшей вершины с элементом Е. Если такого элемента не обнаружено, то выдайте на экран соответствующее сообщение. В программе используйте подпрограммы.

9. Используя очередь или стек, подсчитайте число вершин на n-ом уровне непустого дерева Т (корень считайте вершиной 0-го уровня). В программе используйте подпрограммы.

10. Объедините два дерева в одно идеально сбалансированное. В программе используйте подпрограммы.

Задачи для самостоятельного решения (на усмотрение учителя)

1. Напишите программу, содержащую процедуру или функцию, которая присваивает параметру Е элемент из самого левого листа непустого дерева (лист – вершина, из которой не выходит ни одной ветви), используя очередь или стек. В программе используйте подпрограммы.

2. Напишите программу, содержащую процедуру или функцию, которая находит в непустом дереве длины (число ветвей) путей от корня до всех вершин, используя очередь или стек. В программе используйте подпрограммы.

3. Напишите программу, содержащую процедуру или функцию, которая подсчитывает число вершин на каждом уровне непустого дерева (корень считать вершиной 0-го уровня). В программе используйте подпрограммы.

4. Напишите программу, содержащую процедуру или функцию, которая определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от еорня дерева до листьев. В программе используйте подпрограммы.

5. Напишите программу, содержащую процедуру, которая строит Т1 – копию дерева Т. В программе используйте подпрограммы.

6. Напишите программу, содержащую процедуру Create(T,n), где n – положительное целое число, которая строит Т – дерево, изображенное на рисунке. В программе используйте подпрограммы.

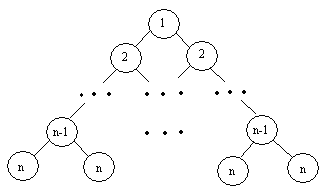
7. Напишите программу, содержащую процедуру Create(T,n), где n – положительное целое число, которая строит Т – дерево, изображенное на рисунке. В программе используйте подпрограммы.

8. Формулу вида

<формула>::=<терминал>|(<формула><знак><формула>)

<знак>::=+|-|*

<терминал>::=0|1|2|3|4|5|6|7|8|9

можно представить в виде двоичного дерева ("дерева-формулы") с элементами типа char согласно следующим правилам: формула из одного терминала (цифры) представляется деревом из одной вершины с этим терминалом, а формула вида (f1sf2) – деревом, в котором корень – это знак s, а левое и правое поддеревья – это соответствующие представления формул f1 и f2. Для примера посмотрите как будет выглядеть дерево, соответствующее формуле (5*(3+8)).

Опишите рекурсивную функцию или процедуру, которая:

а) вычисляет (как целое число) значение дерева-формулы Т);

б) по формуле из текстового файла f строит соответствующее дерево-формулу Т;

в) печатает дерево-формулу Т в виде соответствующей формулы;

г) проверяет, является ли двоичное дерево Т деревом-формулой.

9. Пусть в дереве-формуле (см. предыдущую задачу) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Опишите процедуру, которая:

а) упрощает дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f+0), (0+f), (f-0), (f*1), (1*f) на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f*0) и (0*f), на вершину с 0;

б) преобразует дерево-формулу Т, заменяя в нем все поддеревья соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3) и (f1*(f2+f3), f1*(f2-f3)) на поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3)) и ((f1*f2)+(f1*f3), (f1*f2)-(f1*f3)).

10. Во внешнем текстовом файле записана (без ошибок) некоторая программа на языке Паскаль. Известно, что в этой программе каждый идентификатор (служебное слово или имя) содержит не более 9 латинских букв и/или цифр. Напечатайте в алфавитном порядке все различные идентификаторы этой программы, указав для каждого из них число его вхождений в текст программы. Необходимо учесть, что в идентификаторах одноименные прописные и строчные буквы отождествляются, что внутри литерных значений, строк-констант и комментариев последовательности из букв и цифр не являются идентификаторами и что в записи вещественных чисел может встретиться буква Е или е.

 

Стеки. Очереди. Кольца

 

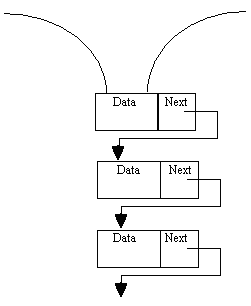
Занятие I

Тема. Стек. Отличия стека от списка. Основные операции со стеком.

На предыдущих занятиях мы уже рассматривали однонаправленный список. Здесь Вы познакомитесь с двумя разновидностями обычного линейного списка – стеком и очередью. В программировании наиболее часто используемой структурой является стек.

Стек – это линейный список, в котором добавление новых элементов и удаление существующих производится только с одного конца, называемого вершиной стека.

Стек часто называют структурой LIFO [сокращение LIFO означает Last In – First Out (последний пришел, первый вышел)]. Это сокращение представляет удобный способ запомнить механизм работы стека

Изобразим стек графически:

При программировании на Паскале стек реализуется чаще всего в виде однонаправленного списка. Каждый элемент структуры содержит указатель на следующий. Считается лишь, что для этого списка не существует обход элементов. Доступ возможен только к верхнему элементу структуры.

Стек предполагает вставку и удаление элементов, поэтому он является динамической, постоянно меняющейся структурой.

Стеки довольно часто встречаются в практической жизни. Простой пример: детская пирамидка. Процесс ее сборки и разборки подобен процессу функционирования стека.

Итак, если стек – это список, то добавление или извлечение элементов происходит с начала и только с начала (или возможно с конца и только с конца) списка.

Значением указателя, представляющего стек, является ссылка на вершину стека, каждый элемент стека содержит поле ссылки.

Таким образом, описать стек можно следующим образом:

Type

EXST = ^ST;

ST = record

Data: integer;

Next: EXST;

end;

Var

Stack: EXST; {Текущая переменная}

Если стек пуст, то значение указателя равно Nil.

Рассмотрим возможные операции со стеком.

Занесение элемента в стек

Занесение элемента в стек производится аналогично вставке нового элемента в начало списка. Процедура занесения элемента в стек должна содержать два параметра: первый задает вершину стека, в который нужно занести элемент, второй – заносимое значение элемента стека.

Процедура формирования стека будет иметь следующий вид:

Procedure FormStack;

Var

Stack: EXST; {Текущая переменная}

Digit: integer;

Procedure writeStack(Var u: EXST; Digit: integer);

Var

x: EXST;

Begin

new(x); {выделяем память под хранение нового элемента стека}

x^.Data:= Digit; {заполняем поле данных элемента}

x^.Next:= u; {новый элемент "связываем" со стеком}

u:= x; {созданный элемент определяем как вершину стека}

End;

Begin

Stack:= Nil; {инициализация стека}

writeln('Введите элементы стека. Окончание ввода – 0');

read(Digit);

while Digit <> 0 do

begin

writeStack(Stack, Digit);

read(Digit);

end;

End;