
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез в базисах И-НЕ, ИЛИ-НЕ.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее часто используются базисы, состоящие из одной функции: И-НЕ, ИЛИ-НЕ. Представление переключательной функции в этих базисах требует использования только этих операций с учетом ограничений по числу входов соответствующих элементов. Для этого используется закон Де Моргана: f(аbсd)=
Соответствующие схемы представлены на рис. 63.
Рис. 63. Реализация логической функции f(аbсd)= в базисе 2И-НЕ (а) и 2ИЛИ-НЕ (б), т.е. для двухвходовых элементов И-НЕ, ИЛИ-НЕ
В случае превышения ограничения по числу входов элементов следует еще раз применить закон Де Моргана, например:
т.е. получили только одноместные и двухместные операции И-НЕ. Синтез в базисе Жегалкина. Полиномом Жегалкина называется представление логической функции в базисе {Å,И,НЕ} (имеется соответствующая алгебра Жегалкина). В данном представлении инверсия реализуется как сумма по модулю 2 с константой 1. Для представления ДНФ в виде полинома Жегалкина необходимо выразить дизъюнкцию через конъюнкцию и инверсию. Например: хÚy= =xyÅxÅyÅ1Å1=xyÅxÅy. (1Å1=0). Пример. Представить в виде полинома Жегалкина логическую функцию xÚyÚz. xÚyÚz= =xyzÅxzÅyzÅxyÅxÅyÅ1Å1=xyzÅxzÅyzÅxyÅxÅy. Для преобразования полинома Жегалкина используются обычные приемы элементарной алгебры (исключение составляет равносильность аÅа=0). Полином Жегалкина может быть получен по таблице истинности путем суммирования по модулю 2 конъюнкций переменных без инверсии xi или инверсных переменных (xjÅ1) соответствующих рабочих наборов. Например, получим полином Жегалкина для функции f, таблица истинности которой имеет вид табл. 54. Таблица 54 Таблица истинности
Тогда получим: f=(xÅ1)(yÅ1)zÅ(xÅ1)y(zÅ1)Åx(yÅ1)(zÅ1)Åxyz= =(xyÅxÅyÅ1)zÅ(xzÅxÅzÅ1)yÅx(yzÅyÅzÅ1)Åxyz= =xÅyÅz, что и требовалось доказать, ибо и рассматривалась функция сложения по модулю 2 трех аргументов.
Булева производная
Производная первого порядка
где f(х1,х2,...,хi-1,1,xi+1,...,xn) – единичная остаточная функция, получаемая в результате подстановки вместо хi константы 1, а f(х1,х2,...,хi-1,0,xi+1,...,xn) – нулевая остаточная функция, получаемая в результате подстановки вместо xi константы 0. Пример. f=х1Úх2.
Пример.
Пример.
Булева производная по xi=0, если f не зависит от xi, булева производная по xi=1, если f зависит только от xi. Булева производная первого порядка определяет условия, при которых функция изменяет свое значение при изменении значения переменной xi В нашем примере функция f(х1х2х3) изменяет свое значение при изменении х1, если истинна конъюнкция х2х3, т.е. х2=1, х3=1. Пример. Определим все булевы производные функции
Итак, значение функции изменяется (функция переключается) при изменении х1, если х2=1 или х3=0 Смешанная булева производная k-го порядка определяется путем вычисления k раз булевых производных первого порядка от булевых производных первого порядка, например [9]:
Булева производная k-го порядка равна сумме по модулю 2 всех производных первых, вторых, третьих,..., k-х смешанных производных, и определяет условия, при которых функция изменяет значение при одновременном изменении соответствующих переменных, например:
Таким образом, f переключается при одновременном переключении х1, х2, когда х3=0, либо независимо от х3 при переключении х1 и х2 с 1,1 на 0,0 или с 0,0 на 1,1. При синтезе методом каскадов оптимальное исключение переменных достигается путем анализа веса производных [9]. Вес производной по данной переменной – число конституент соответствующей переключательной функции. То есть, сначала исключается переменная, производная которой имеет максимальный вес, что означает максимальное изменение функции при изменении переменной. 30 Элементарные автоматы памяти на основе комбинационного Автомата и задержки
Последовательностный автомат может быть синтезирован как композиция комбинационного автомата, реализующего функции переходов j и выходов y и элементарных автоматов памяти [10, 19], например, задержек на один такт (рис. 64).
Рис. 64. Задержка на один такт
Физически элементарный автомат памяти типа «задержка на один такт» реализуется линией задержки, которая может быть выполнена в виде специальных элементов – линий задержки или в виде соединения логических элементов, не инверсирующего сигнал, либо, в частных случаях, линией связи, поскольку передача сигнала по ней имеет некоторую конечную длительность, не превышающую длительность такта. Рассмотрим синтез элементарных автоматов памяти на основе задержек на один такт. Пусть требуется синтезировать автомат, выход которого устанавливается в состояние логической единицы при поступлении сигнала логической единицы на вход установки (обычно он обозначается S – «Set») и хранящий это состояние до поступления сигнала логической единицы на вход сброса (обычно он обозначается R – «Reset»). Таким образом, требуется создать автомат, имеющий два входа R и S и один выход, который обозначим z (рис. 65). Иногда добавляют и инверсный выход
Рис. 65. Элементарный автомат памяти Ясно, что синтезируется последовательностный автомат, так как его выходной сигнал зависит от последовательности поступления сигналов на входы:
Видно, что при одинаковых входных сигналах на входах SR, выходной сигнал может быть как 0, так и 1. В таком случае опишем функционирование автомата первичной таблицей переходов-выходов (табл. 55). Таблица 55 Первичная таблица переходов-выходов
Итак, в исходном состоянии автомат находится в строке с номером 1, в клетке, соответствующей нулевому состоянию RS. При поступлении набора сигналов 01 (начинается установка) автомат начинает переходить в состояние 2 (возникает неустойчивый такт 2), затем происходит перемещение во вторую строку – в устойчивый такт 2, обведенный кружком, при этом на выходе возникает сигнал 1. При поступлении сигнала 10 в первой строке и сигналов 00, 01 во второй строке состояние автомата не меняется, состояние 11 считается невозможным. Очевидно, что сокращение числа строк табл. 55 невозможно, иначе мы имели бы комбинационный автомат (у которого одно состояние – одна строка). Приступим к кодированию состояний. Оно в данном случае тривиально: исходное состояние сопоставим с состоянием 0 (1 строка), другое состояние сопоставим с 1. Получим таблицы переходов-выходов для автомата Мили (табл. 56) и автомата Мура (табл. 57). Таблица 56 Таблица переходов-выходов элементарного автомата памяти Мили
Таблица 57 Таблица переходов-выходов элементарного автомата памяти Мура
Таким образом, для автомата Мура (табл. 57) z(t)=y(t). Построим автомат Мура. Получим функции переходов y(t+1) и выходов z(t):
Минимизируя y(t+1) по карте Карно, какой и является табл. 57, получаем:
Реализуем эту функцию в виде переключательной схемы (рис. 66).
Рис. 66. Переключательные схемы элементарного автомата памяти Мура
На рис. 66 Y – хранитель состояния автомата (например, обмотка реле), обратная связь, указанная пунктиром реализует так называемую самоблокировку. Задержка на один такт осуществляется следующим образом: сначала срабатывает Y, затем замыкается его контакт y. Технически предполагается, что к моменту размыкания S, y уже замкнут. Построим схему на функциональных элементах в базисе И-НЕ:
Таким образом, один элемент 2И-НЕ реализует функцию Соответствующая схема показана на рис. 67.
Рис. 67. Реализация элементарного автомата памяти на функциональных элементах 2И-НЕ
Можно заметить, что выход второго элемента в цепи R при R=0 соответствует значению
Рис. 68. Элементарный автомат памяти RS триггер
Это известная схема так называемого RS триггера. Его условное графическое обозначение приведено на рис. 69.
Рис. 69. Условное графическое обозначение RS триггера
Для описания работы элементарных автоматов памяти применяются таблицы возбуждения, указывающие условия перехода от текущего к последующему внутреннему состоянию. Такая таблица для RS триггера – табл. 58. Таблица 58 Таблица возбуждения RS триггера
Аналогично выглядит таблица и для такого элементарного автомата памяти как дистанционный переключатель, который имеет механическую обратную связь (механическую фиксацию состояния) и широко применяется в автоматике – рис. 70.
Рис. 70. Условное графическое обозначение дистанционного переключателя
Задержка на один такт может быть реализована и так называемым D триггером, устанавливающимся в состояние, определяемое его входом D по специальному разрешающему сигналу – синхроимпульсу. Это уже синхронный автомат в отличие от рассмотренных выше асинхронных (рис. 71, табл. 59).
Рис. 71. Условное графическое обозначение синхронного D триггера
Косая черта с наклоном вперед на входе синхронизации обозначает срабатывание по фронту синхроимпульса. Таблица 59 Таблица возбуждения D триггера
D триггер без синхронизации – аналог обычного реле (рис. 72).
Рис. 72. Условное графическое обозначение реле и временная диаграмма работы
Имеются и другие элементарные автоматы памяти, например, асинхронный RS триггер с инверсным управлением (нулями, а не единицами, рис. 73, табл. 60), синхронный JK триггер (рис. 74, табл. 61).
Рис. 73. Условное графическое обозначение RS триггера с инверсным управлением
Таблица 60 Таблица возбуждения RS триггера с инверсным управлением
Рис. 74. Условное графическое обозначение синхронного JK триггера,
срабатывающего по заднему фронту импульса
Таблица 61 Таблица возбуждения синхронного JK триггера, срабатывающего по заднему фронту импульса
При синтезе сложных последовательностных автоматов на основе элементарных автоматов памяти (элементов памяти) для получения функций, описывающих управление ими комбинационной частью автомата, строится таблица возбуждения элементарных автоматов памяти (таблица возбуждения элементов памяти).
31 Синтез автомата – распознавателя последовательности Дано: кодовая последовательность 0-1-3-2 двоичного двухразрядного сигнала (в десятичном коде). Получить ПФ, описывающие соответствующий конечный автомат-распознаватель последовательности (рис. 75).
Рис. 75. Распознаватель последовательности на входах а, b
Последовательность поступает на входы a,b конечного автомата (КА):
Это правильная последовательность изменения входов a,b в соответствии с заданием. Возможны и неправильные последовательности из алфавита А={0,1,2,3}. Ограничим возможные неправильные коды изменением только одного двоичного разряда. Рассмотрим соответствующий квадрат соседних чисел (рис. 76, т.к. всего два входа).
Рис. 76. Иллюстрация изменения входов
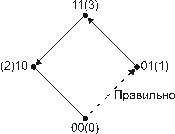
Направление изменения входных кодов показано стрелками. Видно, что в начале из 00 (0) имеем переход в 01 (1). Это если последовательность правильная. А если не правильная? Тогда возможен лишь один вариант (рис. 77).
Рис. 77. Иллюстрация возможного нарушения последовательности: из 00(0) в 10(2)
На втором шаге правильно: 01 (1) в 11 (3), а неправильно (рис. 78)?
Рис. 78. Иллюстрация возможного нарушения последовательности: из 01(1) в 00(0)
Т.е. возможен возврат, в 00. Аналогично на третьем шаге неправильным будет переход (рис. 79) из 11 (3) в 01 (1).
Рис. 79. Иллюстрация возможного нарушения последовательности: из 11(3) в 01(1)
Таким образом, можно построить граф возможных последовательностей (рис. 80).
Рис. 80. Граф последовательностей распознавателя 0-1-3-2
Таким образом, имеем всего 4 последовательности: 1) 0-1-3-2 (правильная); 2) 0-2 (неправильная); 3) 0-1-0 (неправильная); 4) 0-1-3-1 (неправильная). Строим первичную таблицу переходов (ПТП) соответствующего конечного автомата – распознавателя последовательности 0-1-3-2 (табл. 62).
Таблица 62 Первичная таблица переходов-выходов распознавателя 0-1-3-2
Здесь (см. табл. 62) кружком обведены устойчивые такты работы автомата-распознавателя. Переход от одного устойчивого такта в соответствующей строке таблицы переходов-выходов к другому осуществляется через неустойчивый такт. В каждой строке ПТП только один устойчивый такт, номер которого соответствует номеру строки. Можно получить переключательные функции и по ПТП, но в большинстве случаев пытаются сократить число строк первичной таблицы переходов («сжать» ПТП), т.е получить минимизированную таблицу переходов (МТП).
Это удобно делать путем построения графа объединения строк. В таком графе число вершин равно числу строк ПТП. В нашем случае – 7. Ребром соединяются вершины, соответствующие двум строкам, которые можно слить в одну строку, т.е. в этих строках клетки не противоречат друг другу. Такими клетками будут: 1) пустые клетки и клетки с цифрами, и наоборот; 2) клетки с цифрой i и клетки с цифрой в кружке, и наоборот, т.е. соответствующие неустойчивый и устойчивый такты сливаются в один устойчивый такт. Граф объединения строк показан на 81.
Рис. 81. Граф объединения строк
Теперь в графе объединения строк необходимо выделить минимальное количество максимальных полных подграфов. В нашем случае это подграфы 3,4,6,7; 1,5 и одна вершина 2. Возможны другие варианты объединения. Но ни при одном варианте мы не получим две строки (это идеал – к нему надо стремиться). Получим минимизированную таблицу переходов (табл. 63). Таблица 63 Минимизированная таблица переходов
Приступим к кодированию состояний автомата. Применим соседнее кодирование, которое характеризуется тем, что строки МТП, между которыми имеются переходы, должны быть закодированы соседним кодом (кодом, отличающимся только в одном разряде). Это необходимо для повышения надежности автомата, чтобы не было неоднозначности переходов из состояния в состояние. Кодирование может иметь вид:
I: 00 II: 01 III: 11
Т.е. необходимо два двоичных разряда, которые обозначим y1y2. Это не что иное, как текущее состояние автомата, которое принято обозначать у2(t) y1(t) или сокращенно у2 y1(t). Теперь получим таблицу переходов-выходов (ТПВ, табл. 64), в которой указывается, как автомат переходит из текущего состояния (коды строки) в последующее (у2y1(t+1) – код в некоторой клетке) при различных комбинациях входов ab. Таблица 64 Таблица переходов-выходов
Код клетки – это соединение (конкатенация) двоичного кода строки и столбца, представленные в виде десятичного числа. Очевидно, что кружки в МТП и ТПВ располагаются в одинаковых клетках. Если такт устойчивый, то в кружке ТПВ в числителе указывается номер соответствующей строки. Если такт неустойчивый – то указывается код той строки, в которую осуществляется переход. В знаменателе указываются выходные сигналы z2z1. Они берутся из первичной таблицы переходов-выходов. Так, если в клетке МТП находится цифра 5 (пятый такт), то из пятой строки ПТП берется код 10 (нарушение последовательности). Указываем это число в клетке 2 ТПВ ( Теперь получаем все четыре ПФ, описывающие наш автомат в символической форме:
По этим ПФ можно построить схему автомата, предварительно проведя минимизацию. Получим структурную схему автомата (рис. 82).
Рис. 82. Структурная схема автомата-распознавателя
34 Представление чисел в ЭВМ в двоично-кодированном десятичном формате (BCD или десятичном). В BCD-формате десятичные цифры хранятся в виде 4-битных двоичных эквивалентов. В упакованном BCD-формате цепочка десятичных цифр хранится в виде последовательности 4-битных групп, например: 9502 в виде 1001 0101 0000 0010. В неупакованном BCD-формате каждая цифра хранится в младшей тетраде соответствующего байта.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 2241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.47.172 (0.013 с.) |

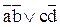 =
=  =
=  – это представление в базисе И-НЕ.
– это представление в базисе И-НЕ. – это представление в базисе ИЛИ-НЕ.
– это представление в базисе ИЛИ-НЕ.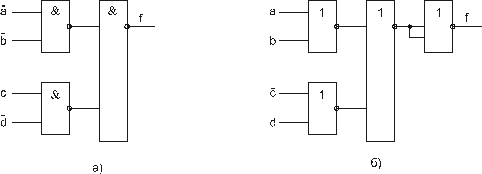
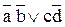

 =(хÅ1)(yÅ1)Å1=
=(хÅ1)(yÅ1)Å1= =(хÅ1)(yÅ1)(zÅ1)Å1=(xyÅxÅyÅ1)(zÅ1)Å1=
=(хÅ1)(yÅ1)(zÅ1)Å1=(xyÅxÅyÅ1)(zÅ1)Å1=
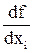 от булевой функции f по переменной xi определяется следующим образом [9]:
от булевой функции f по переменной xi определяется следующим образом [9]:







 .
.



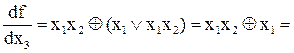

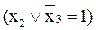 ; при изменении х2, если х1=х3=1 (х1х3=1); при изменении х3, если х1=1; х2=0
; при изменении х2, если х1=х3=1 (х1х3=1); при изменении х3, если х1=1; х2=0  .
.





 .
.
 ,
,



 .
.

 , второй –
, второй –  .
.
 . Эту схему часто изображают в несколько другом виде, полагая, что задержка реализуется в линии связи (рис. 68).
. Эту схему часто изображают в несколько другом виде, полагая, что задержка реализуется в линии связи (рис. 68).















 ).
).




