
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о переключательных схемах и технической реализации переключательных функцийСодержание книги
Поиск на нашем сайте
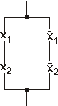
Исторически первое практическое применение теория переключательных функций нашла в так называемых переключательных схемах (ПС, контактных схемах). Такие схемы построены на механических переключателях и реле (дистанционных переключателях), содержащих контакты двух типов: замыкающие, обозначаемые: и размыкающие, обозначаемые: При этом параллельное соединение контактов соответствует дизъюнкции, а последовательное – конъюнкции. Например, переключательная схема, реализующая импликацию х1®х2 имеет вид рис. 29. Такая схема приводит ток, если х2 замкнут (сработал), или х1 замкнут (не сработал).
Рис. 29. Переключательная схема, реализующая импликацию х1®х2
Переключательная реализация функции
Рис. 30. Переключательная реализация
Предполагается, что контакты срабатывают, когда подается напряжение на обмотки соответствующих реле, не изображенных на рис. 29-30 или нажимаются соответствующие кнопки, включаются соответствующие тумблеры и т.д. Иногда с целью упрощения переключательные схемы изображают в виде только символов контактов (рис. 31).
Рис. 31. Упрощенная переключательная схема эквиваленции х1«х2
Таким образом, каждой такой последовательно-параллельной схеме можно поставить в соответствие некоторую логическую функцию (формулу логики). Переключательная схема – схема из замыкающих, размыкающих и переключающих контактов показана на рис. 32.
Рис. 32. Переключательная схема
Последовательно-параллельная контактная схема соответствует конкретной ПФ. Упрощенная ПС изображается в символах переменных (рис. 33).
Рис. 33. Упрощенная переключательная схема
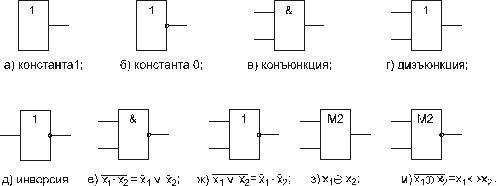
Применяя равносильные преобразования ПФ, которые рассматриваются далее, можно упрощать ПС, уменьшая число контактов. Возможна реализация ПФ схемами из функциональных элементов, программно. Техническая реализация базисных логических функций может быть основана на использовании различных физических явлений, например, базисы И-НЕ, ИЛИ-НЕ – явлений в полупроводниках, импликация – магнитных явлений. В ряде случаев используются пневматическая реализация (струйные элементы), гидравлическая реализация, оптическая реализация. Переключательные (логические) элементы изображают в виде прямоугольников, в которых инверсные входы и выходы изображают в виде кружков, а символы логических операций указывают в верхней части прямоугольника. Это условное графическое обозначение логических элементов (рис. 34).
Рис. 34. Условное графическое обозначение логических элементов по стандарту РФ Путем соединения логических элементов получают схему, реализующую требуемую логическую функцию в виде суперпозиции базисных функций, каждая из которых реализуется определенным логическим элементом. В электронных приборах конъюнкция и дизъюнкция реализуются соответственно последовательным и параллельным соединением ключевых полупроводниковых элементов, отрицание – включением нагрузки в коллекторную цепь транзистора [9]. Так, переключательная функция
Рис. 35. Реализация ПФ транзисторной схемой
Здесь кружки – это транзисторы, то есть элементарные бесконтактные переключатели (ключи), прямоугольники – это резисторы. На один из полюсов схемы подается напряжение питания, на другой «ноль вольт». Реализация импликации может быть основана на использовании магнитных процессов. Представление функции
Переключательные схемы и схемы из функциональных элементов реализуют так называемые конечные автоматы, о которых речь будет идти в дальнейшем. 19 Основные законы булевой алгебры переключательных функций Формулы ПФ f1 и f2 равносильны, если их эквиваленция f1«f2 является тождественно истинной (тавтологией). Равносильность, как правило, обозначается º, но мы будем «нестрого» использовать в дальнейшем и простое равенство =. Равносильность – это некоторое отношение, которое обладает следующими свойствами: а) оно рефлексивно, т.е. fºf, всякая формула f равносильна самой себе; б) оно симметрично: если f1ºf2, то f2ºf1; в) оно транзитивно: если f1ºf2 и f2ºf3, то f1ºf3. Равносильности формул алгебры логики часто называют законами. Они подобны законам алгебры множеств. Говорят, что булева алгебра логических (переключательных) функций изоморфна булевой алгебре множеств. Законы булевой алгебры: 1) хºх – закон тождества. Закон тождества означает, что мысль, заключенная в некотором высказывании, соответствующем двоичной переключательной функции остается (считается) неизменной на протяжении всего рассуждения. 2) 3) 4) 5) х×хºх; хÚхºх – закон идемпотентности (от латинского idem – то же, potentio – сила). Этот закон рассматривается относительно операций конъюнкции и дизъюнкции. В силу закона идемпотентности в алгебре логики, как и в алгебре множеств, нет показателей степеней, коэффициентов. Оказывается, основные законы алгебры логики двойственны (справедливы относительно конъюнкции и дизъюнкции). 6) х×yºy×х; xÚyºyÚх – закон коммутативности (переместительности). 7) х×(y×z)º(x×y)×z; xÚ(yÚz)º(xÚy)Úz – закон ассоциативности (сочетательности). 8) х×(yÚz)ºxyÚхz; xÚyz)º(xÚy)Ú(хÚz) – закон дистрибутивности (распределительности). Закон дистрибутивности относительно дизъюнкции не имеет аналога в обычной алгебре. 9) 10) xÚхyºх; х(xÚy)ºх – закон поглощения. Короткий член конъюнкции (дизъюнкции) поглощает длинный член, содержащий короткий в качестве составной части. 11) 12) Еще раз отметим двойственность законов алгебры логики: они действуют как относительно дизъюнкции, так и относительно конъюнкции. Кроме перечисленных законов, которые можно доказать, например, построив соответствующие таблицы истинности (соответствия), большое значение имеют так называемые соотношения 0 и 1, полученные на основании законов алгебры логики:
причем 1Ú0=1; 1×0=0; 0Ú1=1; 0×1=0. Здесь мы стали применять простое равенство (=). Рассмотренные законы применимы не только к отдельным переменным, но и к группам переменных, объединенных операциями алгебры логики, т.е. х, например, может быть в свою очередь конъюнкцией В алгебре переключательных функций установлен порядок выполнения действий. При отсутствии в выражении скобок первыми выполняются операции отрицания (инверсии), затем операции конъюнкции и последними – дизъюнкции. При наличии в выражении скобок в первую очередь выполняются операции внутри скобок.
Равносильные преобразования.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.213 (0.007 с.) |

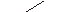 .
.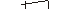 .
.
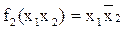 имеет вид рис. 30.
имеет вид рис. 30.
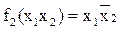
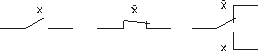

 реализуется, как показано на рис. 35.
реализуется, как показано на рис. 35.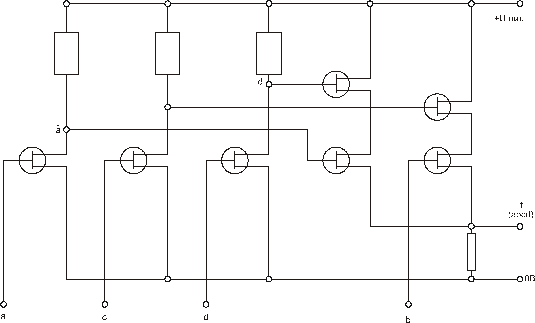
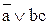 в виде суперпозиции операций ® выглядит следующим образом:
в виде суперпозиции операций ® выглядит следующим образом: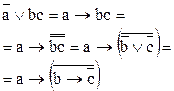
 – закон противоречия. Закон противоречия гласит, что никакое предложение не может быть истинным одновременно со своим отрицанием.
– закон противоречия. Закон противоречия гласит, что никакое предложение не может быть истинным одновременно со своим отрицанием.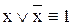 – закон исключенного третьего. Закон исключенного третьего говорит о том, что для каждого высказывания имеется лишь две возможности: быть либо истинным, либо ложным. Третьего не дано.
– закон исключенного третьего. Закон исключенного третьего говорит о том, что для каждого высказывания имеется лишь две возможности: быть либо истинным, либо ложным. Третьего не дано. – закон двойного отрицания.
– закон двойного отрицания. ;
;  закон Де Моргана. Отрицание конъюнкции высказываний равносильно дизъюнкции отрицаний этих высказываний. Отрицание дизъюнкции высказываний равносильно конъюнкции отрицаний этих высказываний.
закон Де Моргана. Отрицание конъюнкции высказываний равносильно дизъюнкции отрицаний этих высказываний. Отрицание дизъюнкции высказываний равносильно конъюнкции отрицаний этих высказываний.
 – закон склеивания. Здесь склеивание производится по переменной y; она исключается, если входит в члены дизъюнкции (конъюнкции) с разными знаками, а остальные элементы в конъюнкции (дизъюнкции) с ней одинаковы.
– закон склеивания. Здесь склеивание производится по переменной y; она исключается, если входит в члены дизъюнкции (конъюнкции) с разными знаками, а остальные элементы в конъюнкции (дизъюнкции) с ней одинаковы.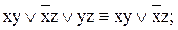
 – закон обобщенного склеивания, т.е. в дизъюнкции конъюнкций «лишней» является конъюнкция, полученная в результате конъюнкции членов перед инверсной и неинверсной переменной в двух других конъюнкциях. То же можно сказать и о конъюнкции дизъюнкций, в которых имеются дизъюнкции с такими переменными.
– закон обобщенного склеивания, т.е. в дизъюнкции конъюнкций «лишней» является конъюнкция, полученная в результате конъюнкции членов перед инверсной и неинверсной переменной в двух других конъюнкциях. То же можно сказать и о конъюнкции дизъюнкций, в которых имеются дизъюнкции с такими переменными.
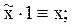

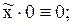
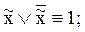
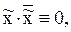
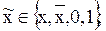 два последних соотношения – это закон исключенного третьего и закон противоречия. Так, например:
два последних соотношения – это закон исключенного третьего и закон противоречия. Так, например: а
а  .
.


