Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упрощение формул алгебры переключательных функцийСодержание книги Поиск на нашем сайте
Равносильные преобразования – это замена одной формулы другой, равносильной формулой. Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными. Под упрощением формулы будем понимать равносильные преобразования, приводящие к формуле, содержащей меньшее число переменных, чем исходная. Такие преобразования формул логики необходимы при синтезе, анализе, контроле дискретных устройств, а в последнее время – в системах искусственного интеллекта (логического вывода). Мощным аппаратом для таких равносильных преобразований помимо рассмотренных законов алгебры логики являются так называемые основные формулы равносильных преобразований, полученные с использованием этих законов [34]. Пусть Пусть
Такая запись означает, что:
Условно замену переменных на константу в функции f обозначаем стрелками. Примеры.
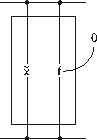
Для облегчения запоминания рекомендуется мнемоническое правило [34]. Представим формулу равносильного преобразования относительно конъюнкции из вида переключательной схемы, в которой конъюнкции
Рис. 39. Иллюстрация мнемонического правила для формулы равносильных преобразований относительно конъюнкции
Рассмотрим формулу равносильных преобразований относительно дизъюнкции. Если переменная
Это означает, что:
Примеры.
f(аbс)= В этой функции в явном виде нет отдельной переменной (
Отсюда:
Имеется соответствующее мнемоническое правило. Представим формулу равносильного преобразования относительно дизъюнкции в виде переключательной схемы, в которой дизъюнкции
Рис. 40. Иллюстрация мнемонического правила для формулы равносильных преобразований относительно дизъюнкции
Основные формулы равносильных преобразований можно доказать методом подстановки в них вместо переменной х ее возможных значений 0, 1 и сравнения правой и левой частей уравнения. Докажем, например, формулу:
Пусть х=0; тогда левая часть формулы:
а правая:
т.е. равенство справедливо. Пусть х=1; тогда левая часть формулы
а правая часть формулы
Равенство также справедливо, несмотря на отличия в функции f. Аналогично доказывается формула для конъюнкции, например:
При х=0:
равенство справедливо, несмотря на отличия в функции f. При х=1:
равенство также справедливо. Основные формулы равносильных преобразований имеют следствия, которые позволяют разложить логическую функцию по любой переменной. Следствие 1.
Следствие может быть доказано путем конъюнкции функции с тождественно истинной формулой
Это известное разложение Шеннона. Пример 1. Разложить логическую функцию по переменной b: f(аbсd)=а =b{а×0Ú(
Следствие 2.
Доказательство: f=fÚ0=fÚх×
Пример 2. Разложим ту же функцию f(авсd) (пример 1) по переменной а с помощью следствия 2: f(аbсd)={аÚ0×
20 Преобразование форм представления переключательных функций Одним из способов задания переключательных функций является их представление в виде аналитических выражений (формул). Существуют дизъюнктивная, конъюнктивная и смешанная (скобочная) формы. Рассмотрим дизъюнктивные формы представления переключательных функций. Выражение вида Если логическая функция, зависящая от n переменных, записана в виде дизъюнкции элементарных конъюнкций ЭК1ÚЭК2Ú...ÚЭКr и хотя бы одна ЭК не содержит все n переменных, то такая форма задания называется дизъюнктивной нормальной формой (ДНФ). ДНФ – дизъюнкция конечного множества попарно различных элементарных конъюнкций. Например: f(аbсd)=аÚ Произвольная функция, например, так называемая скобочная форма, может быть приведена к ДНФ следующим образом: · выполнить все операции инверсии, применяемые к логическим выражениям (группе переменных); · раскрыть все скобки; · в полученном выражении произвести все упрощения. Например: f(х1х2х3)= = = Получили ДНФ функции f(х1х2х3). Если все элементарные конъюнкции, входящие в ДНФ, содержат все n переменных, от которых зависит функция, то такая форма называется совершенной дизъюнктивной нормальной формой (СДНФ). СДНФ может быть получена по рабочим (единичным) наборам функций, например по таблице истинности, и наоборот, если задана СДНФ, можно получить таблицу истинности. Однако, если не оговорены условные наборы, все остальные наборы, кроме наборов, соответствующих членам СДНФ, будут считаться запрещенными. Пусть задана таблица истинности функции сложения по модулю 2 (Å) (табл. 32). Таблица 32 Таблица истинности
Тогда z(аb)= Первый член СДНФ соответствует строке 01, второй – строке 10. Элементарные конъюнкции, входящие в СДНФ функции, называются конституентами единицы (или минтермами). Конституента единицы обращается в 1 (истинна) на единственном наборе значений переменных. Так, подстановка входного набора 01 (база аb) обращает в 1 конституенту От СДНФ легко перейти к номерам рабочих наборов в различных системах. Так: z(аb)®012Ú102®110Ú210. Аналогично по СДНФ можно получить рабочие наборы, считая остальные запрещенными: z(аb)=1,2[0,3]. Получили символическую форму задания логической функции в десятичных номерах рабочих и запрещенных наборов. Очевидно, не составляет труда и обратный переход – от символической формы, от номеров наборов – к СДНФ. Для преобразования ДНФ в СДНФ можно выполнить конъюнкцию каждой элементарной конъюнкции, не содержащую i-ю переменную, с тождественно истинным выражением Пример.
Получили СДНФ.
Имеется способ получения СДНФ из ДНФ с использованием обобщенного кода, в котором для обозначения недостающих переменных в соответствующих позициях используются знаки «–» (или «~» – «тильда»), а для остальных – символы 0,1. Пример. Функцию Тогда, подставляя вместо «–» всевозможные комбинации 0,1, получим:
Таким образом, получили номера 000, 001, 011, которые соответствуют членам СДНФ. СДНФ переключательной функции, тождественно равной 1 (тождественно истинной), содержит 2n констинтуэнт (n – число переменных). Переключательная функция может быть представлена в конъюнктивной форме. Выражение вида Если переключательная функция, зависящая от n переменных, записана в виде конъюнкции элементарных дизъюнкций ЭД1·ЭД2·...·ЭДr и хотя бы одна ЭД не содержит все n переменных, то такая форма задания называется конъюнктивной нормальной формой (КНФ). КНФ – конъюнкция конечного множества попарно различных элементарных дизъюнкций. Например: f(аbсd)=а( Произвольная функция, например, скобочная форма, может быть всегда приведена к КНФ следующим образом: · заданную функцию инверсировать, получить ДНФ инверсной функции; · ДНФ инверсной функции инверсировать еще раз, получить тождественную исходной функцию в КНФ; · на каждом этапе следует производить необходимые упрощения. Пример. f(х1х2х3)=
=
Получили КНФ. Второй способ получения КНФ заключается в выполнении всех операций инверсии, применяемой к группе переменных (логическим выраженииям), затем используется распределительных закон. Пример. f(х1х2х3)= = =
Если все элементарные дизъюнкции, входящие в КНФ, содержат все n переменных, от которых зависит функция, то такая форма называется совершенной конъюнктивной нормальной (СКНФ). СКНФ может быть получена по запрещенным (нулевым) наборам функции, например по таблице истинности. Для получения СКНФ по таблице истинности необходимо составить элементарные дизъюнкции всех переменных для каждой строки таблицы, в которой функция равна 0. При этом в дизъюнкцию входит сама переменная, если ее значение равно 0, и отрицание переменной, если ее значение равно 1. Так, для функции сложения по модулю 2 (табл. 32) СКНФ имеет вид:
Элементарные дизъюнкции, входящие в СКНФ функции, называются конституентами нуля (макстермами). Конституента нуля обращается в нуль на единственном наборе переменных, который является запрещенным (нулевым) набором функции. Например, для функции сложения по модулю 2 конституента нуля (аÚb) обращается в 0 на наборе 00, а конституента нуля
От СКНФ можно перейти к номерам запрещенных наборов в различных системах счисления. Для получения двоичных номеров в порядке базы функции (например, аb) необходимо заменить символы переменных с инверсией на 1, а без инверсии – на 0 и записать вместо элементарных дизъюнкций соответствующие совокупности двоичных чисел. Если дополнительной информации нет, то все остальные числа из области задания функции считаются рабочими. Для преобразования КНФ в СКНФ можно выполнить дизъюнкцию каждой элементарной дизъюнкции, не содержащей i-ю переменную, с тождественно ложным выражением Например:
Соответствующие запрещенные наборы: 100, 110, 101, 111, 010 (база х1х2х3). Получим СДНФ и СКНФ ПФ, заданной десятичным номером №17410. Таблица истинности ПФ №17410 показана в табл. 33 Таблица 33 Таблица истинности
СДНФ – совершенная дизъюнктивная нормальная форма:
СКНФ – совершенная конъюнктивная нормальная форма:
21 Цель минимизации переключательных функций
При технической реализации переключательных функций, широко используемых в вычислительной технике, системах автоматического (автоматизированного) управления и контроля, возникает задача нахождения наиболее экономичного представления соответствующих переключательных функций. По существу решается задача оптимизации, причем минимизируется стоимость реализации. Понятие стоимости устройства, реализующего переключательную функцию – дискретного устройства – относительно. Для переключательных схем, реализуемых в виде релейно-контактных схем, для схем из корпусных транзисторов и резисторов, из микросхем логических элементов малой степени интеграции, минимизация числа реле, контактов, транзисторов, числа микросхем и означает снижение стоимости [28]. Это было особенно актуально на ранних этапах развития дискретной, цифровой техники. Для современных цифровых автоматов на больших и сверхбольших интегральных схемах (БИС и СБИС) стоимость определяется площадью схемы на кристалле кремния и непосредственно не связана с числом микротранзисторов и других элементов. Нередко схема с большим числом элементов, но обладающая высокой регулярностью, занимает небольшую площадь, кроме того, она выгодна с точки зрения проектирования, ведь стоимость проектирования, как и стоимость изготовления, входит в суммарную стоимость устройства [28]. При построении устройства из дискретных компонентов в целях повышения надежности наряду с уменьшением их числа (что увеличивает вероятность безотказной работы) большое значение придается уменьшению числа соединений между компонентами (это также увеличивает вероятность безотказной работы). Кстати, эта задача решается на соответствующем графе – он разбивается на подграфы, минимально связанные между собой. Однако, для БИС надежность соединений внутри кристалла достаточно высока по сравнению с надежностью соединений между кристаллами. В связи с этим большое значение приобретает деление системы на БИС таким образом, чтобы уменьшить число точек соединений между ними.
Ограничимся в дальнейшем целью нахождения наиболее простого представления переключательной функции в смысле наименьшего числа входящих в нее символов (букв). Процесс получения такого представления будем называть минимизацией. Под различными символами (буквами) будем понимать вхождения одной и той же переменной в различные дизъюнктивные (конъюнктивные) члены функции. Так, функция z1(аbс)=аb Ú`aс Ú bс содержит шесть букв, а функция z2(аbс)=аb Ú`aс – четыре буквы, хотя обе функции зависят от трех переменных а,b,с (закон обобщенного склеивания z1=z2). Методы минимизации разрабатываются применительно к каждой отдельной функциональной полной системе элементных переключательных функций. Наиболее детально такие методы разработаны для систем из дизъюнкции, конъюнкции и инверсии. При этом задача минимизации переключательной функции сводится к нахождению такой ее формы, которая содержит наименьшее число дизъюнкций, конъюнкций и инверсий. Нахождение минимального представления функции в виде ДНФ или КНФ связано с решением двух основных задач [17]. Во-первых, это определение конъюнкций (дизъюнкций) входящих в ДНФ (КНФ), каждая из которых содержит минимальное число букв. Во-вторых, это определение ДНФ (КНФ), содержащей минимальное число различных элементарных конъюнкций (дизъюнкций). Будем рассматривать в основном минимизацию переключательных функций в классе ДНФ, не требуя минимизации числа инверсий.
8.2. Основные понятия и определения,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.215 (0.012 с.) |

 – некоторая переменная, причем символ ~ означает, что неважно, инверсная они или нет, т.е.
– некоторая переменная, причем символ ~ означает, что неважно, инверсная они или нет, т.е. 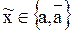 ; тогда
; тогда  .
. – некоторая функция, зависящая как от переменной х и ее инверсии
– некоторая функция, зависящая как от переменной х и ее инверсии  , так и от других переменных
, так и от других переменных  . Под одноименностью будем понимать и соответствие знаков инверсии (т.е. одновременное наличие или отсутствие). Тогда, если переменная
. Под одноименностью будем понимать и соответствие знаков инверсии (т.е. одновременное наличие или отсутствие). Тогда, если переменная  находится в конъюнкции с некоторой функцией, зависящей от данной переменной и от других переменных, то в этой функции все одноименные
находится в конъюнкции с некоторой функцией, зависящей от данной переменной и от других переменных, то в этой функции все одноименные 
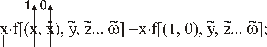


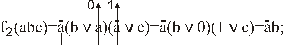
 и функции f соответствует их последовательное соединение. Такое соединение напоминает символ 1 (рис. 39). Для простоты на рис. 1 не указаны переменные функции f. Это значит, что одноименные переменные
и функции f соответствует их последовательное соединение. Такое соединение напоминает символ 1 (рис. 39). Для простоты на рис. 1 не указаны переменные функции f. Это значит, что одноименные переменные  в f заменяются на константу 0.
в f заменяются на константу 0.
 , инверсные одноименной, заменяются на константу 1. Сама же переменная остается без изменения:
, инверсные одноименной, заменяются на константу 1. Сама же переменная остается без изменения:
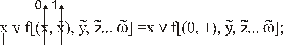
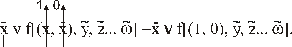


 . Поэтому обозначим аb, например, х:
. Поэтому обозначим аb, например, х:
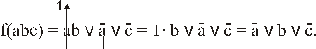









 и последующего применения формул равносильного преобразования:
и последующего применения формул равносильного преобразования: .
. Ú(
Ú( Úb)с[а
Úb)с[а 
 .
. =(fÚх)(fÚ
=(fÚх)(fÚ 
 .
.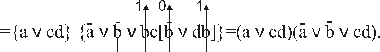
 содержащее множество попарно различных переменных или их инверсий, называется элементарной конъюнкцией (ЭК). Под
содержащее множество попарно различных переменных или их инверсий, называется элементарной конъюнкцией (ЭК). Под  понимается либо сама переменная х, либо ее инверсия
понимается либо сама переменная х, либо ее инверсия  =
= =
=  =
= =
=  .
. , т.е. это СДНФ.
, т.е. это СДНФ. 1=1). Если считать выражение z(аb) уравнением, то наборы 01, 10 – его решения.
1=1). Если считать выражение z(аb) уравнением, то наборы 01, 10 – его решения. . Таких переменных может быть несколько, будет несколько и тождественно истинных выражений. После этого раскрываются скобки и производятся необходимые упрощения.
. Таких переменных может быть несколько, будет несколько и тождественно истинных выражений. После этого раскрываются скобки и производятся необходимые упрощения.
 представим в виде: 00-Ú0-1.
представим в виде: 00-Ú0-1.
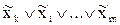 , содержащее множество попарно различных переменных или их инверсий, называется элементарной дизъюнкцией (ЭД).
, содержащее множество попарно различных переменных или их инверсий, называется элементарной дизъюнкцией (ЭД). ;
; (х1х2х3)=
(х1х2х3)=  =
= ;
; (х1х2х3)=
(х1х2х3)=  .
.



 .
. – на наборе 11.
– на наборе 11.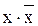 . Таких недостающих переменных может быть несколько; тогда надо добавлять соответствующие тождественно истинные выражения. Затем применяется распределительный закон и производятся необходимые упрощения.
. Таких недостающих переменных может быть несколько; тогда надо добавлять соответствующие тождественно истинные выражения. Затем применяется распределительный закон и производятся необходимые упрощения.