3.7. Мгновенным центром скоростей МЦС (иногда обозначают  ) называется такая точка плоской фигуры Ф, скорость которой в данный момент времени равняется нулю.
) называется такая точка плоской фигуры Ф, скорость которой в данный момент времени равняется нулю.
В случае движения тел произвольной формы МЦС отдельных тел может и не лежать в пределах тела, но обязательно лежит в плоскости движения тел.
3.8. Теорема. У плоской фигуры, совершающей плоскопараллельное (не поступательное) движение в каждый момент времени существует единственная точка  , скорость которой в данный момент времени равна нулю
, скорость которой в данный момент времени равна нулю  .
.

Доказательство. Пусть известны векторы скоростей двух точек фигуры  и
и  . Восстановим перпендикуляры в точках и найдем точку пересечения
. Восстановим перпендикуляры в точках и найдем точку пересечения  (рис. 3.12). Докажем, что скорость этой точки плоскости равна нулю
(рис. 3.12). Докажем, что скорость этой точки плоскости равна нулю  . Доказательство проведем методом от противного.Через точки
. Доказательство проведем методом от противного.Через точки  и
и  в направлении МЦС проведем две оси
в направлении МЦС проведем две оси  и
и  (рис.3.12 ). Воспользуемся теоремой о проекциях скоростей (3.12) для оси
(рис.3.12 ). Воспользуемся теоремой о проекциях скоростей (3.12) для оси  и найдем вектор скорости
и найдем вектор скорости  . По построению проекция вектора
. По построению проекция вектора  на ось
на ось  равна нулю, так как он перпендикулярен оси. Тогда и проекция вектора
равна нулю, так как он перпендикулярен оси. Тогда и проекция вектора  на эту ось равна нулю. Это возможно в двух случаях: или
на эту ось равна нулю. Это возможно в двух случаях: или  =0, или
=0, или  . Пусть скорость точки
. Пусть скорость точки  не равна нулю
не равна нулю 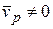 . Тогда
. Тогда  . Применяя теорему к точкам
. Применяя теорему к точкам  и
и  , приходим к выводу, что
, приходим к выводу, что  . Другими словами, приходим к противоречию. Одна точка в один и тот же момент времени не может двигаться в двух разных направлениях. Следовательно,
. Другими словами, приходим к противоречию. Одна точка в один и тот же момент времени не может двигаться в двух разных направлениях. Следовательно,  =0. Что и требовалось доказать. Отсюда следует правило построения МЦС.
=0. Что и требовалось доказать. Отсюда следует правило построения МЦС.
3.9.Чтобы построить мгновенный центр скоростей плоской фигуры  по известным векторам скоростей
по известным векторам скоростей  и
и  двух точек
двух точек  и
и  , надо в точках
, надо в точках  и
и  восстановить перпендикуляры к векторам скоростей и найти их точку пересечения
восстановить перпендикуляры к векторам скоростей и найти их точку пересечения  (рис. 3.11).
(рис. 3.11).
Чем же полезна точка, которую назвали мгновенным центром скоростей? Выберем точку  за полюс. Тогда скорость произвольной точки
за полюс. Тогда скорость произвольной точки  по формуле (3.7) примет вид:
по формуле (3.7) примет вид: 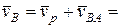
 , так как
, так как  =0.
=0.
3.10. Величину мгновенной скорости любой точки плоской фигуры, совершающей плоскопараллельное движение, можно вычислить по формуле (3.8), как произведение угловой скорости тела на расстояние от точки до мгновенного центра скоростей.
 ,
, 
 ,
,  . (3.14)
. (3.14)
Здесь 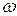 - угловая скорость фигуры при плоскопараллельном движении. Вектор скорости любой точки
- угловая скорость фигуры при плоскопараллельном движении. Вектор скорости любой точки  тела перпендикулярен к отрезку
тела перпендикулярен к отрезку 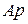 , соединяющему точку
, соединяющему точку  с мгновенным центром скоростей, и направлен в сторону вращения тела (по направлению круговой стрелки
с мгновенным центром скоростей, и направлен в сторону вращения тела (по направлению круговой стрелки 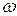 ). Формулы (3.14) позволяют по известной скорости точки и мгновенного центра скоростей определить угловую скорость фигуры.
). Формулы (3.14) позволяют по известной скорости точки и мгновенного центра скоростей определить угловую скорость фигуры.
 (3.15)
(3.15)
Сравнивая величины скоростей точек для одного и того же момента времени, то есть для одной и той же угловой скорости 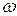 , из (3.14) имеем:
, из (3.14) имеем:
 (3.16)
(3.16)
Из (3.14) можно найти одну неизвестную величину, а другие три должны быть определены заранее.
Ниже приводятся примеры, иллюстрирующие некоторые правила и приемы определении МЦС.
Пример 3.3. Брус АВ движется в плоскости  опираясь точками А и В на две взаимно перпендикулярные идеально гладкие плоскости так, что его центр тяжести С приближается к горизонтальной оси Ох. Определить положение МЦС (точку р) бруса в показанный на рисунке момент времени.
опираясь точками А и В на две взаимно перпендикулярные идеально гладкие плоскости так, что его центр тяжести С приближается к горизонтальной оси Ох. Определить положение МЦС (точку р) бруса в показанный на рисунке момент времени.

Решение. Движение бруса ограничено связями в виде двух взаимно перпендикулярных абсолютно гладких плоскостей. По условию задачи сечение бруса плоскостью  , которое показано на рисунке, в процессе движения остается в плоскости
, которое показано на рисунке, в процессе движения остается в плоскости  . Следовательно, брус совершает плоскопараллельное движение. Известны траектории движения точек А и В – это оси Оу и Ох соответственно. Следовательно, траекториями точек являются прямые линии. Из кинематики точки знаем, что вектор скорости точки всегда направлен по касательной к траектории этой точки. Касательная к прямой линии совпадает с самой прямой. Так как траекториями точек А и В являются прямые, то можем утверждать, что векторы скорости
. Следовательно, брус совершает плоскопараллельное движение. Известны траектории движения точек А и В – это оси Оу и Ох соответственно. Следовательно, траекториями точек являются прямые линии. Из кинематики точки знаем, что вектор скорости точки всегда направлен по касательной к траектории этой точки. Касательная к прямой линии совпадает с самой прямой. Так как траекториями точек А и В являются прямые, то можем утверждать, что векторы скорости  и
и  «лежат» на осях Оу и Ох соответственно. Но в какую сторону они направлены? По условию задачи точка С перемещается вниз. Поскольку брус является абсолютно твердым телом, то повседневный опыт подсказывает, что точка А тоже перемещается вниз. Поэтому вектор перемещения точки А, не показанный на рисунке, направлен строго вниз. Вектор скорости точки при любом характере движения сонаправлен с вектором перемещения, а для прямолинейных траекторий их направления просто совпадают (см. главу 1). Следовательно, вектор скорости
«лежат» на осях Оу и Ох соответственно. Но в какую сторону они направлены? По условию задачи точка С перемещается вниз. Поскольку брус является абсолютно твердым телом, то повседневный опыт подсказывает, что точка А тоже перемещается вниз. Поэтому вектор перемещения точки А, не показанный на рисунке, направлен строго вниз. Вектор скорости точки при любом характере движения сонаправлен с вектором перемещения, а для прямолинейных траекторий их направления просто совпадают (см. главу 1). Следовательно, вектор скорости  направлен вниз, как показано на рисунке.
направлен вниз, как показано на рисунке.
Направление вектора скорости  в данной задаче можно найти интуитивно, но это бывает невозможно сделать в более сложных задачах. Поэтому воспользуемся теоремой 3.5 о проекциях скоростей двух точек на ось, проходящую через эти точки, считая направление вектора
в данной задаче можно найти интуитивно, но это бывает невозможно сделать в более сложных задачах. Поэтому воспользуемся теоремой 3.5 о проекциях скоростей двух точек на ось, проходящую через эти точки, считая направление вектора  установленным. Проекции векторов
установленным. Проекции векторов  и
и  на ось, проходящую через точки А и В будут равны, если вектор
на ось, проходящую через точки А и В будут равны, если вектор  направить по траектории движения вправо, как показано на рисунке (см. еще пример 3.2). Чтобы найти МЦС теперь достаточно по правилу 3.9 восстановить перпендикуляры в точках А и В и найти точку их пересечения
направить по траектории движения вправо, как показано на рисунке (см. еще пример 3.2). Чтобы найти МЦС теперь достаточно по правилу 3.9 восстановить перпендикуляры в точках А и В и найти точку их пересечения  . Итак, брус АВ совершает мгновенно вращательное движение против часовой стрелки относительно точки
. Итак, брус АВ совершает мгновенно вращательное движение против часовой стрелки относительно точки  .
.
Пример 3.4. Линейка эллипсографа приводится в движение кривошипом  . Определить положение мгновенного центра скоростей линейки в показанном на рисунке положении.
. Определить положение мгновенного центра скоростей линейки в показанном на рисунке положении.
Решение. В этом примере известны траектории движения трех точек линейки- точек  . Вектор скорости точки
. Вектор скорости точки 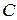 перпендикулярен к
перпендикулярен к  и направлен по направлению вращения кривошипа – по направлению
и направлен по направлению вращения кривошипа – по направлению  . Траектории точек
. Траектории точек  - прямые, что навязано конструкцией механизма (связями-ползунами). Зная направление вектора
- прямые, что навязано конструкцией механизма (связями-ползунами). Зная направление вектора  , по теореме о проекциях скоростей получаем направления векторов
, по теореме о проекциях скоростей получаем направления векторов  . По правилу 3.9 положение получаем положение точки
. По правилу 3.9 положение получаем положение точки  , направление угловой скорости
, направление угловой скорости 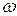 и направление мгновенного вращения линейки эллипсографа.
и направление мгновенного вращения линейки эллипсографа.

Пример 3.5. Брус АВ движется в плоскости  опираясь точками А и В на две взаимно перпендикулярные идеально гладкие плоскости так, что его центр тяжести С приближается к горизонтальной оси Ох. Одна из плоскостей вырождается в точку
опираясь точками А и В на две взаимно перпендикулярные идеально гладкие плоскости так, что его центр тяжести С приближается к горизонтальной оси Ох. Одна из плоскостей вырождается в точку  . Определить положение МЦС (точку р) бруса в показанный на рисунке момент времени.
. Определить положение МЦС (точку р) бруса в показанный на рисунке момент времени.
Решение. Мгновенный центр скоростей определяется как в примере 3.3, но требуетпояснения определение направления вектора скорости  точки
точки  бруса, показанное на рис. к примеру. Если взять за тело отсчета брус, то вектор скорости угла
бруса, показанное на рис. к примеру. Если взять за тело отсчета брус, то вектор скорости угла  будет направлен по касательной к его траектории, то есть по краю бруса вверх. Следовательно, точки самого бруса, касающиеся неподвижного угла, имеют вектора скоростей, направленные по краю бруса вниз, как показано на рисунке. Положение точки
будет направлен по касательной к его траектории, то есть по краю бруса вверх. Следовательно, точки самого бруса, касающиеся неподвижного угла, имеют вектора скоростей, направленные по краю бруса вниз, как показано на рисунке. Положение точки  определяется из геометрических построений по правилу 3.9.
определяется из геометрических построений по правилу 3.9.
Пример 3.6. Кривошипно-шатунный механизм с известными длинами кривошипа и шатуна приводится в движение вращением кривошипа  и совершает плоское движение. В точке
и совершает плоское движение. В точке  ползун с осью, совпадающей с осью координат
ползун с осью, совпадающей с осью координат  . В показанном на рисунке положении механизма, определить положение мгновенного центра скоростей шатуна
. В показанном на рисунке положении механизма, определить положение мгновенного центра скоростей шатуна  .
.
Решение. Определим направление вектора скорости точки  . Точка принадлежит вращающемуся кривошипу
. Точка принадлежит вращающемуся кривошипу  , поэтому (см.гл.2) вектор скорости перпендикулярен радиусу
, поэтому (см.гл.2) вектор скорости перпендикулярен радиусу  и направлен в сторону вращения – по направлению дуговой стрелки
и направлен в сторону вращения – по направлению дуговой стрелки 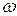 . Интересно отметить, что
. Интересно отметить, что  , и точка
, и точка  является для кривошипа не мгновенным, а просто центром вращения. Точка
является для кривошипа не мгновенным, а просто центром вращения. Точка  - общая для кривошипа и шатуна, и оба тела в этой точке имеют одну и ту же скорость. Вектор скорости точки
- общая для кривошипа и шатуна, и оба тела в этой точке имеют одну и ту же скорость. Вектор скорости точки  должен лежать на оси
должен лежать на оси  . Это навязано связью – ползуном. Применяя терему 3.5 о проекциях скоростей, определяем истинное направление вектора
. Это навязано связью – ползуном. Применяя терему 3.5 о проекциях скоростей, определяем истинное направление вектора  , показанное на рисунке. Положение мгновенного центра скоростей шатуна
, показанное на рисунке. Положение мгновенного центра скоростей шатуна  определяется теперь элементарно по правилу 3.9. Итак, механизм совершает плоское движение. Но при этом, кривошип совершает вращательное движение относительно оси, проходящей через точку
определяется теперь элементарно по правилу 3.9. Итак, механизм совершает плоское движение. Но при этом, кривошип совершает вращательное движение относительно оси, проходящей через точку  , перпендикулярно к плоскости рисунка, а шатун
, перпендикулярно к плоскости рисунка, а шатун  в данный момент времени совершает мгновенно вращательное движение относительно оси, проходящей через точку
в данный момент времени совершает мгновенно вращательное движение относительно оси, проходящей через точку  , перпендикулярно плоскости рисунка.
, перпендикулярно плоскости рисунка.


 ) называется такая точка плоской фигуры Ф, скорость которой в данный момент времени равняется нулю.
) называется такая точка плоской фигуры Ф, скорость которой в данный момент времени равняется нулю. .
.
 и
и  . Восстановим перпендикуляры в точках и найдем точку пересечения
. Восстановим перпендикуляры в точках и найдем точку пересечения  . Доказательство проведем методом от противного.Через точки
. Доказательство проведем методом от противного.Через точки  и
и  в направлении МЦС проведем две оси
в направлении МЦС проведем две оси  и
и  (рис.3.12 ). Воспользуемся теоремой о проекциях скоростей (3.12) для оси
(рис.3.12 ). Воспользуемся теоремой о проекциях скоростей (3.12) для оси  . По построению проекция вектора
. По построению проекция вектора  на эту ось равна нулю. Это возможно в двух случаях: или
на эту ось равна нулю. Это возможно в двух случаях: или  . Пусть скорость точки
. Пусть скорость точки 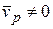 . Тогда
. Тогда  . Применяя теорему к точкам
. Применяя теорему к точкам  . Другими словами, приходим к противоречию. Одна точка в один и тот же момент времени не может двигаться в двух разных направлениях. Следовательно,
. Другими словами, приходим к противоречию. Одна точка в один и тот же момент времени не может двигаться в двух разных направлениях. Следовательно,  по известным векторам скоростей
по известным векторам скоростей 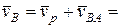
 , так как
, так как  ,
, 
 ,
,  . (3.14)
. (3.14)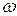 - угловая скорость фигуры при плоскопараллельном движении. Вектор скорости любой точки
- угловая скорость фигуры при плоскопараллельном движении. Вектор скорости любой точки 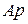 , соединяющему точку
, соединяющему точку  (3.15)
(3.15) (3.16)
(3.16) опираясь точками А и В на две взаимно перпендикулярные идеально гладкие плоскости так, что его центр тяжести С приближается к горизонтальной оси Ох. Определить положение МЦС (точку р) бруса в показанный на рисунке момент времени.
опираясь точками А и В на две взаимно перпендикулярные идеально гладкие плоскости так, что его центр тяжести С приближается к горизонтальной оси Ох. Определить положение МЦС (точку р) бруса в показанный на рисунке момент времени.
 . Определить положение мгновенного центра скоростей линейки в показанном на рисунке положении.
. Определить положение мгновенного центра скоростей линейки в показанном на рисунке положении. . Вектор скорости точки
. Вектор скорости точки 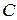 перпендикулярен к
перпендикулярен к  . Траектории точек
. Траектории точек  - прямые, что навязано конструкцией механизма (связями-ползунами). Зная направление вектора
- прямые, что навязано конструкцией механизма (связями-ползунами). Зная направление вектора  , по теореме о проекциях скоростей получаем направления векторов
, по теореме о проекциях скоростей получаем направления векторов  . По правилу 3.9 положение получаем положение точки
. По правилу 3.9 положение получаем положение точки 
 точки
точки  и совершает плоское движение. В точке
и совершает плоское движение. В точке  . В показанном на рисунке положении механизма, определить положение мгновенного центра скоростей шатуна
. В показанном на рисунке положении механизма, определить положение мгновенного центра скоростей шатуна  .
. , и точка
, и точка  является для кривошипа не мгновенным, а просто центром вращения. Точка
является для кривошипа не мгновенным, а просто центром вращения. Точка  , показанное на рисунке. Положение мгновенного центра скоростей шатуна
, показанное на рисунке. Положение мгновенного центра скоростей шатуна 


